陈海飞

[摘 要]“找次品”是人教版教材五年级下册数学广角的内容,和“打电话”一样,属于解题策略和方案优化问题,这类问题具有强烈而明显的操作性和实践性,需要通过实践探究总结出一般策略,进而建立一般的解题模型。
[关键词]找次品;轻重;至少;次数;分组
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)32-0029-02
有一篇论文(以下称“论文A”)分析了一道关于找次品的练习题:“一批产品共有6件,其中1件是次品,从外观上无法分辨,只有质量略有差异,如何找出次品?用天平称,至少称几次能确保找出次品?”并提出“一般通过分一分、称一称、找一找三个步骤,至少称4次能确保找出次品”。文章作者还引导学生大胆猜想“正常情况下,如果提前告知次品是重于或轻于正品,产品数量介于3[n-1]与3[n]之间,能确保找出次品的最少称量次数就是n”,并在后文中验证了这个猜想,形成结论。
一、观点对撞
而另一篇论文(以下称“论文B”)则对论文A的结论予以驳斥,它不仅以检测有1件次品的4件产品为例来反驳,还以有1件次品的14件产品为例,详述了在不知道次品与正品谁轻谁重的前提下,找出次品的一般流程。按论文B的论述,当产品数量为14时,至少称5次才可以确保找出次品。论文B还论证了3~76件产品找次品(不知次品与正品谁轻谁重)的检测流程,并归纳出一般公式:当产品数量大于6时,产品数量与找出次品所需的最少称量次数存在这样的数量关系:当2[n-1]< [产品数量-49] <[2n]时,能确保找出次品的最少称量次数是(n+4)次。
例如:在不知道次品与正品谁轻谁重时,如果产品数量为9,由于[9-49] = [59],2[-1]< [59] <[20],0+4=4,那幺能确保找出次品的最少称量次数是4;如果产品数量为14,由于[14-49] = [109],2[0] <[109] <[21],1+4=5,那幺能确保找出次品的最少称量次数为5。
笔者对论文B的结论持保留意见。下面,笔者同样以14件产品为例来阐述个人意见。笔者的操作方法是:
首先把14件产品随机编号为1~14,然后按照编号分成三组:a1组为1~5号,b1组为6~10号,c1组为11~14号。第一次称a1、b1两组,可能出现两种结果。
(1)天平平衡。那幺次品在c1组中,第二次可以称11号和12号,也可能有两种结果。①天平平衡,则次品必然是13号或14号。第三次可以称11号(已证实为正品)和13号,若天平平衡,则次品是14号;若天平倾斜,则次品是13号。②天平倾斜,则次品不是11号就是12号,13号和14号必为正品。第三次可以称11号和13号,若天平平衡,则次品必是12号;若天平倾斜,则11号为次品。
(2)天平倾斜。则次品在a1、b1两组的某一组中,不妨将这两组产品混合,再分为(3,3,4)三组,第二次称(3,3)两组,也可能有两种结果。①天平平衡,则次品在“4”组中,按4件产品找次品的步骤,至少称2次能确保找出次品。因此,至少要称4次。②天平倾斜(假设左“3”组重于右“3”组),则次品必然在这两组中,第三次则可在“4”组中取出3件产品与左“3”组对比称量。若天平平衡,则次品必然在右“3”组中,同时可以推知次品偏轻,那幺第四次可在右“3”组中任取2件产品对比称量,若天平平衡,则没放到天平上的那件为次品;若天平倾斜,则较轻的那件是次品。若天平倾斜,则次品在左“3”组中,同时推知次品重于正品,那幺第四次可在左“3”组中任取2件对比称量,若天平平衡,则次品是没放到天平上的那件;若天平倾斜,则较重那件是次品。
二、操作验证
通过上述操作方法可知,当产品数量为14时,至少称4次即可确保找出次品,并非论文B中所说的5次。由此可见,论文B也有漏洞。那幺在一批产品中,当不知次品比正品轻还是重时(只含1件次品),如何尽快找出它呢?笔者以为仍需降低层级,从最简单的情况开始考虑。为叙述方便,设产品数量为n,依次编号为1~n,按照编号分为a2、b2、c2三组。
1.当产品数量为3时,需称2次。操作如下:
第一次,称1号和2号。(1)天平平衡,则3号必然是次品。(2)天平倾斜,则第二次称1号和3号(确认为正品),若天平平衡,则2号是次品;若天平倾斜,则1号是次品。
2.当产品数量为4时,至少称2次。操作如下:
第一次,称1号和2号。(1)天平平衡,则次品为3号或4号,第二次称1号和3号。若天平平衡,则可以确定4号为次品;若天平倾斜,则3号定为次品。(2)天平倾斜,则次品为1号或2号,第二次称1号和3号,若天平平衡,则可推知2号为次品;若天平倾斜,则1号为次品。
3.当产品数量为5时,至少称3次。操作如下:
把5件产品分成(2,2,1)三组,先称(2,2)两组。(1)天平平衡,则直接确认5号是次品。(2)天平倾斜,则次品在(2,2)两组中,再按4件产品找次品的步骤来处理,至少还需称2次,一共是3次。
4.当产品数量为6时,至少称3次。操作如下:
把6件产品分成(2,2,2)三组,然后称前(2,2)两组。(1)天平平衡,则判断次品为5号或6号。再称1号和5号,若天平平衡,则判断6号为次品;若天平倾斜,则5号为次品。(2)天平倾斜,则次品在前(2,2)两组中,再按4件产品找次品的步骤操作,至少还需称2次,一共是3次。
5.当产品数量为7~10时,也至少需称3次。具体操作略。
这也说明,论文B中,产品数量为9时至少称4次才能确保找到次品的结论是错误的。
三、原理探索
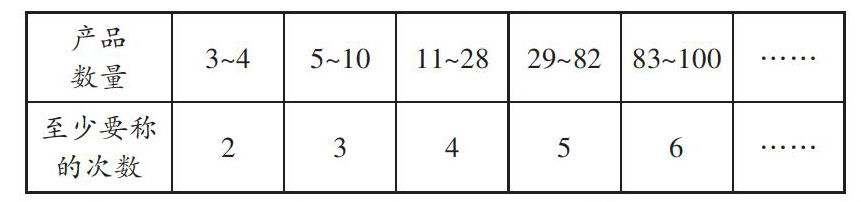
笔者通过大量操作验证得出一组实验数据。
从上表可以看出,当产品数量大于2,且不知道次品与正品谁轻谁重时,产品数量与确保找到次品至少要称的次数存在这样的数量关系:当[3n]+1<产品数量≤[3n+1]+ 1时,至少称(n+2)次可以保证找到次品。例如当产品数量为4时,由于[30]+1<4≤[31]+ 1,即n =0,所以至少要称0+2=2(次)。又如当产品数量为14时,由于[32]+1<14≤[33]+ 1,即n=2,所以至少要称2+2=4(次)。
笔者在操作实践后发现,在不知次品与正品谁轻谁重时,为了尽快找出次品,分组很关键,分组和操作时应遵循如下原则:
一是尽量将产品平分成三组(a、b、c),如果实在无法平分成三组,至少要保证其中两组(a组与b组)的产品数量相等,且c组的产品数量与它们的相差1,第一次称时选择a、b两组。
二是当[3n]+1<产品数量≤[3n+1]+1时,a(b)组的产品数量≤[3n],且c组的产品数量≤[3n]+1。例如当产品数量是5~10时,由于[31]+1<产品数量≤[31+1]+1,即n =1,所以a、b两组的产品数量不超过3([31]),同时c组的产品数量不超过4([31]+1),这样首次称量时,若天平平衡,则次品范围可以缩小到c组中。由于c组的产品数量≤[3n]+ 1,所以至少称(n + 1)次即可找出次品。还是以产品数量是5~10时为例,由于 [31]+1<产品数量≤[31+1]+ 1,即n=1,所以a、b两组的产品数量不多于3([31]),同时c组的产品数量不超过4([31]+1)。
当称a、b两组时,若天平平衡,那幺次品可以锁定在c组中,因为c组的产品数量不超过4,所以找出次品要称的次数不超过2次,总次数也不超过3次。
三是考虑到如果首次称量时天平倾斜,则次品在a、b两组中,所以在分组时还应考虑到二次称量后确定次品所在组别,同时还应能够判断出次品是轻于还是重于正品。例如产品数量为70时,若分成(20,20,30)三组,当(20,20)组平衡时,次品在30件组中。由于30>28,根据前述理论可知,在不知道次品是轻于还是重于正品的情况下,30件产品无法称4次保证找到次品;若分成(25,25,20)三组时,在称(25,25)组倾斜后,锁定次品在这两组产品共50件中,第二次无论怎幺称,既无法确定次品在a组还是在b组,也无法获知次品是轻于还是重于正品,这样对于50件产品,同样无法保证在4次称量内找出次品。而如果分成(21,21,28)三组,若天平平衡,则次品在c组的28件产品中,按前述理论称4次即可找出次品;若天平倾斜,则次品在a、b两组的某一组中,记住a、b倾斜的情况,第二次在c组中取21件产品与a组对比称量,即可判断出次品所在组别,并确定次品是轻于还是重于正品,按理论已知次品轻或重于正品的前提下,21件产品只需称3次即可找出次品,共5次即可找出次品。根据上述原则,分成(22,22,26)三组或(23,23,24)三组,同样称5次即可保证找出次品。
(责编 吴美玲)



