吴荣


摘 要:几何是初中数学的重难点,是学生普遍存在学习困难之处,因此几何教学显得格外重要.本文通过对教材的深入探究,提炼几何模型,采用模型解题法提升学生的解题效率,强化学生的思维.
关键词:三垂直全等模型;本质;添补;模型思想
教材是教学内容的根本,也是编制各类试题的材料来源.教材里的例题或习题具有经典性、示范性、导向性,教师要重视对教材中的例题或习题所蕴含的知识、思想方法的挖掘和研究,对教材内容的具体化和进一步拓展,这也是探究知识的本质属性和编制试题的重要途径.下面以一道苏科版八年级上册第一章《全等三角形》“复习巩固”里的习题为例,具体探究习题背后所隐含的几何模型与思想方法.
已知:如图1,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S,N,Q,且MS=PS.求证:△MNS≌△SQP.
如上图,将直线BD绕直角顶点B旋转,当直线BD穿过等腰直角三角形内部时,如图2.当直线BD旋转到等腰三角形外部时,如图3.这就是一线三垂直全等模型的两种基本图形.
用符号语言表述为:已知∠ABC=∠AEB=∠BDC=90°,AB=BC.
结论:Rt△ABE≌Rt△BCD.
从上面的图形可以清楚地看出该模型的本质特征是过等腰直角三角形的直角顶点的一条直线,无论该直线如何旋转,从两个底角顶点向该直线作垂线段,所构成的两个直角三角形总是全等的.把握其本质,才能合理地构建模型,运用模型,从模型中提取三角形全等关系.
2 补全模型,变式应用
一线三垂直全等模型虽然有着较高的识别度,但是试题中提供的图形往往是不规整的,是错综复杂的,甚至将模型的局部隐藏起来,需要学生运用恰当的方法作辅助线,对图形进行添补,使模型显现出来,这对学生的图形识别能力、推理和抽象能力要求较高.下面就一些实例进行探究.
2.1 一角隐藏,垂线添补
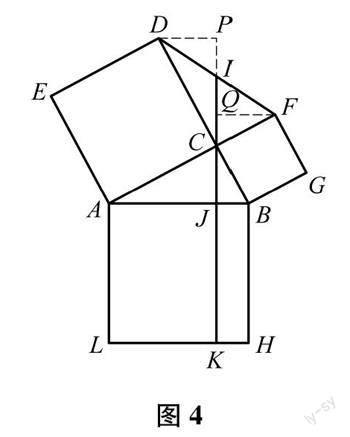
例1 (2022年武汉市中考题)如图4,在Rt△ABC中,∠ACB=90°,AC>BC,分别以△ABC的三边为边向外作三个正形ABHL,ACDE,BCFG,连接DF.过点C作AB的垂线CJ,垂足为J.分别交DF,LH于点I,K.若CI=5,CJ=4,则四边形AJKL的面积是 .
分析:本题的图形是由三个正方形和两个直角三角形组成的,故存在多组相等的边和直角,又因为已知长度的两条线段均过直角顶点,故以此为切入点,通过作两条辅助线——垂线,可以构建两个一线三垂直全等模型,如模型图3所示,从而借助全等三角形实现线段长度关系的转移,进而求出矩形AJKL的面积.
上述的图形中两处都存在“一线两直角”的情形,通过作辅助线——作垂线和线段延长线,即可补上一个直角构造三垂直全等模型.对模型的构建过程源于对模型的深刻理解和灵活运用能力,从中培养学生用模型解题的思想和意识.
上述问题的解题突破口在于把握其中的直角,过该直角顶点补上一条垂线,这是构造三垂直全等模型的关键一步.依托于特殊角,经过合理地联想,探寻图形之间的联系来构建几何模型,有利于培养学生的模型思想、推理能力、几何直观能力.
2.3 线角全藏,作图补型
例3 在平面直角坐标系中,A(0,3),点B的纵坐标为2,点C的纵坐标为0,当A、B、C三点围成等腰直角三角形时,求点B、C的坐标.
分析:本题没有已知图形,而且没有明确指出A、B、C三点围成的等腰直角三角形哪个角是直角,因此需要分类讨论A、B、C分别为直角顶点的情形.依照不同的直角顶点所构造的三垂直模型截然不同,需要具体情况具体分析.
解:① 当A为直角顶点,B在第一象限,C在x轴负半轴时,如图6,根据三垂直全等模型可知△ABH≌△CAO,从而可求B(3,2),C(-1,0);
在以直角坐标系为背景的几何问题中,当出现等腰直角三角形或是正方形时,往往也存在着三垂直全等模型.由于直角坐标系的特殊性,构造三垂直全等模型时一般是依托x轴或y轴,以及平行于x轴或y轴的直线来作辅助线的.如本题中的图6图9所构造的三垂直全等模型都是基本模型图2的衍生图,过等腰直角三角形的直角顶点的一条直线穿过了等腰直角三角形的内部.图10、图11则是基本模型图3的衍生图,该直线不穿过等腰直角三角形的内部.这类试题涵盖的知识点较多,综合性强,要充分挖掘题目条件,把握好分类的标准,才能做到条理清晰,有理有据,从而合理地构建模型具体求解.对问题的深入分析可以有效地促进学生思维能力的提升,以及数学素养的培养.
3 解后反思,教学建议
从上述的解题过程中可以看出一线三垂直全等模型并不都是直观地、完整地呈现出来的,需要学习者在对模型及其衍生图的深度理解和充分掌握的基础上,在反复的解题训练和积累中练就一双“火眼金睛”,将拥有“七十二变”的几何图形看穿、看透,揪出几何模型的点点蛛丝马迹——直角,并以此为基础,作辅助垂线来补全模型.
在教学中,教师首先要深挖教材,提炼几何模型,培养学生运用模型思想解题的能力.几何是初中的重难点内容,教师要以教材为蓝本,深入挖掘教材中的例题和习题,将一些有共性的图形分离出来成为经典的、有代表性的、结构相对简单的几何模型,在解题教学中围绕着几何模型展开,让学生在面对千变万化的题型和复杂的图形时,有法可依,即紧扣基本模型,运用模型思想来解题,使学生易于着手,易于理解和接受,让学生体验成功解题的愉悦感,增强学生的识图能力和几何直观能力.
其次是把握几何模型的本质特征,提升模型的构建能力.每个模型有着其鲜明的几何特征,只有深刻理解和把握其本质的特征,才能在复杂的图形中识别到模型的影子,才能合理地构建和熟练自如地运用.如一线三垂直全等模型是以等腰直角三角形或正方形为背景的,无论过直角顶点的直线如何运动变化,总能通过作垂线构建一组全等三角形.其本质是得到三角形的全等关系.引导学生抓住模型的本质属性,提升模型识别和构建的能力,总结解题的方法策略,养成运用模型解题的习惯.
最后是关注学生解题的过程和存在的问题,提高学生的解题效率.运用几何模型解题的基本思路是找角、定线、建模,解题的过程是学生思维方式具体展现的过程,教师要关注学生的解题思路的形成过程和存在的问题,以此为切入点,帮助学生分析问题存在的根源,是对模型的认识不够深刻,还是基础知识的欠缺,或是综合能力不够、思维容易混乱;分析数形结合思想、模型思想和方法是如何具体应用的,理顺解题的步骤,并注意融会贯通,以一题会一类,形成解题通法,从而提升学生的解题效率.
总之,在几何教学中,对教材的深挖,对几何模型的提炼是对问题本质的探寻和把握.利用几何模型展开解题教学,让学生在多组题型中进行纵横比较,可以提升学生思维能力,培养学生数学建模的思想,促进学生核心素养的发展.
参考文献:
[1] 王琼.分析几何结构提炼基本模型[J].中学数学教学参考,2022(36):4547.
[2] 汤久妹,曹亦祥.几何教学要重视“模型”的提炼和运用——一道中考题引起的思考[J].初中数学教与学,2015(12):1113.



