李芃杉
(河北省衡水第一中学 053000)
不等式中的恒成立存在性问题是近年来考题的热点和难点,经常在各种联考试卷和高考试卷上出现,这类试题要求学生要有扎实的函数知识和不等式知识,要有较强的逻辑推理能力、严谨的思维习惯及对数学思想方法的正确认识和把握,学生往往感到无从下手,因而得分率极低.本文从一些考题出发,给出这类问题的“解法模式”.
基本结论1 设函数f(x)在区间D上有定义,常数a
(1)∀x∈D,f(x)≥a恒成立⟺f(x)min≥a;(2)∀x∈D,f(x)≤a恒成立⟺f(x)max≤a;(3)∃x∈D,使得f(x)≥a⟺f(x)max≥a;(4)∃x∈D,使得f(x)≤a⟺f(x)min≤a.
例1 当x∈(1,2)时,不等式x2+mx+4<0恒成立,则m的取值范围是____.
分析设函数f(x)=x2+mx+4,由题意得f(x)<0恒成立,即f(x)min<0.但这样解决问题变复杂了,因为f(x)min的求解是“动轴定区间”问题,需要分类讨论.所以对于这类问题我们首选“分离常数”.
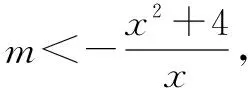
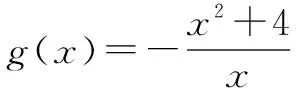
基本结论2 设函数f(x)和g(x)在区间D上都有定义,且∀x∈D.
(1)f(x)≤g(x)⟺f(x)-g(x)≤0⟺(f(x)-g(x))max≤0;(2)f(x)≥g(x)⟺f(x)-g(x)≥0⟺(f(x)-g(x))min≥0.
例2 当a≥0,x>1时,求证x>ln2x-2alnx+1.
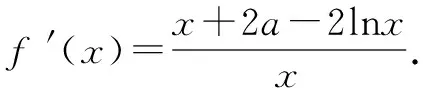
基本结论3 设函数f(x)在区间D1上有意义,g(x)在区间D2上有意义.
(1)∀x1∈D1,∃x2∈D2,f(x1)≥g(x2)⟺f(x1)min≥g(x2)min;
(2)∀x1∈D1,∀x2∈D2,f(x1)≥g(x2)⟺f(x1)min≥g(x2)max;
(3)∃x1∈D1,∀x2∈D2,f(x1)≥g(x2)⟺f(x1)max≥g(x2)max;
(4)∃x1∈D1,∃x2∈D2,f(x1)≥g(x2)⟺f(x1)max≥g(x2)min.
对于双变元的分析可以分步转化.如:∀x1∈D1,∃x2∈D2,f(x1)≥g(x2),可以先把x1作为变元,把f(x2)当作常数a,问题转化为∀x1∈D1,f(x1)≥a,所以f(x1)min≥a.然后把f(x1)min当作常数b,再把问题转化为∃x2∈D2,b≥g(x2),所以b≥g(x2)min,从而得到∀x1∈D1,∃x2∈D2,f(x1)≥g(x2)⟺f(x1)min≥g(x2)min.
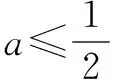
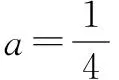
分析(2) 任意的x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则f(x1)min≥g(x2)min.
解(1)利用导数与分类讨论,容易得到:
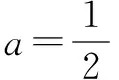
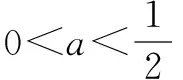
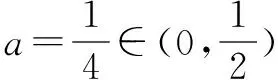
又g(x)=x2-2bx+4=(x-b)2+4-b2x∈[1,2] ,所以当b<1时,
g(x)min=g(1)=5-2b>0与(*)矛盾;当b∈[1,2]时,g(x)min=g(1)=4-b2≥0与(*)矛盾;当b∈(2,+)时,g(x)min=g(2)=8-4b,解不等式得综上,实数b的取值范围是) .
不等式的恒成立存在性问题多与参数的取值范围问题联系在一起,它以“参数处理”为主要特征,以“导数”为主要解题工具.这类问题往往与函数的最值有关,所以解题时要善于将这类问题与函数最值联系起来,通过函数最值求解相关问题.虽然不等式恒成立存在性问题涉及知识面广,解题方法灵活多样,技巧性强,难度大,要求有较强的思维灵活性和创造性、较高的解题能力,但也不是没有规律可寻的.“模式识别、差异分析”是我们解决高中数学问题的基本途径,因此必须先掌握上述“基本模式”,解题时通过分析把问题转化为固定模式求解.



