何正文
(广东省肇庆市百花中学 526000)
一道题可以因为有思考角度,解题顺序,定理公式运用,数学公式变式,代入方式,知识板块不同而多解.下面从六个例子的不同解法中剖析出其中的本质.
一、 运用思考角度不同的一题多解
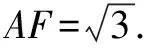
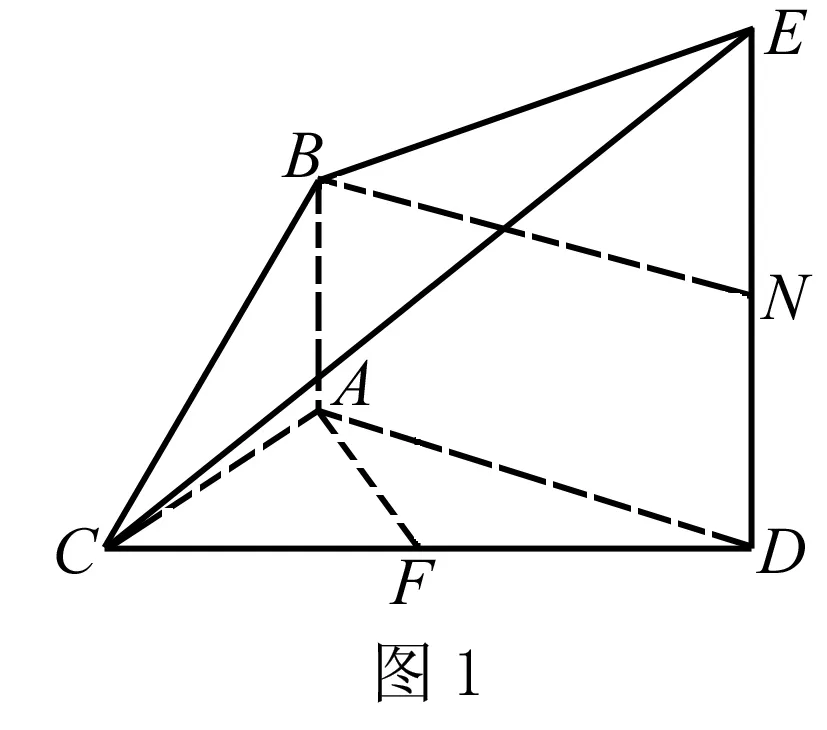
这道题解法用多面体的体积知识点做,从分割,补全,不割不补的不同思考角度有不同的解法.
从把原多面体分割成三个小几何体这个角度出发:
解法一取CE中点M,ED中点N,则可将此多面体分割成三个小几何体,分别是四棱锥C-ABMF,三棱柱BMN-AFD以及三棱锥E-BMN,CD=2.
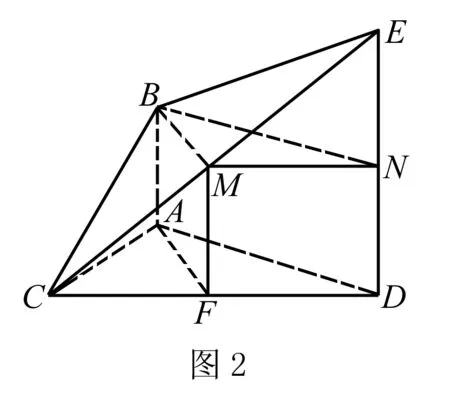
通过证明和计算,可以得到:CD⊥面ABMF,BA⊥面ACD,EN⊥面BMN,CD=2.
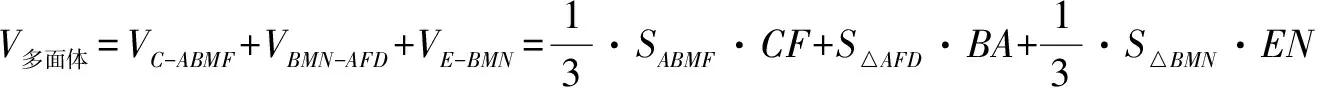
从把原多面体补全成一个大几何体这个角度出发:
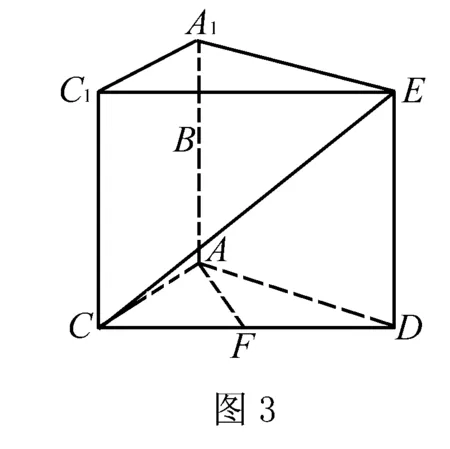
解法二把原几何体补全成一个新的几何体(三棱柱ACD-A1C1E)发现,原多面体的体积是三棱柱ACD-A1C1E体积的一半.
从对原多面体既不分割也不补全这个角度出发:
解法三(对原多面体既不分割也不补全)
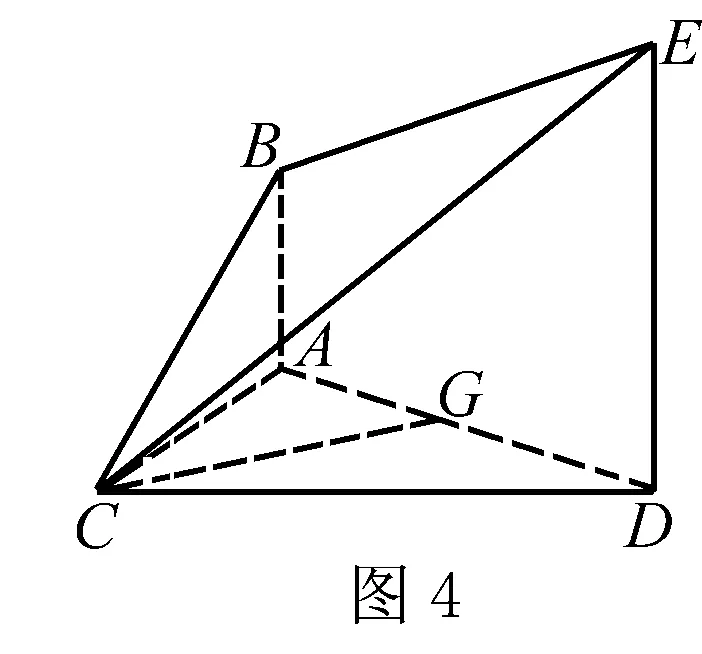
把原多面体看成一个以C为顶点,四边形ABED为底面的四棱锥.
过C作CG⊥AD,通过证明可知:CG⊥面ABED.
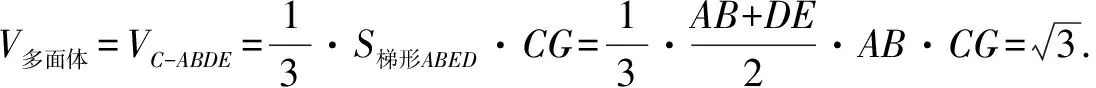
二、解题顺序不同的一题多解
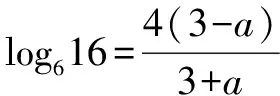
证法一(从左到右)
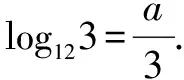
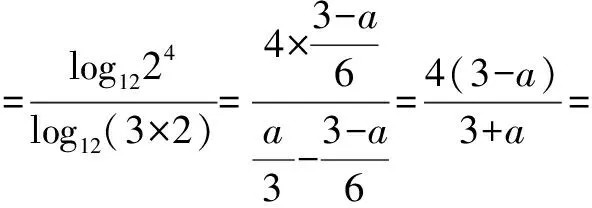
证法二(从右到左)
∵log1227=a,

证法三(中间会师)
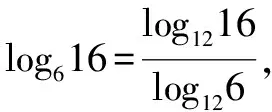
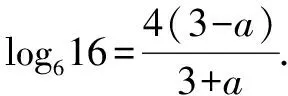
证法四(转化条件)
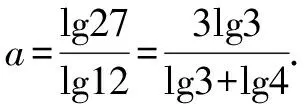
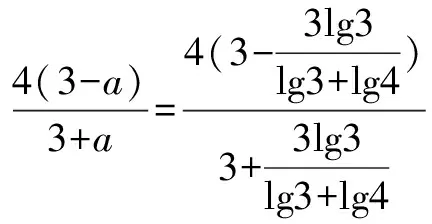
以上一题多解,既可看到知识的内在联系、巧妙转化和灵活运用,又可梳理推理论证等式的一般方法和思路:从左到右、从右到左、中间会师、转化条件等,这些对提高解题能力是多幺重要.
三、运用定理公式不同的一题多解

这道题解法都是用角和边互换的知识做,分别用余弦定理,正弦定理,射影定理,有不同的解法.
从余弦定理这个知识点出发:
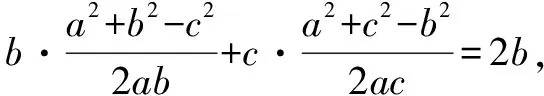
从正弦定理这个知识点出发:
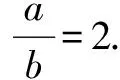
从射影定理这个知识点出发:
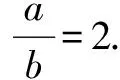
四、运用数学公式变式不同的一题多解
例4 已知抛物线在y轴上的截距为3,对称轴为直线x=-1,在x轴上截得线段长为4,求抛物线方程.
这道题是考察抛物线公式的知识点,我们可以选取不同的抛物线公式,有不同解法.
从抛物线方程的一般式:
解法一截距为3,可选择一般式方程:y=ax2+bx+c(a≠0).
显然有c=3,利用其他条件可列方程组求a,b值.
从抛物线方程的顶点式:
解法二由对称轴为直线x=-1,可选择顶点式方程:
y=a(x-m)2+k(a≠0).
显然有m=-1,利用其他条件可列方程组求a,k的值.
从抛物线方程的两根式:
解法三由一元二次方程与一元二次函数关系可选择两根式
y=a(x-x1)(x-x2)(a≠0)(必须与x轴有交点).
显然x1=-3,x2=1.由截距3,可求a值.
五﹑运用代入方式不同的一题多解
例5 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=1,则f(-3)等于( ).
A.2 B.3 C.6 D.9
这道题是代入法来做,我们可以选取不同的代入值,有不同解法.
解法一f(x+y)=f(x)+f(y) 中,可令x,y特殊值,计算出前几项,猜想出结果.令x=0,y=0, 得f(0)=0;令x=1,y=1, 得f(2)=4;再令x=1,y=2, 得f(3)=9.则f(0)=0,f(1)=1,f(2)=4,f(3)=9猜想f(x)=x2, 则f(-3)=9.
解法二再取特值得f(0)=0,再令y=-x得,f(x)+f(-x)=2x2,再令y=-x,得f(-3)=9.
解法三右边2xy,有点象完全平方的形式,构造满足条件的特殊函数.
取f(x)=x2满足f(x+y)=f(x)+f(y)+2xy和f(1)=1,则f(-3)=9.
六、 运用知识板块不同的一题多解
例6 过抛物线y2=2px(p>0)的对称轴上一点A(a,0)(a>0)的直线与抛物线相交于M,N两点, 自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.
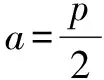
这道题证明垂直的题目,从几何板块知识,向量板块知识,坐标计算知识板块等不同知识板块,有不同的解法.
从几何板块知识入手:
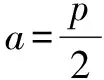
由抛物线的定义得:|MA|=|MM1|,|NA|=|NN1|,
所以∠MAM1=∠MM1A,∠NAN1=∠NN1A.
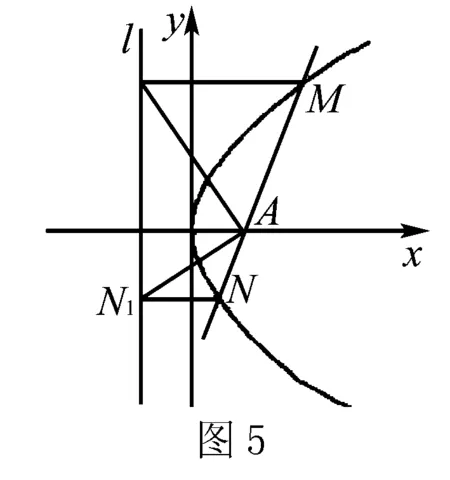
如图5,设准线l与x轴的交点为A1,因为MM1∥NN1∥AA1,
所以∠A1AM1=∠MM1A,∠A1AN1=∠NN1A.
而∠A1AM1+∠MAM1+∠A1AN1+∠NAN1=180°.
即2∠A1AM1+2∠A1AN1=180°.
所以∠A1AM1+∠A1AN1=90°.
故得AM1⊥AN1.
从向量板块知识入手:
证法二设∠MAx=θ,
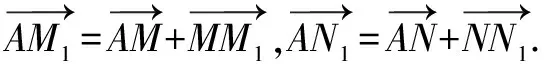
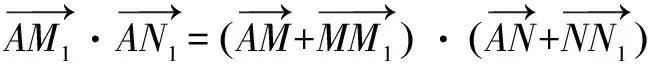
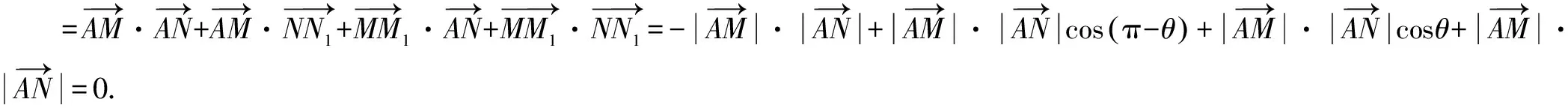
从坐标计算板块知识入手:
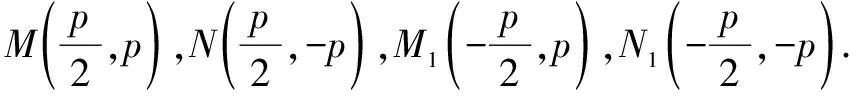
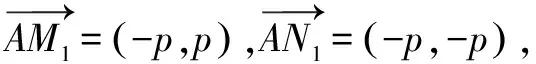
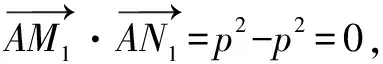
所以AM1⊥AN1.
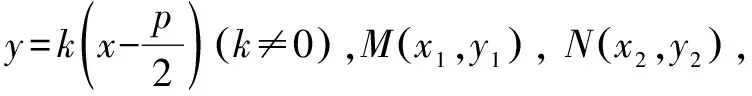
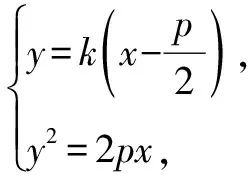
所以AM1⊥AN1.
综合上述(1)、(2),必有AM1⊥AN1.
可见,不同解法反映学生的视角与思路是不同的,本质就是把数学知识图形化,坐标化,代数化,知识点之间融合化,从一道题中学会一类题,甚至构建一个知识系统.达到举一反三,一箭双雕的目标.



