王莲霞
(河南省天一文化传播股份有限公司 450000)
一、静态问题“动态分析”
所谓“动态分析法”就是指将静态的问题放置到一系列的运动变换过程中去加以思考分析.这样处理具体问题,有利于从运动变换的角度对问题进行探究.值得一提的是,必须注意具体地“动”的方式,通过在“动”中去关注、运用题设条件,有助于迅速分析、解决目标问题.灵活运用这种将静态问题动态化的分析思想,往往可以得到简捷、新颖别致的解法.
例1 (1)若方程x2-x-a=0在[-1,1]上有实数解,则实数a的取值范围是;
(2)若方程x2-x-a=0的两个不同实数解都在[-1,1]上,则实数a的取值范围是.
解析由方程x2-x-a=0,得x2-x=a.
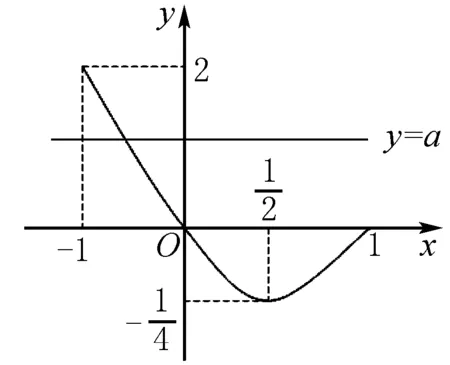
图1
在同一坐标系内分别画出函数y=x2-x(-1≤x≤1)的图象与直线y=a,如图1所示.
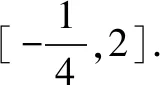
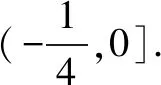
评注一般地,若关于x的方程a=f(x)有实数解,则参数a的取值范围就是函数f(x)的值域;若关于x的方程a=f(x)在某区间上有两个不同的实数解,则应使直线y=a与曲线y=f(x)有两个不同的公共点,进而让动直线y=a上下平移分析即得参数a的取值范围.
二、关注直线与圆有公共点的“非常规”应用
一般地,设d表示圆心到直线的距离,r表示圆的半径,则直线与圆有公共点(即相切或相交),等价于圆心到直线的距离小于或等于圆的半径,即d≤r.灵活运用这一结论,可顺利解决许多貌似与直线和圆无关的数学问题,往往巧妙之极,真的令人拍案叫绝!
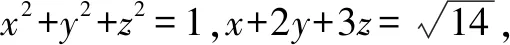
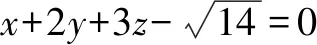
评注本题求解的关键在于先将变量看作常量,灵活构造直线和圆;再根据直线与圆有公共点的充要条件,构建不等式,将“不等”转化为“相等”.
三、关注三角函数的最值与导数的“约会”
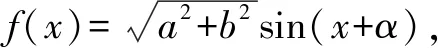
例3 (2013新课标全国卷Ⅰ)设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=____.
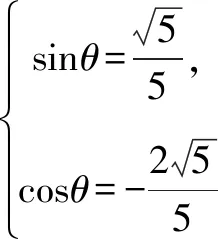
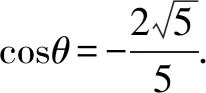
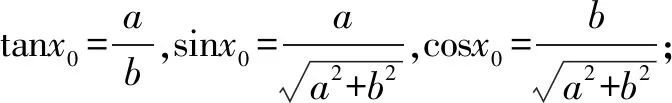
四、利用“解析法”,处理解三角形问题
处理解三角形问题的常规解题思路就是结合题意灵活运用正、余弦定理及面积公式加以求解.但有些解三角形问题如此分析,往往过程较繁很难顺利求解,这时我们不妨灵活运用“解析法”去探求解题思路,往往可优化思维,简化过程.
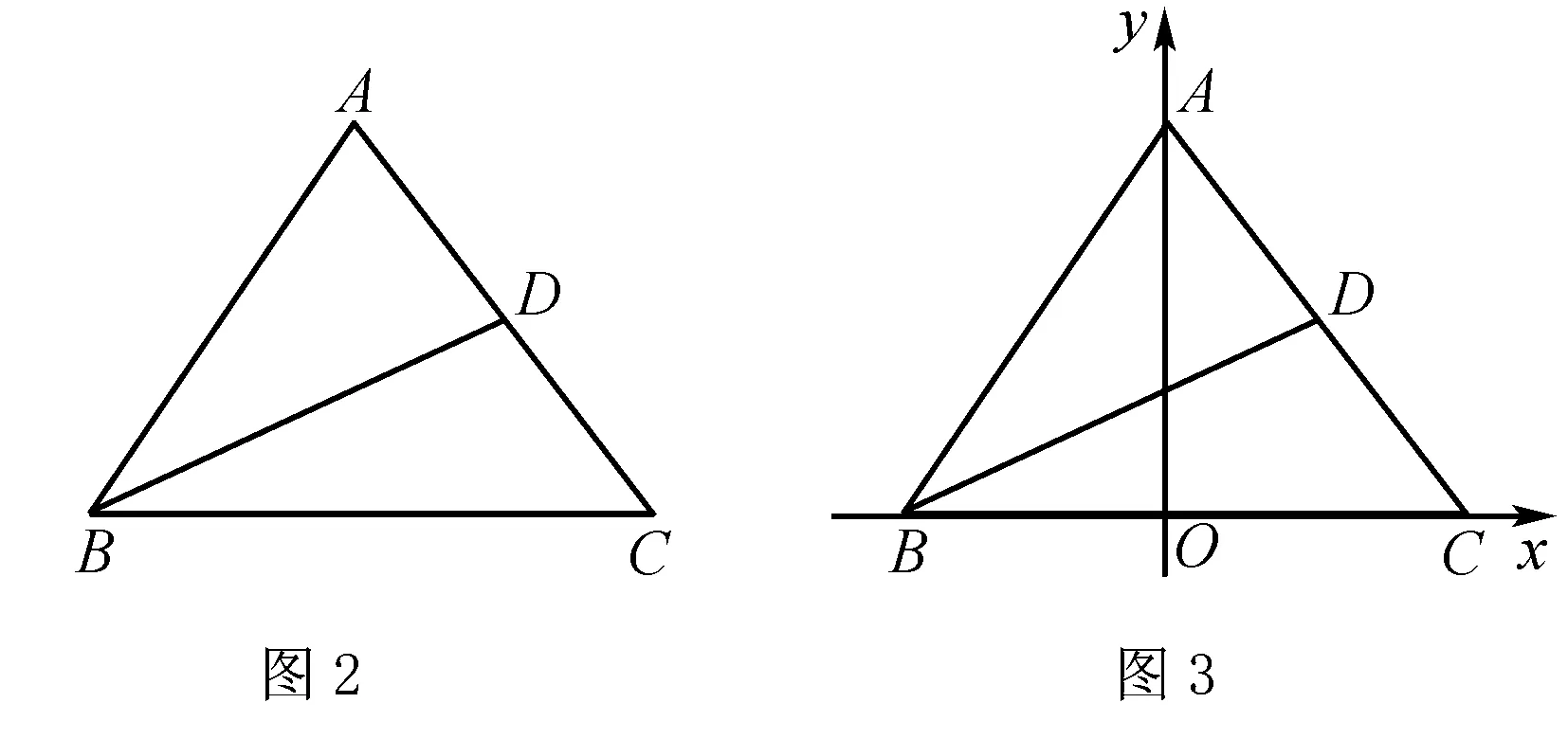
例4 如图2,在等腰三角形ABC中,底边BC=1,底角B的平分线BD交AC于D,求BD的取值范围.
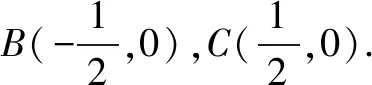
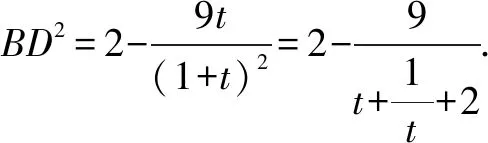
评注上述求解的关键在于准确分析BD2的函数表达式,转化为求函数的值域问题.
综上,不同的思维切入点,往往可获得不同的解题体验,真可谓“横看成岭侧成峰,远近高低各不同”,需要我们在学中“悟”,在“悟”中不断提升解题技能.



