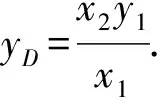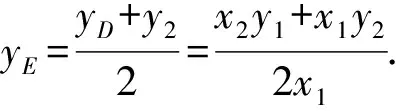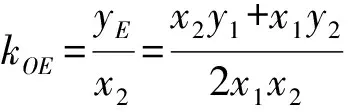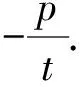高继浩
(四川省名山中学 625100)
1 试题呈现
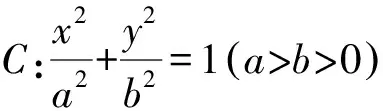
(1)求椭圆C的方程;
(2)设过点P(2,1)的直线l与椭圆C交于不同的两点M,N,过点N作x轴的垂线,与直线BM交于点D,E为线段DN的中点.证明:直线BE的斜率为定值.
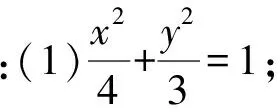
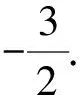
2 问题提出
改变试题第(2)问点P的坐标后,直线BE的斜率还为定值吗?注意到试题中B,P两点的横坐标相同,利用软件GeoGebra作图发现,若保持点P的横坐标不变,改变点P的纵坐标且点P不与点B重合,则当直线l绕着点P转动时,直线BE的斜率仍为定值.这是否具有一般性呢?
3 推广探究
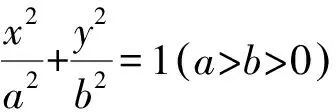
证明显然直线MN的斜率存在,设其方程为y-t=k(x-a),与椭圆方程联立,消去y整理,得
(b2+a2k2)x2+2a2k(t-ak)x+a2(a2k2-2atk+t2-b2)=0.
设M(x1,y1),N(x2,y2),则Δ>0,且
直线BM的方程为
令x=x2,得
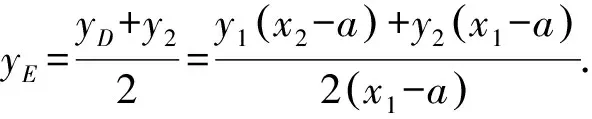
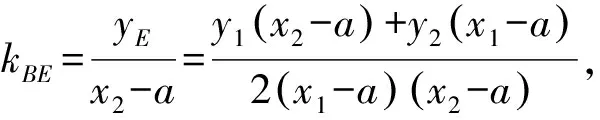
其中分子
y1(x2-a)+y2(x1-a)
=(kx1-ak+t)(x2-a)+(kx2-ak+t)(x1-a)
=2kx1x2+(t-2ak)(x1+x2)+2a(ak-t)
=[2a2k(a2k2-2atk+t2-b2)+(t-2ak)·2a2k·(ak-t)+2a(ak-t)(b2+a2k2)]/(b2+a2k2)
分母
2(x1-a)(x2-a)
=2[x1x2-a(x1+x2)+a2]
=2·[a2(a2k2-2atk+t2-b2)-a·2a2k·(ak-t)+a2(b2+a2k2)]/(b2+a2k2)
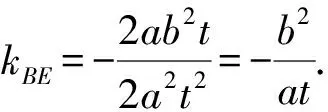
考虑左顶点得到:
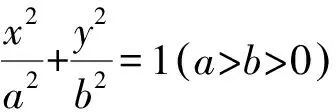
参照命题1可证得.
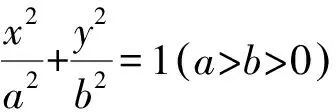
考虑下顶点得到:
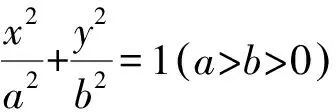
4 类比探究
在双曲线和抛物线中有:
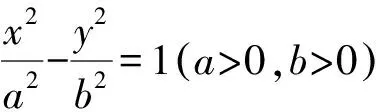
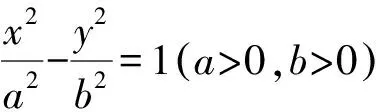
命题5(命题6)的证明过程与命题1类似,略.
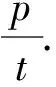
证明显然直线MN的斜率存在且不为零,设其方程为y=kx+t,与抛物线方程联立,消去y,得k2x2+2(tk-p)x+t2=0.
设M(x1,y1),N(x2,y2),则Δ>0,且