袁梅红


[摘 要] 很多源于教材又高于教材的中考数学综合试题都是践行数学核心素养的最佳体现,教师在实际教学中应强化核心知识教学,并引导学生思考、探索问题的解决方法,使学生在不断的探索、反思与感悟中最终实现全面发展.
[关键词] 初中数学;核心素养;抽象;建模;直观想象
教育部早在2014年就提出了以科学性、时代性、民族性为基本原则,培养学生核心素养的具体要求,当今中考试题命题也都体现了源于教材又高于教材的特点,这些灵活多变、旧题新出的中考试题正是践行数学核心素养的最佳体现. 本文结合中考某一试题,谈谈笔者培养学生数学核心素养的实践性思考.
这是一道来源于折纸的数学探究综合题,矩形、相似三角形、勾股定理、二次函数与一元二次方程、直线与圆等诸多知识以及初高中衔接的内容都在此题中得到了巧妙的设计与融合,此题可以通过多种方法求解,但如果解题追求简洁且快速,就需要学生具备丰富的数学核心素养与解题经验,并渗透数形结合、函数、方程、转化、分类讨论等思想方法. 这道试题对学生的思维能力、计算能力都提出了较高的要求,要践行数学核心素养,就需要这样综合性的好题来体现.
数学抽象与建模
学生初读此题往往会有很多疑惑:△OCD沿OD折叠时,点C的对应点C′是否会落在直线l:y=-x+7上?假如落在直线l:y=-x+7上,与哪些量相关,又取决于哪一个相关的量?点C的对应点在直线l:y=-x+7上时是不是只有两个?学生的困扰基本都集中在折叠后点C的对应点C′上,因此,教师教学时可以引导学生回归实践,并探寻问题的本质,继而定位C′.
师:请同学们取出自备矩形白纸一张,并按图5所示的方式折叠矩形的一角,使折痕经过点O. (最终目的:通过提问帮助学生建立数学模型)
师:你在折叠白纸时遇到了哪些问题?
生:没有告诉我们应该沿哪一条折痕折叠.
师:对,但是因为没有这一条件,因此大家折的就会不一样,请大家观察一下大家折的是不是完全不同呢?
生:有一点是相同的,即都会经过点O.
师:很好,大家尝试一下各种不同的折叠方法.
(学生操作并思考)
师:你在过点O折叠矩形一角的过程中有何感悟?能分享一下吗?
生:其实我们是把线段OC绕点O旋转.
师:很好,过点O任意折叠矩形的一角时,点C肯定会落在哪里?
生:肯定会落在以点O为圆心、OC长为半径的圆上,如图6.
师:很好,请大家观察图形并思考老师为大家设计的问题:
(1)过点O折叠矩形的一角时,点C是否一定会落在直线l:y=-x+7上?
(2)过点O折叠矩形一角时,点C的对应点C′和直线l:y=-x+7之间存在怎样的位置关系?
(3)折叠后点C的对应点C′和直线l:y=-x+7的位置关系由什幺因素决定?跟哪些量有一定的关系?
从上述一系列问题的讨论中学生很快发现,点C和直线l:y=-x+7的位置关系实际上就是直线和圆O的位置关系,圆心到直线l:y=-x+7的距离d和r(OC)的大小关系又决定了直线和圆的位置关系,因此直线与圆的位置关系的数学模型成了解决此题的关键. 由题意可得d=<5,因此,直线和圆必然存在两个交点. 令交点为E,F,如图7,定点E,F找到了,因此AE,AF就必然为定值.
经过上述分析,一系列探究问题被化归成了定点E,F到矩形OABC的顶点、边界、静态线段的距离都是定值这一问题. 因此,问题很快转化成了图8所示的以下问题:在矩形OABC中,经过点O的某一直线折一个“拐”并使点C落在边MN上,同理,点F的问题一样可以转化.
在图8中找出与矩形OABC相关的线段或已知线段,并去掉多余图形,继而对其提炼,可以得到图9所示问题:在矩形OMNC中,沿直线OD折叠,点D恰好与直线MN上的点E重合,已知EN=1,求CD的长. DE的长又该如何求解呢?学生头脑中熟悉的翻折模型此时被图形操作与问题转化很快唤醒:折叠图形后使其一个角的顶点落在某条边所在直线上,即将矩形一个角的顶点通过折叠,落到相邻的边MN上,问题回到了学生所熟悉的模型上,勾股定理的模型即可用于此题的求解,几何问题也因此转化成了代数问题.
直观想象与建模
问题(4)除了标准答案中的解决方法外,还可以通过数学建模、直观想象来解决,且整个计算过程更加简便:要让△EFP为直角三角形,可以将问题分成三种类型进行分类讨论.
1. 将点E作为直角顶点
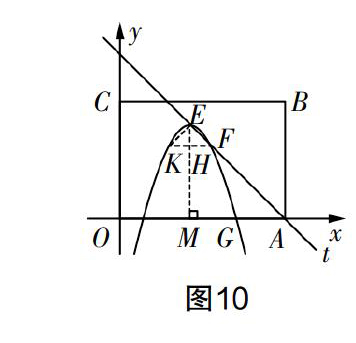
如图10,作FH⊥EM于点H,延长FH与抛物线相交于点K,连接EK,根据已知条件和图形直观想象,可以看出△FHE是等腰直角三角形,∠FEH=45°. 根据抛物线的对称性,观察图形可知∠KEH=∠FEH=45°,因此∠FEK=90°,由此可知点K满足条件,即当点P与点K重合时,此时的点P满足条件. 因为此时的点P和点F关于抛物线的对称轴对称,由F(4,3)得满足条件的点P的坐标为(2,3).
2. 将点F作为直角顶点
过点F作EF的垂线,与抛物线相交于点P,观察图形可得P(1,0). 此时通过联想勾股定理进行验证:可求得FP2=18,EF2=2,EP2=20,显然FP2+EF2=EP2,由勾股定理的逆定理可知△PEF是直角三角形,继而知点P(1,0)满足条件.
3. 将点P作为直角顶点
解法与标准答案相同.
这一数学难题通过直观想象、数学猜想、数学推理等方法就这样神奇而简洁地得到了解决,数学的内在美也在这样分类讨论的过程中得到了很好的体现.
践行数学核心素养
本文所分析的这一试题构思与数据设计得都很巧妙,题中只有5和7两个简单的数据,直线方程是y=-x+7(即x+y=7);第(1)小问可求得E(3,4),F(4,3),题中数据因此多了3和4. 经过数据分析与数学运算可得3+4=7(x+y=7),32+42=52(x2+y2=52). 根据图形的观察进行直观想象和逻辑推理可知x,y对应3,4,因此x=3,y=4或者x=4,y=3. 因此,E(3,4),F(4,3)不仅在直线y=-x+7上,而且这两点还在以原点为圆心、5为半径的圆(x2+y2=52)上. 再结合解题所得的答案有数据:1,2,3,4,5,7,虽然只有简单的6个数字,但数学的内在美和魅力都在这一过程中惊奇地展现了.
翻折的实践操作活动将全等变换、相似构造很好地融进了矩形问题中,因此,此题的教学重在引导学生对问题和数据进行分析,并构造出基本图形. 因此,读懂图形与题意并对隐含条件进行深入挖掘,是解题过程中首先要做的,解题者必须具备扎实的基础知识才能更好地解题. 启发、引导学生对问题进行探究、猜想、思考、反思、感悟是此题解题教学的精髓所在,也是培养学生能力与品质的重要途径. 因此,教师在实际教学中应首先强化核心知识教学,并引导学生思考、探索问题的解决方法,使学生在不断的探索、反思与感悟中最终实现全面发展.



