鲁永明


[摘 要] 本文通过用垂直理念证明勾股定理和解决典型例题来阐述垂直在几何解题中的价值. 若能提炼出问题中的垂直,往往能使问题回归源头,易于解决. 同时,其也说明了构建理念的重要性.
[关键词] 垂直;纵横理念;勾股定理
问题由来
笔者有幸拜读了重庆市万州高级中学张进老师发表在《中学数学教学参考》2017年1-2期上的一篇文章——《探索一道竞赛试题解法的心路历程》,这是第24届“希望杯”中的一道填空题,题干如下:
如图1,在梯形ABED中,∠D=∠E=90°,△ABC是等边三角形,且点C在DE上,如果AD=7,BE=11,则△ABC的面积为______.
张老师居然探索出13种解法,简直匪夷所思,令人叹为观止!相信对于有一定基础的学生一定会脑洞大开、受益匪浅!
纵横理念
那幺,是否还有其他解决途径呢?笔者想到了垂直(称为纵横). 笔者在长期的教学实践中感悟到了垂直关系在解决几何问题中的重要地位,于是笔者在几何学中渐渐有了一个重要的理念——纵横理念,即在解决几何问题的过程中,尽可能提炼出问题中的垂直关系,并以垂直为线索展开实践、探索活动,直至问题解决.
人类进化的标志性特征是直立行走,从数学的视角来看,直立行走就是垂直,而垂直只是一种表象,背后蕴藏着一股强大的生命能量!勾股定理就是最好的例证之一!把直角看作纵横,勾股定理就是揭示斜与纵横之间的一种数量关系.
纵横理念证明勾股定理
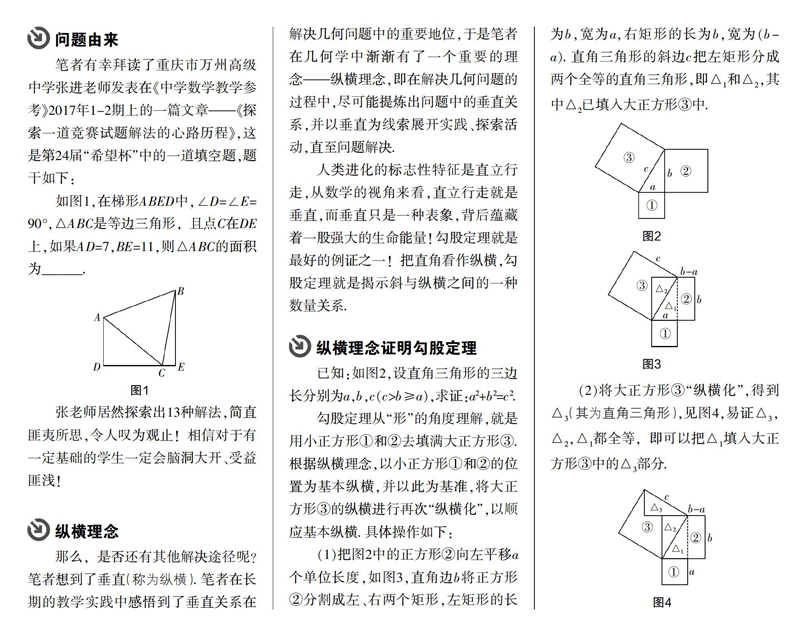
已知:如图2,设直角三角形的三边长分别为a,b,c(c>b≥a),求证:a2+b2=c2.
勾股定理从“形”的角度理解,就是用小正方形①和②去填满大正方形③. 根据纵横理念,以小正方形①和②的位置为基本纵横,并以此为基准,将大正方形③的纵横进行再次“纵横化”,以顺应基本纵横. 具体操作如下:
(1)把图2中的正方形②向左平移a个单位长度,如图3,直角边b将正方形②分割成左、右两个矩形,左矩形的长为b,宽为a,右矩形的长为b,宽为(b-a). 直角三角形的斜边c把左矩形分成两个全等的直角三角形,即△和
回到本文开头的那道竞赛题,依然可用纵横理念来演绎不同的解法.
分析 从图1中可以提炼出两个纵横:“U”字形纵横,即AD⊥DE,BE⊥DE构成了本题的基本纵横;而等边三角形的特殊性在于,它是由两个全等的含30°角的直角三角形构成的,所以,很容易想到高——垂直,这就是等边三角形ABC的纵横. 类似勾股定理的证明方法,对这个三角形再次进行“纵横化”,以顺应本题的基础纵横,使两个纵横互通有无.
回顾反思
“不忘初心,方得始终. ”纵横是不是数学世界里的源头?是不是数学世界里的初心?这也许是个大课题,但人类探索“源头”的步伐从未停止. 《周髀算经》中记载了“周公问算”,即商高曰“数之法出于圆方,圆出于方,方出于矩”;《几何原本》从五个公设出发,建立了一个完整的欧氏几何体系;笛卡儿在垂直的基础上创建了直角坐标系……
“理念是行动的先导. ”让解题成为孩子建立理念和践行理念的平台,成为孩子们渐修的一种途径,并在这个过程中不断发展和完善自己的理念体系,提升认识事物的境界.
探究新知需要实践、操作、猜想、证明,建立理念的过程同样需要一个曲折的积累过程,积累到一定的量时,这些理念便会慢慢清晰,成为孩子人生中的公设. 他们可以从这些理念公设出发,书写自己生命中的《几何原本》.



