董浩,孙成飞,周震昊,王雨龙,丁应章
(中建三局集团有限公司,湖北 武汉 430000)
随着人们对美好生活的不断追求,出现了各色各异的建筑结构,我国现行《混凝土结构设计规范》(GB50010-2010),经过多次改进其理论更为科学合理,更趋于国际化。但在应对形形色色的建筑结构时,为使结果更好地与实际相符,规范中的某些计算公式会较为麻烦。例如计算对称配筋矩形截面小偏心受压构件时,求解相对受压区高度ζ需解的三次方程,用于设计很不方便,故“规范”给出了求ζ的近似公式,但按此式计算在准确度上有待商榷。因此,可以使用“牛顿法[4]”对高次方程进行求解,由于需要应用到工程计算之中求解过程不能繁琐,且要求能够快速收敛,以及运用一种改进牛顿法的方法:“牛顿—秦九韶法”[1]。根据数值分析[4]牛顿法与牛顿—秦九韶法的求解,需要对初值有准确的估计,在这种情况下本文列举了另一种解法“黄金分割法”[7],利用黄金分割法收敛快且不需要定义初值的优势,可以更快速地求解高次方程。
1 基于“规范”的近似计算
下面作者简述“规范”中采用简化公式的过程,以便分析其不足。对于对称配筋的小偏心受压柱,根据基本公式和对称配筋的特点,可以导出以下公式:

式(1)为ζ的三次方程,求解很麻烦,故“规范”基于以下理由做出了简化:

由式(2)知y也是ζ的三次函数。但因为在小偏心受压范围内,y与ζ的关系是趋近于线性关系。小偏心受压构件ζ常见范围为:ζb<ζ< 1.6-ζb其中ζb为相对界限受压区高度,对于常用的Ⅰ、Ⅱ和Ⅲ级钢筋,ζb值分别为0.614、0.544及0.528,则 ζ(1-0.5ζ)的值在 0.39~0.50之间,故“规范”取ζ(1-0.5ζ)=0.43,将其代入式(1)即得求ζ的近似公式:

则配筋公式:

可以总结两点。
①在计算矩形截面对称配筋小偏心受压构件时关键是需求解ζ。
②用上述规范所诉的近似算法进行设计时,产生误差的原因在于:在小偏心受压范围内,虽然ζ的三次式(2)趋近于直线,但对不同材料其直线回归方程是不一样。若不分情况,一律将 ζ(1-0.5ζ)的结果取为常数0.43,即把采用不同材料时的直线回归方程全都视为y=0.43(ζb-ζ)/(ζb-0.8),显然与实际不完全相符,导致一定误差[3]。
2 各类数值解法
2.1 牛顿法
牛顿法也称牛顿—拉佛森法,是迭代法的一种,其收敛速度通常比一般的迭代法都快,下面简述一下牛顿法的原理[4]:
牛顿法是用泰勒公式展开的一种迭代方法,设方程f(x)==0的根x*的近似值为将函数f(x)在点xk展开:

舍去高阶项上式可近似表达:

整理上式可得到迭代式:

根据以上迭代式选取初值x然后反复迭代就可以得到满足精度的x值,利用此原理可以求解公式(1)的三次方程,根据上述迭代式可知求解f(x)的函数值与一阶导数值即可,因此,可以发现由公式(1)得到的三次方程组多项式需要求解平方乘法然后再加法,在计算步骤中虽然较解三次方程组简单一点,但计算量太大,不适合手算。基于此,李汝庚[1]提出了改进后的牛顿—秦九韶法。
2.2 牛顿—秦九韶法
上一节的“牛顿法”,虽然思路清晰,方法易懂,但有函数值及一阶导数的求解,计算量大了。早在我国古代就有秦九韶法来解决有关于多项式f(x)在任意x的泰勒展开式前面系数的问题。牛顿—秦九韶法[5]由我国古代的秦九韶法与西方近代的牛顿迭代法相结合,本方法适用于解决建筑结构中的高次方程。例如本文所述的矩形截面对称配筋小偏心受压构件的计算求解,相对受压区高度ζ的三次方程问题,若用牛顿—秦九韶法求解则颇简便。下面以一个三次多项式为例,说明该法的数学原理及算法步骤。

关于f(x)在任意点x0处的泰勒展开式:

按如下格式计算:

格式中第一行是式8的各项系数,然后以下各行数均按式10计算:

例如第二行的计算如下:(因为b0左边没有数字所以b0=a0

由此可得按式(9)表示的f(x)在x0处的泰勒展开式:
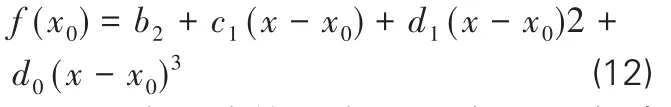
上述方法就是秦九韶法[7],此法利用乘法和加法代替求导计算,大大简化了计算过程,对于求任意高次多项式在任意点x0处的展开式系数非常简便适用。而牛顿法的迭代公式(7)首先需求解一阶导数和函数值,再应用迭代公式反复迭代才能得到数值解,对比而言计算量过大。
2.3 黄金分割法
根据以上分析,无论是迭代法还是改进后的迭代法,对于方程的求解都依赖于初值的选取,对于对称配筋小偏心受压构件ζ的常遇范围为ζb<ζ<1.6-ζb,因此,ζ比较好的初始值ζb便可在此范围内拟定,可取ζb与(1.6-ζb)的平均值,近似为0.8左右[5]。但建筑结构中高次方程多样,并不都像对称配筋小偏心受压构件中的ζ可以选取出初值。例如分析高层建筑的固有振动时,设自振频率为ω,特征值λ=1/ω2,经推导可得高层建筑确定频率的高次方程为另外,当高次方程中存在多解时,上述迭代法会出现收敛速度慢的缺点。
黄金分割法[6]求高次方程的数值解,能克服上述两大缺点。黄金分割法的算法思想为对于连续函数F(x),在闭区间[a,b]内有且仅有一个实数根x,令x1=a,x2=b。若F(x1)=0或F(x2)=0,则x=x1或x=x2即为所求实数根;否则求取新的区间利用①=a+(b-a)×0.618(设a<b)求取第一个点;再利用②=(a+b)-①=(大+小)-中求取第二个点,比较F(①)与F(②)的大小,得到新的区间在新区间内重复以上过程,直到所求有根区间在精度范围内为止,即可得到实数根x[6]。
用黄金分割律求高次方程的数值解主要用到下面两个公式:
①=a+(b-a)×0.618(设a<b)
②=(a+b)-①=(大+小)-中
由于黄金分割法需要提前知道根的区间,可以利用以下两种方式确定:a.利用连续函数根的存在性定理(二分法确定根所在的区间)2)根据建筑结构的理论大致确定根的区间如小偏心受压构件ζ,可以明确知道它的根在[0,1]区间。
3 算例
例1已知:轴向力设计值N=3500kN,弯矩M1=0.88M2,M2=360kN·M,截面尺寸b=400mm,h=700mm,混 凝 土 强 度 等 级 为C40,钢筋用HRB400钢筋,构件计算长度Ic=I0=3.3m,对称配筋[3]。
经判断为小偏心受压,使用规范近似公式计算得ζ=0.6826:由(1)式化简得到以下高次多项式:

用解三次方程的方法算得的精确解为ζ=0.6975。
3.1 使用牛顿—秦九韶法求解

3.2 使用黄金分割法计算
a.F(0)=-0.841<0;F(1)=0.1163>0
则ζ的解在[0,1]之间;
第一个点:
①=0+(1-0)×0.618=0.618
第二个点:
②=(1+0)-0.618=0.382
比较F(0.618)与F(0.382)大小

b.得到区间[0.618,1]
第一个点:①=0.618+(1-0.618)×0.618=0.854076
第 二 个 点 :② =(1+0.618)-0.854076=0.763924
比较F(0.763924)与F(0.854076)大小

c.得到区间[0.618,0.763924]
第一个点:①=0.618+(0.763924-0.618)×0.618=0.708181
第 二 个 点 :② =(0.763924+0.618)-0.708181=0.673743
比较F(0.673743)与F(0.708181)大小

d.得到区间[0.673743,0.708181]
第 一 个 点 :① =0.673743+(0.708181-0.673743)×0.618=0.9650
第 二 个 点 :② =(0.708181+0.673743)-0.6950=0.686924
e.F(0.6950)=-0.001221075;
F(0.686924)=-0.0046769
此时可以看到F(0.6950)已经很接近0,说明0.6950接近真实解;
利用精确度是1%此时F(0.6950)=-0.001221075精确度0.1%可以停止迭代。
f.取ζ=0.6950,精确值为0.6975
4 结语
对实际的建筑结构,其数学模型难以用数学分析得出解析解,须按数值计算方法寻求近似解,迭代法是数值计算中最常用的方法。本文仅介绍了建筑结构中对称配筋矩形截面小偏心受压构件有效又有特色的数值解法。此法同样可用于求解建筑结构中其他有关高次方程的问题。通过对比三种计算方法及分析算例可以得到以下结论。
①利用改进的牛顿法与黄金分割法对小偏心构件相对受压区高度的计算,可以得到简化公式更加精确的解。
②对于小偏心构件的计算,改进的牛顿迭代法虽然求解速度较快且较精确,但是其对于第一次迭代的初值要求严苛,然而不是所有建筑结构中的高次方程都有比较准确的估值。因此,相比之下黄金分割法更适合应用于特殊情况。
③黄金分割法更适用于计算机编程,通过计算机并行计算,可以对已有进行算法优化。



