雷亚庆
(江苏省南京市大厂高级中学 210044)
含根式函数的最值问题具有灵活性强、难度大的特点,很多同学望而生畏,往往不知道从哪入手,尤其是双根式函数更是难点.实际上根式函数没有想象的那幺可怕,只要我们认真分析题意,注意条件的应用,养成正确的解题习惯,即可找到合理恰当的解法,使此类问题顺利加以解决,下分类举例说明.
一、利用函数单调性
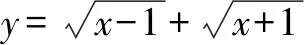
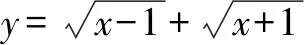
由于函数y=x-1和y=x+1在[1,+)为增函数,所以在[1,+)上单调递增.
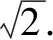
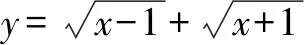
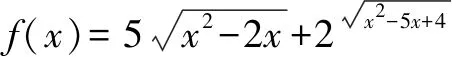
解定义域为(-,0]∪[4,+),显然函数在(-,0]上单调递减,在[4,+)上单调递增.因此f(x)min=min{f(0),f(4)}=f(0)=4.
二、利用换元去根号
1.换元消去根号
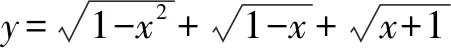
解求得定义域为:{x|-1≤x≤1}.

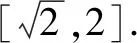
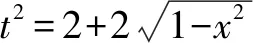
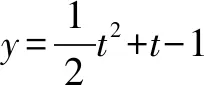
2.三角换元化掉根号
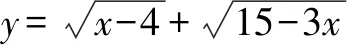
分析求根式函数的值域是一个难点,特别是双根式函数,实际上如果我们养成解决函数问题先明确定义域的好习惯的话,就会发现隐藏的解题信息,利用三角代换,就可以把根式函数转换为三角函数问题处理.
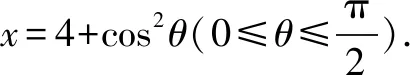
∴函数的值域为[1,2].
三、利用平方去根号
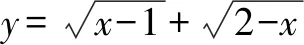
解析求得定义域为[1,2].
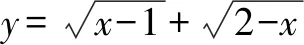
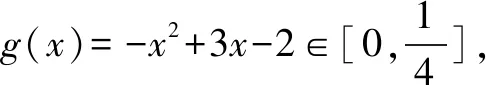
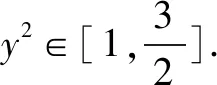
四、利用几何意义
1.构造距离
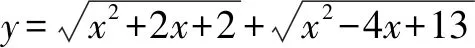
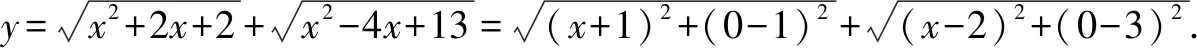
设点P(x,0),A(-1,1),B(2,3),
问题转化为:在x轴上找一点P,使PA+PB最小作点A关于x轴对称的点A′(-1,-1),显然当点P为直线A′B与x轴交点时PA+PB有最小值即A′B=5.
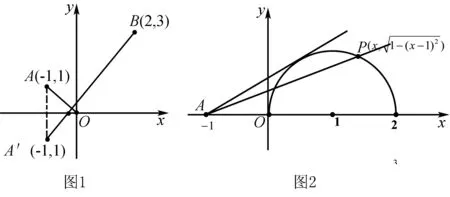
2.构造斜率
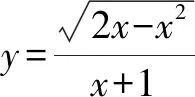
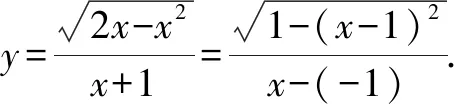
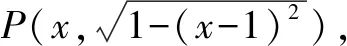
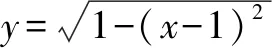
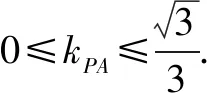
五、利用向量数量积的性质
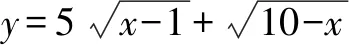

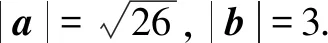
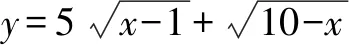
六、利用分子有理化
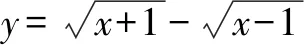
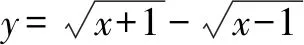
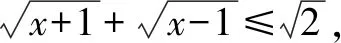
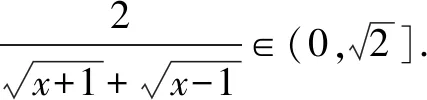
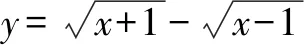
七、构造对偶式求解
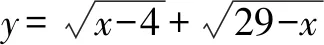
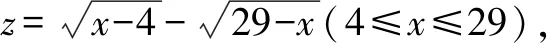
则y2+z2=50,即y2=50-z2.
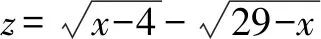
所以当4≤x≤29时,z∈[-5,5],
所以y2=50-z2∈[25,50].
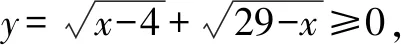
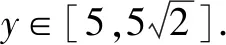
总之,解决根式函数的最值问题时,我们要养成良好的审题和解题习惯.如审题要注意挖掘目标函数的结构和隐含信息,解函数题时一定养成先求定义域的好习惯,只要这样我们就可以通过换元,构造,把问题转化为我们熟悉的函数最值模型,从而使问题得以解决.



