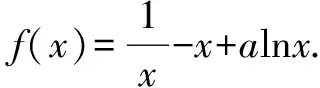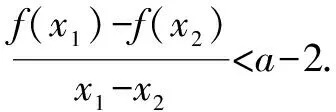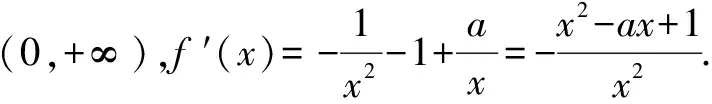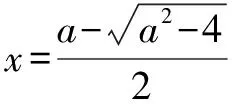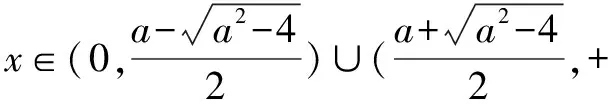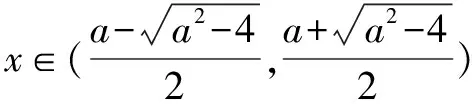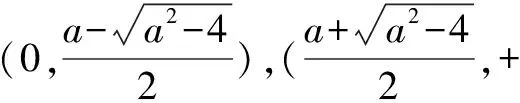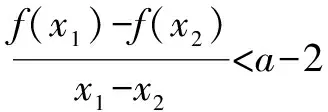张 庆
(江苏省徐州市侯集高级中学 221300)
按导函数零点能否求精确解可以分为两类:一类是数值上能精确求解的,称之为“显零点”;另一类是能够判断其存在但无法直接表示的,称之为“隐零点”.对于隐零点问题,由于涉及灵活的代数变形、整体代换、构造函数、不等式应用等技巧,对学生综合能力的要求较高,成为考查的难点.
一、分离函数法
例1 已知函数f(x)=ax+xlnx(a∈R).
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x-1) 解析(1)∵函数f(x)在区间[e,+∞)上为增函数, ∴f′(x)=a+lnx+1≥0在区间[e,+∞)上恒成立, ∴a≥(-lnx-1)max=-2. ∴a≥-2. ∴a的取值范围是[-2,+∞). (2)当a=1时,f(x)=x+xlnx,k∈Z时,不等式k(x-1) 令h(x)=x-lnx-2(x>1). ∴h(x)在(1,+∞)上单调递增, ∵h(3)=1-ln3<0,h(4)=2-2ln2>0, 存在x0∈(3,4),使h(x0)=0, 即当1 当x>x0时,h(x)>0,即g′(x)>0, g(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增. 令h(x0)=x0-lnx0-2=0,即lnx0=x0-2, k ∴kmax=3. 点评变量分离是数学中最常见的一类求解方法,本例中除了采用分离变量的方法外,还需要通过函数构造进行求解,这类求解方法的好处在于不需要对问题进行分类讨论,从而使得对问题的求解更加的简便. 例2 设函数f(x)=e2x-alnx. (1)讨论f(x)的导函数f′(x)的零点的个数; 当a>0时,方程g(x)=a有一个根,即f′(x)存在唯一零点; 当a≤0时,方程g(x)=a没有根,即f′(x)没有零点. (2)证明由(1)可设f′(x)在(0,+∞)上的唯一零点为x0,当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0. 故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,所以[f(x)]min=f(x0). (1)讨论f(x)的单调性; ①若f′(x)≤0,当且仅当a=2,x=1时f′(x)=0,所以f(x)在(0,+∞)上单调递减. (2)证明由(1)知,f(x)存在两个极值点时,当且仅当a>2. 由于f(x)的两个极值点x1,x2满足x2-ax+1=0, 所以不妨设x1 又g(1)=0,从而当x∈(1,+∞)时,g(x)<0. 点评利用导数解决函数问题常与函数单调性的判断有关,而函数的单调性与其导函数的零点有着紧密的联系,设而不求的方法一般在圆锥曲线中经常遇到,其实在函数问题中,若遇到函数极值,零点问题时该方法也是处理该问题的一种常见处理方式.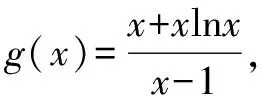

二、整体代换法
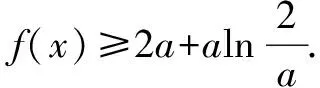
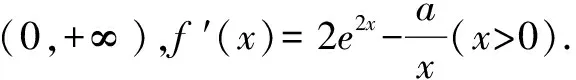
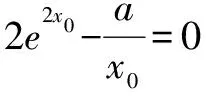
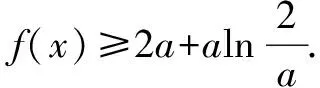
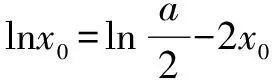
三、设而不求法