陈贤兵
(福建省南平市光泽县第一中学 354100)
运用构造法解题是建立在对问题本质深入理解,准确把握的基础之上,对学生的能力要求较高.授课中应做好相关理论的系统讲解,并做好构造法在解题中的应用示范,使学生掌握运用构造法解题的题型以及相关的应用技巧,提高其解题水平以及解题自信.
1 巧用构造函数,解答数学题
构造函数是解答数学习题的重要构造方法之一.根据题干创设的情境可灵活构造二次函数、三角函数以及一些特殊函数.其中构造函数后还应注重联系所学的函数性质进行解题,针对一些特殊函数还应运用导数知识研究函数的性质,把握函数的增减规律,以达到顺利破题的目的.
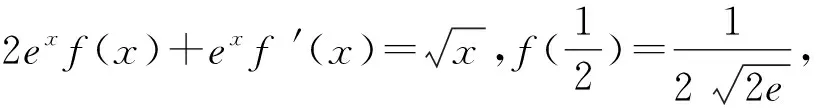
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值,又有极小值
D.无极大值,也无极小值
分析习题仅给出关于函数f(x)的两个等式关系,并不知道函数的具体表达式,难度较大.解题应从给出的两个等式关系入手,联系导数知识,构造相关函数.在把握函数性质的基础上判断函数f(x)是否有极值.
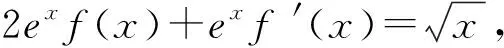

构造函数F(x)=e2xf(x),
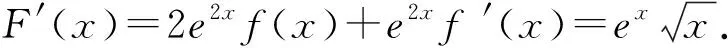
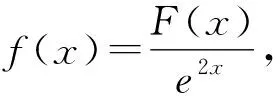
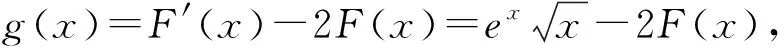
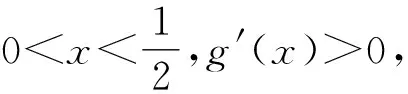
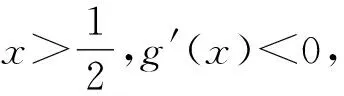
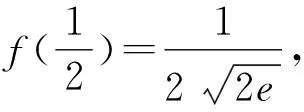
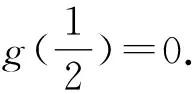
所以f′(x)≤0,函数f(x)在(0,+∞)上单调递减,即当x>0时,其既无极大值也无极小值,故选D.
2 巧用构造数列,解答数学题
高中数学学习的数列类型有等差数列、等比数列,因此,构造数列时应注重对给出的已知条件进行整理、变形,转化成等差或等比数列的形式,然后结合数列的性质、数列前n项和Sn与an之间的关系求出数列的通项公式.结合具体问题灵活运用错位相减法、裂项相消法等技巧进行解题.
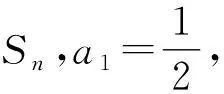
分析因为bn和数列的通项公式an相关,因此,需要先根据已知条件通过构造数列求解出an,而后再代入证明即可.
解析因为an+2Sn-1·Sn=0(n≥2),
an=Sn-Sn-1(n≥2),
代入整理,得
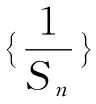
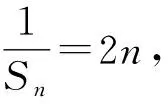
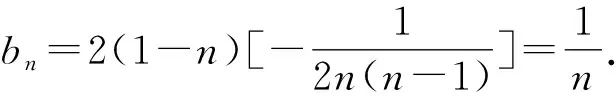
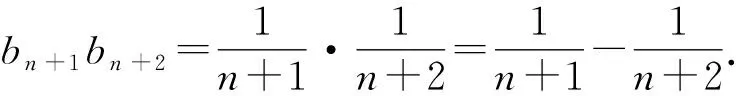
所以
b2b3+b3b4+b4b5+…+bn+1bn+2
3 巧用构造方程,解答数学题
解答高中数学部分习题可对已知条件进行转化,通过构造方程的方式解决.构造方程时应注意充分利用已知条件进行转化,减少参数个数,更好地揭示相关参数之间的内在联系,必要情况下运用函数与方程思想化抽象为直观,借助函数图象理清参数之间的关系,达到顺利解题的目标.
例3 已知实数a,b,c满足a+b+c=2,a2+b2+c2=4,且a>b>c,则a的取值范围为____.
分析习题给出两个等式,看似无从下手,事实上,解题时注重通过等价代换构造相关方程,借助方程知识便可顺利地解答.
解析因为a+b+c=2,所以b+c=2-a.
又因为a>b,a>c,所以2a>b+c.
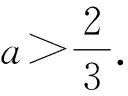
因为b2+c2=(b+c)2-2bc=4-a2,
所以(2-a)2-2bc=4-a2.
整理,得bc=a2-2a,
所以bc是方程x2-(2-a)x+a2-2a=0的两根.
当x=a时,对应函数的值大于零,
即a2-(2-a)a+a2-2a>0.
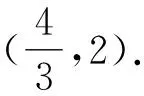
4 巧用构造图形,解答数学题
解答数学习题时构造图形可很好地提高解题效率.构造图形时应积极联系相关知识,吃透已知条件含义,从几何角度分析参数之间的关系,尤其在解决向量问题时构造图形可大大简化解题过程.为使学生掌握运用构造法解答数学问题的技巧,在解题中少走弯路,应启发学生在学习的过程中养成多思考、多总结的良好习惯,并进行多角度分析问题,真正把握相关知识本质.

分析该题采用常规解法难度较大,如能充分吃透向量的几何意义,通过构造图形,便可很快得出正确答案.
解析根据题意建立平面直角坐标系,
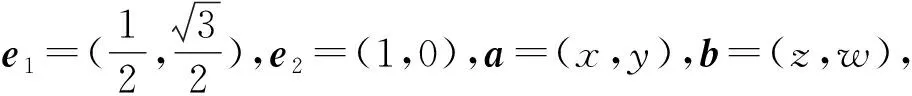
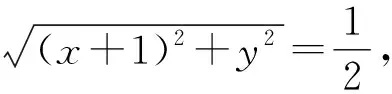
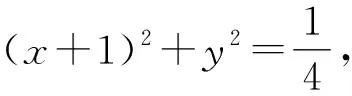
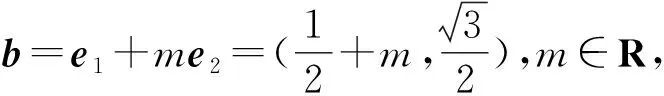
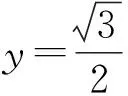
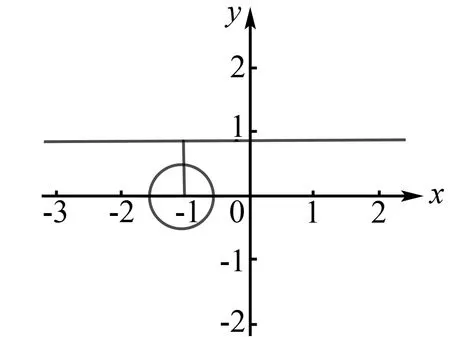
图1
高中数学解题教学中应注重与学生一起总结常用的构造方法,把握不同构造方法之间的区别以及适用题型,通过在课堂上不断强调构造法的重要性,提高学生对构造法重要性的认识,并优选精讲典型例题,为学生展示具体的构造过程.同时,鼓励学生学会听课,做好听课的总结,不断反思,及时找到自身运用构造法解题的不足,加以针对性的夯实.



