廖永福
(福建省厦门第二中学 361009)
题目(2013年北京卷理14)如图1,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为____.
解法1(定义法) 点P到直线CC1的距离的最小值就是异面直线D1E与CC1间的距离.
如图2,过点E作EE1∥CC1交B1C1于点E1,连接D1E1,过点C1作C1F⊥D1E1,垂足为点F,过点F作FP0∥E1E交D1E于点P0,则B1E1=E1C1,P0F∥CC1.
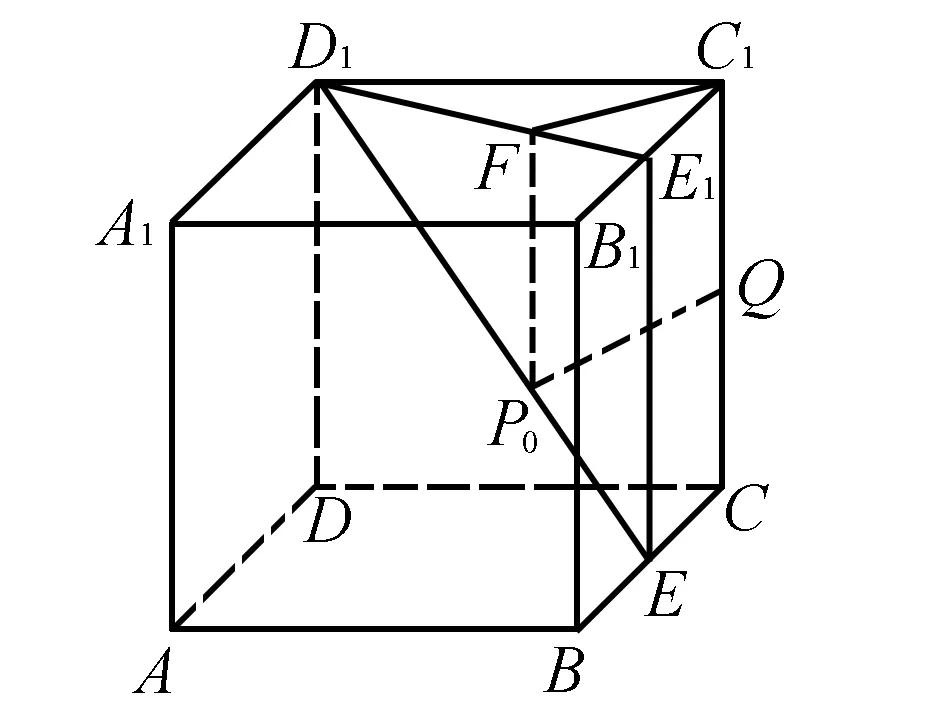
图2
在C1C上取点Q,使得C1Q=FP0.
连接P0Q,则四边形P0QC1F为平行四边形.
因为CC1⊥平面A1B1C1D1,C1F⊂平面A1B1C1D1,所以CC1⊥C1F,四边形P0QC1F为矩形.
所以P0Q⊥CC1,P0Q⊥PF.
因为P0Q∥FC1,所以P0Q⊥D1E1.
又D1E1∩P0F=F,D1E1,P0F⊂平面D1EE1,
所以P0Q⊥平面D1EE1.
所以P0Q⊥D1E.
即P0Q为异面直线D1E和CC1的公垂线.
在Rt△C1D1E1中,由
C1F·D1E1=C1D1·C1E1,得
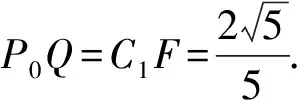
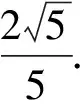
解法2 (等体积法)点P到直线CC1的距离的最小值就是异面直线D1E与CC1间的距离.
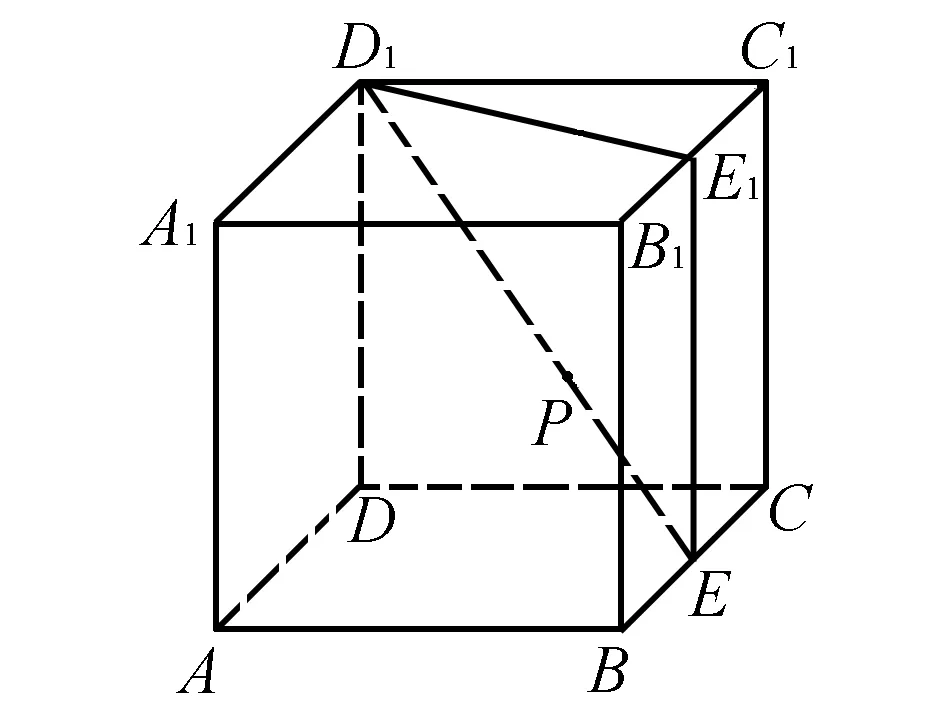
图3
如图3,过点E作EE1∥CC1交B1C1于点E1,连接D1E1,则B1E1=E1C1.
因为EE1⊂平面D1EE1,CC1⊄平面D1EE1,
所以CC1∥平面D1EE1.
所以异面直线D1E与CC1间的距离就是直线CC1到平面D1EE1的距离,就是点C1到平面D1EE1的距离.
设点C1到平面D1EE1的距离为d,
因为VC1-D1EE1=VE-C1D1E1,
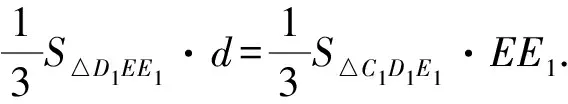
因为CC1⊥平面A1B1C1D1,
所以EE1⊥平面A1B1C1D1.
又D1E1⊂平面A1B1C1D1,所以EE1⊥D1E1.
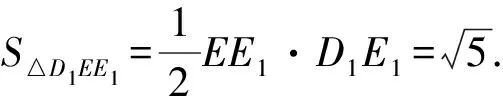
又S△C1D1E1=1,EE1=2,
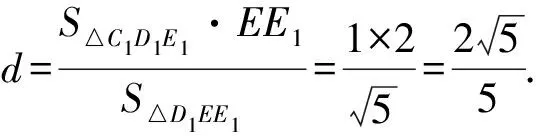
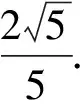
解法3 (等面积法)如图4,过点E作EE1∥CC1交B1C1于点E1,连接D1E1,过点P作PF∥EE1交D1E1于点F,连接C1F,则B1E1=E1C1,PF∥CC1.
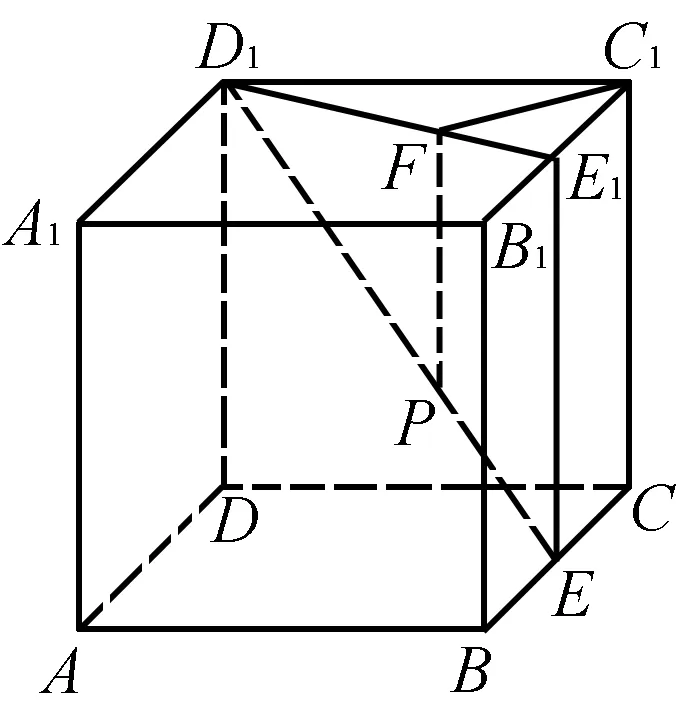
图4
因为CC1⊥平面A1B1C1D1,C1F⊂平面A1B1C1D1,所以CC1⊥C1F.
所以C1F的长就是点P到CC1的距离.
因为点P在线段D1E上运动,所以点F在线段D1E1上运动,当C1F⊥D1E1时,C1F取得最小值.
在Rt△C1D1E1中,由
C1F·D1E1=C1D1·C1E1,得
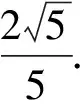
解法4 (向量法)以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图5所示的空间直角坐标系,则C(0,2,0),C1(0,2,2),D1(0,0,2),E(1,2,0).
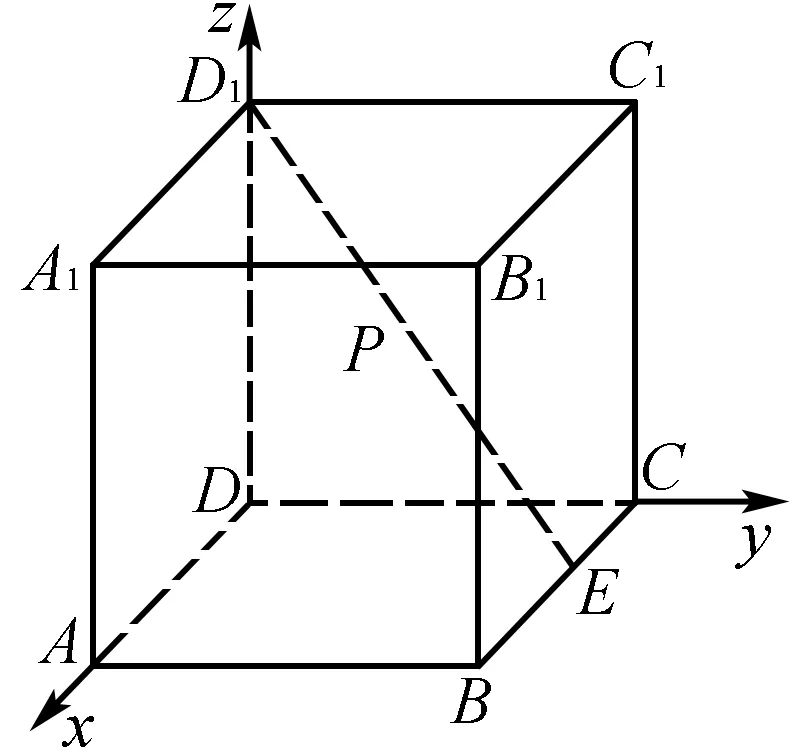
图5
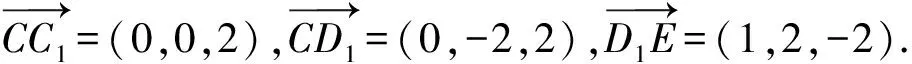
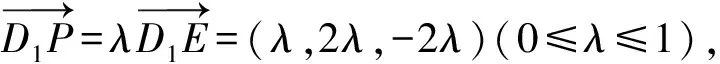
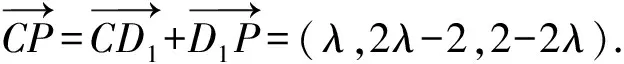
所以点P到直线CC1的距离
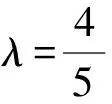
解法5 (向量法)建立空间直角坐标系同解法4,则D(0,0,0),D1(0,0,2),E(1,2,0).
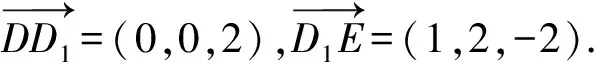
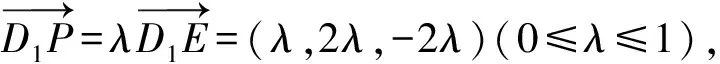

所以P(λ,2λ,2-2λ).
又设点P在CC1上的投影为点Q,
则Q(0,2,2-2λ).
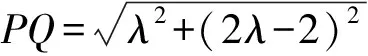
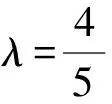
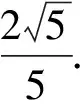
解法6(向量法)建立空间直角坐标系同解法4,则C(0,2,0),C1(0,2,2),D1(0,0,2),E(1,2,0).
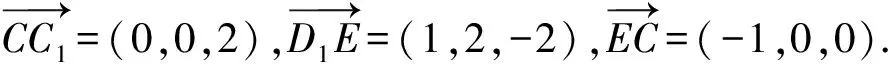
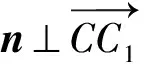
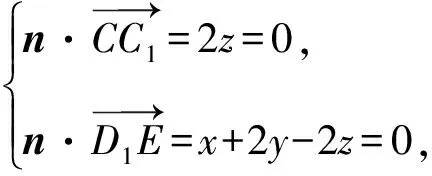

取x=2,则y=-1.
所以n=(2,-1,0).
所以异面直线CC1与D1E间的距离为
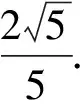
点评本题主要考查空间距离的求法,正方体的基本结构特征,以及空间线线、线面、面面平行和垂直的判定和性质等,体现了逻辑推理、直观想象和数学运算等核心素养.解题关键是熟练掌握各种距离之间的转化方法,属于中档题.
在上述六种解法中,前三种解法是纯几何方法,其中解法1把问题转化为求异面直线间的距离,利用定义法来解;解法2把问题转化为求点到平面的距离,利用等体积法来解;解法3把问题转化为点到直线的距离,利用等面积法来解.后三种解法是向量方法,通过建立空间直角坐标系,以向量为工具把几何问题转化为代数问题,这三种方法分别应用了点到直线的距离公式、两点间的距离公式和异面直线间的距离公式.
可以看出,空间距离的求法虽然很多,如定义法、转化法、等积法和向量法等,但始终渗透着数形结合思想和转化与化归思想.解题时应根据题设条件,灵活选择解法,优化解题过程.



