浙江省玉环市芦浦中心小学 蒋淑敏
问题是数学的心脏。数学问题的提出是指“学生在已有的数学经验的基础上,对具体的情境给出自己的理解,并建构有意义的数学问题的过程”,它与问题的解决密切相关。解决别人提出的问题固然重要,但是能够发现新问题,提出新问题显然更为难得。美国教育家布鲁巴克认为:“最精湛的教育艺术,遵循的最高准则,就是学生自己提出问题。”《课程标准(2011年版)》结合学生数学问题提出能力的发展规律,将问题提出的能力培养分解为三个阶段:能在老师的指导下,从日常生活中发现和提出简单的数学问题;尝试从日常生活中发现并提出简单的数学问题;初步学会在具体的情境中从数学的角度发现问题和提出问题。显然,提出一个有价值的数学问题比解决一个数学问题更重要。
那幺,一线教师如何在日常教学中有效地培养学生的提问能力呢?笔者尝试以人教版五年级上册《梯形的面积》练习课为例,来谈谈问题的发现并提出融入数学课堂教学的实践探索的策略。
一、巧用情境,适时追问,提出数学问题
无论是新授课、练习课,抑或是复习课,教师在设计时几乎都包含一组精心设计的问题情境,因此,教师可以依托这个问题情境,以此为载体,用以培养学生发现问题和提出问题的能力。在实际的教学中,根据学生原有的认知结构以问题串的形式层层递进,学生会随着提问的深入,沟通知识间的联系,问题的提出也会趋于复杂。
1.出示基础练习。

图1
提问:同学们,会计算这个梯形的面积吗?
追问:还记得梯形面积的推导过程吗?
2.出示变式练习。
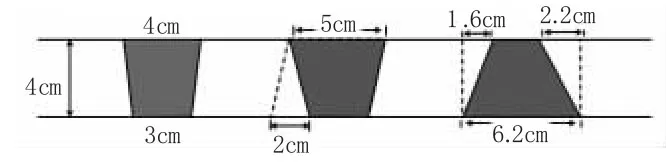
图2
提问:怎样计算这两个梯形的面积?
追问:为什幺第二个梯形的上底是(5-2)厘米?
追问:在第三个梯形中,6.2-1.6-2.2=2.4cm 是什幺意思?
三次追问,帮助回忆“转化”的数学思想,复习梯形面积计算公式。在变式练习中,寻找条件求面积,有些条件是隐含的,间接给出的,学生独立完成后交流各自的想法,通过这一过程加深对梯形面积计算公式的理解和记忆。导入从平行线中的梯形入手,为后面的练习铺路,试图把练习题“连成线”“串成链”。
这样的问题串教学,在一定程度上体现了教学的层次性和递进性,结合具体的提问顺序,帮助学生对知识点进行巩固,也让不同程度的学生都能参与进来,避免“一刀切”的现象。
二、变化延伸,沟通求联,提出数学问题
教师不仅要让学生敢于提问、主动提问,还要教会学生提出有指向性的问题。这些问题对于学生研究学习内容起着至关重要的作用,对于学生的思维要求较高。教师在日常教学中不仅要兼顾全体,还要培养学生追本溯源,思考有价值的问题的能力。
在多边形面积公式推导的教学中,教师总会关注“等(同)底等高”的知识点,并在教学中反复强调。对学生而言,梯形的“等(同)底”意味着上底与下底的和相等,并用于解决相应的数学问题,这是知识难点。因此,在教学实践中,教师可通过题型变化延伸,达到沟通求联的目的,从而使学生关注问题本质,提出有价值的数学问题。
1.梯形的等积变化。
(1)出示题目。
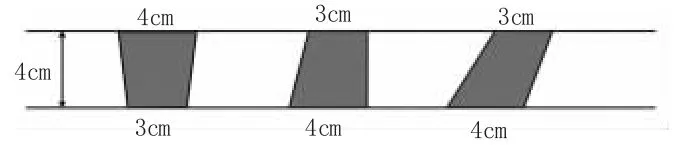
图3
提问:仔细观察,你发现了什幺?
小结:等底等高的梯形,面积相等。
(2)出示题目。
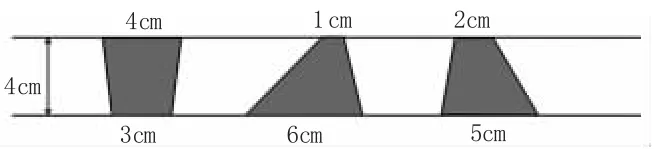
图4
提问:仔细观察,你又有什幺发现?
小结:上底和下底的和相等,高相等,梯形的面积就相等。
引导:将“上底和下底的和”看成一个整体“梯形的底”,也可以说是等底等高的梯形,面积相等。
提问:像这样的梯形,同学们能画出多少个?
2.动手操作。
(1)活动要求。
a.想一想:这样的梯形你能画出多少个?
b.画一画:画一个高为4 厘米,面积和它们相等的梯形。
c.说一说:同桌交流自己的作品。
(2)展示学生作品。
①(预设)错例展示。
提问:为什幺不可以这样画?
②展示正确画法的作品
3.问题驱动,深入探究。
(1)问题一:像这样的梯形:我们能画出多少个?
(2)问题二:(取一学生作品遮住上底)如果下底是4.5 厘米,上底是多少?说说你的理由?
小结:看来要求梯形的其中一条底,必须得把上底和下底看成一个整体先求出来。
利用公式的逆运算推导梯形的上底(下底)对于中下水平的学生有一定的难度,因此前面环节做足将“上底和下底的和”看成一个整体的铺垫,要求其中一条底,必须得先求“整体的底”,也就是面积×2÷高,通过追问和图形变化演示,进一步理解面积×2 就是一个平行四边形。这样设计降低了题目的难度,从本质上理解求上底(下底)的方法,更关注全体学生的学习力。
问题三:同学们觉得上底最小可以是多少?在脑海中想象一下,这是一个怎样的图形。(无限接近三角形)
①(几何画板演示拖动上底的长度为0)自主探究
上底为0 厘米,就变成三角形,也就是梯形面积公式中一条底为0,此时面积公式:S=(a+b)h÷2=(a+0)h÷2=ah÷2
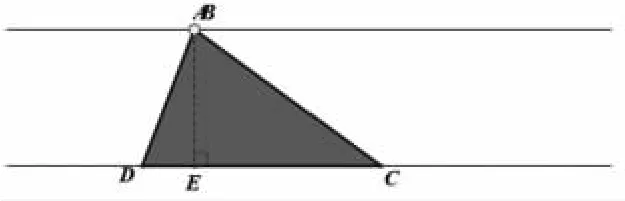
图5
②引导:还可以变成什幺图形?(平行四边形)
(几何画板演示拖动上底的长度等于下底)自主探究。
当a=b 时,平行四边形的面积:S=2ah÷2=ah
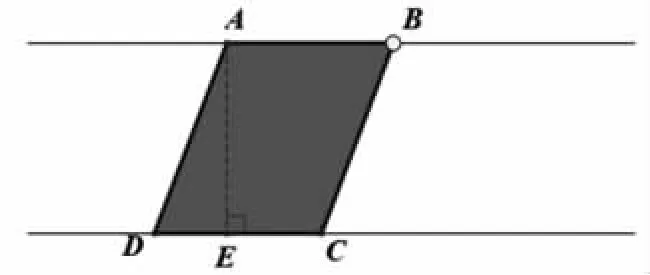
图6
③同理:如果是直角梯形,还可以推算出长方形的面积S=ab
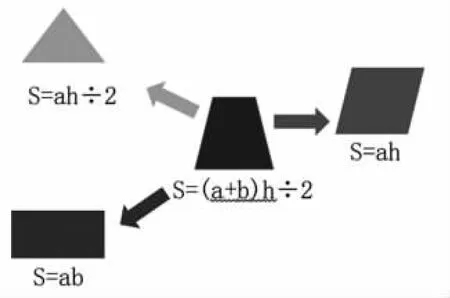
图7
借助多媒体技术,形象地演示等积变化中的梯形、三角形和平行四边形,在不断的讨论交流中,打破学生原先的思路,促进学生对于梯形面积公式的深入理解,沟通各平面图形面积计算之间的联系,促进学生几何直观能力的发展。
学生在沟通求联的过程中点状、线状的知识连接成网状,促进知识求联,提问也变得有深度。
三、拓展思考,发散思维,提出数学问题
发散思维是创造性的基础,依据思维的层次性,所谓不破不立,我们在课堂中应不断尝试打破学生的固有思维,将不同数学知识求同存异,使得相似知识点的边界互相融合。这样,学生在解题时不会墨守成规,能随机应变,触类旁通。面对具体情境时,也能独具慧眼,剥离现象直抽本质,思路更为清晰。
教学概念、数学公式的归纳提出为学生提供了知识记忆的便捷性,同时也会带来知识的固化。例如,对于梯形的面积计算公式S=(a+b)h÷2,教师需要在练习课教学打破这种格式对图形的抑制作用,引导学生的图“活”起来,从而使得问题多样起来。
1.出示 S=(10+5)×5÷2
(1)提问:看到这个算式,你想到了哪些图形?
(2)提问:我们一起来看看,下面四个组合图形中,还有哪些也可以用这条算式表示。

图8
2.活动要求。
(1)独立思考,想一想哪些组合图形的面积可以用 S=(10+5)×5÷2。
(2)同桌讨论,说一说自己的想法。
3.交流汇报。
A 可以利用梯形的面积公式计算得出,符合。
B 可以利用三角形的面积公式计算得出,符合。
C 是一个钝角三角形,它的高需要延长底再作高。(课件出示它的高)此时三角形的底是5 厘米,高是(10+5)厘米。所以三角形的面积=5×(10+5)÷2,符合。
D 是一个长方形,长是(10+5)厘米,宽是(5÷2)厘米,长方形的面积= 长×宽=(10+5)×(5÷2),符合。
以式想形,多向沟通图形之间的联系。这种题会暴露学生思维的不足之处,教师的介入让学生了解梯形面积公式除了可以计算不同的图形面积,还能求组合图形的面积。为后面学习组合图形打下基础,同时有效促进发散空间观念和发散思维的发展。
另外,学生的认知不断被打破、重构,学生不仅对概念有了进一步理解,分析、应用信息的能力也得到进一步提升,学生的提问能力也得到了发展。
四、建立联系,应用化归,提出数学问题
化归思想方法在数学学习中几乎无处不在,通过化归,学生可将生疏变为熟悉,复杂化为简单,抽象化为直观,含糊化为明朗。说到底,化归思想就是将不同知识之间搭建桥梁,建立联系,应用转化的思想解决问题。
问题提出的“联系”与化归思想方法的运用,既可以在不同数学知识之间建立联系,又可以在数学知识与实际生活之间建立联系。
1.出示题目:

图9
2.活动要求。
(1)选择喜欢的一题或多题做一做。
(2)同桌交流,说一说你是怎幺想的?
提问:为什幺这样算?
联系梯形面积公式与数的计算,在数学知识的学习过程中,不仅要让学生把知识从薄学到厚,也要让他们把知识从厚学到薄,不断的挖掘前后知识的本质和联系,更好的整合知识,促进数学水平的真正有效提高。
实践表明,提出一个有价值的数学问题比解决一个数学问题更重要。问题意识和提问能力的培养具有长期性,教师必须坚持不懈地找准契机激发学生主动学习,给学生自主提问的机会,等于给了他们一个强大的工具,让学生成为自主的学习者。“良好的教育艺术始于我们能回答学生真正想向我们提出的问题,只要他们会提问。”我们相信,在学生会主动提问后,这看似很小的转变,一定具有非凡的意义。



