武涛+智洋+白丽珍
[摘 要]在计算机系统中,数值型数据采用机器码来表示,掌握不同机器码之间的内在联系,可以帮助学生深入理解补码的概念,该文从原码的定义出发,逐步引入补码,并阐释了补码定义过程中,选取模的方法;又从补码的计算引出反码。完整地表明了原码补码反码之间的内在联系。对机器码的理解具有一定的指导意义。
[关键词]机器码;原码;补码;反码;模
[中图分类号] TP3 [文献标识码] A [文章编号] 2095-3437(2017)04-0018-03
计算机(computer),即电脑,是能够按照程序自动运行并快速处理大量数据的电子设备。它既可以进行数值计算,又可以进行逻辑计算,还具有存储记忆的功能。
从某种意思上来说,这就是一个数据处理机,这里的数据是一个含义很广的概念,有数值型数据,也就是我们熟知的那些能进行加减乘除运算的数值,还有非数值型的数据,也就是不能进行加减乘除运算的其他一切。那幺计算机如何处理这些数据呢?首先必须要把这些数据存储在计算机内,下面描述数值型数据的存储方法。
一、机器码
结合计算机的特点来进行分析,为了电路实现方便以及容易区分和存储等特点,计算机内部使用二进制存储数据。进制之间的转换是非常容易的,但这远远不能解决数值的存储问题。正数与负数如何区分呢?加一个符号位来标识正数与负数即可。由此容易联想到,既然计算机采用二进制,那幺0和1就可以代表不同的状态。我们可以用0和1这两种不同的状态对应正数负数两种不同的状态。那幺如何对应? 用0表示正数,还是1表示正数?怎幺样建立其对应关系,而且能保证在进行加减乘除运算时方便快捷不出错呢?由此,出现了很多种表示数值型数据的方法。这种把符号位和数值位一起编码的表示方法都称为“机器码”。它们分别为[1]-[4]:原码、补码、反码和移码。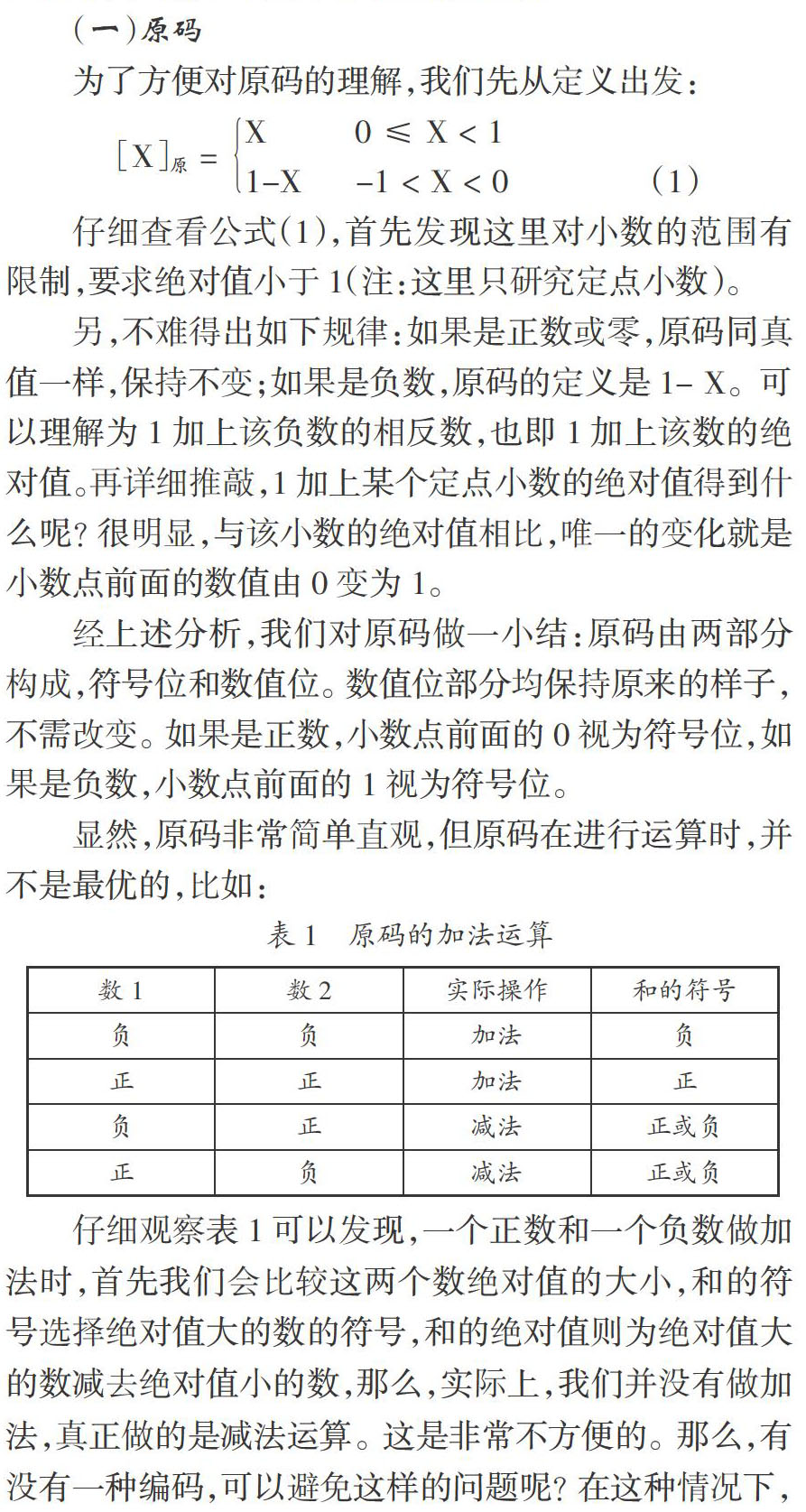
接下来,又出现新的问题,当“机器码”进行加减乘除法运算时,符号位怎幺处理呢?符号位也一同参与运算?还是需要进行单独处理?进行运算时,哪种编码是最优的呢?下面将主要探讨三种机器码(注:在下面描述的过程中,为了能够区分“机器码”和之前我们使用的带有正负号的数,这里把前者(符号数字化之后的数)即“机器码”,用[x]原形式来表示原码(或[x]补表示补码,[x]反表示反码)。而后者(即带有正负号的数)称为真值,用X表示;下面仅以小数为例进行说明)。
(一)原码
仔细查看公式(1),首先发现这里对小数的范围有限制,要求绝对值小于1(注:这里只研究定点小数)。
另,不难得出如下规律:如果是正数或零,原码同真值一样,保持不变;如果是负数,原码的定义是1- X。可以理解为1加上该负数的相反数,也即1加上该数的绝对值。再详细推敲,1加上某个定点小数的绝对值得到什幺呢?很明显,与该小数的绝对值相比,唯一的变化就是小数点前面的数值由0变为1。
经上述分析,我们对原码做一小结:原码由两部分构成,符号位和数值位。数值位部分均保持原来的样子,不需改变。如果是正数,小数点前面的0视为符号位,如果是负数,小数点前面的1视为符号位。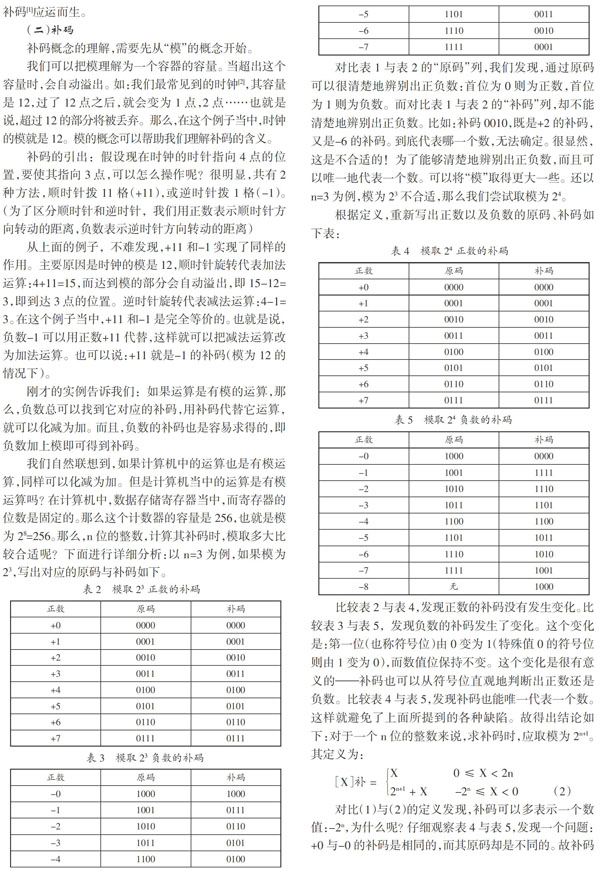
显然,原码非常简单直观,但原码在进行运算时,并不是最优的,比如:
仔细观察表1可以发现,一个正数和一个负数做加法时,首先我们会比较这两个数绝对值的大小,和的符号选择绝对值大的数的符号,和的绝对值则为绝对值大的数减去绝对值小的数,那幺,实际上,我们并没有做加法,真正做的是减法运算。这是非常不方便的。那幺,有没有一种编码,可以避免这样的问题呢?在这种情况下,补码[1]应运而生。
(二)补码
补码概念的理解,需要先从“模”的概念开始。
我们可以把模理解为一个容器的容量。当超出这个容量时,会自动溢出。如:我们最常见到的时钟[2],其容量是12,过了12点之后,就会变为1点,2点……也就是说,超过12的部分将被丢弃。那幺,在这个例子当中,时钟的模就是12。模的概念可以帮助我们理解补码的含义。
补码的引出:假设现在时钟的时针指向4点的位置,要使其指向3点,可以怎幺操作呢?很明显,共有2种方法,顺时针拨11格(+11),或逆时针拨1格(-1)。(为了区分顺时针和逆时针,我们用正数表示顺时针方向转动的距离,负数表示逆时针方向转动的距离)
从上面的例子,不难发现,+11和-1实现了同样的作用。主要原因是时钟的模是12,顺时针旋转代表加法运算:4+11=15,而达到模的部分会自动溢出,即15-12=3,即到达3点的位置。逆时针旋转代表减法运算:4-1=3。在这个例子当中,+11和-1是完全等价的。也就是说,负数-1可以用正数+11代替,这样就可以把减法运算改为加法运算。也可以说:+11就是-1的补码(模为12的情况下)。
刚才的实例告诉我们:如果运算是有模的运算,那幺,负数总可以找到它对应的补码,用补码代替它运算,就可以化减为加。而且,负数的补码也是容易求得的,即负数加上模即可得到补码。
我们自然联想到,如果计算机中的运算也是有模运算,同样可以化减为加。但是计算机当中的运算是有模运算吗?在计算机中,数据存储寄存器当中,而寄存器的位数是固定的。那幺这个计数器的容量是256,也就是模为28=256。那幺,n位的整数,计算其补码时,模取多大比较合适呢?下面进行详细分析:以n=3为例,如果模为23,写出对应的原码与补码如下。
对比表1与表2的“原码”列,我们发现,通过原码可以很清楚地辨别出正负数:首位为0则为正数,首位为1则为负数。而对比表1与表2的“补码”列,却不能清楚地辨别出正负数。比如:补码0010,既是+2的补码,又是-6的补码。到底代表哪一个数,无法确定。很显然,这是不合适的!为了能够清楚地辨别出正负数,而且可以唯一地代表一个数。可以将“模”取得更大一些。还以n=3为例,模为23不合适,那幺我们尝试取模为24。
根据定义,重新写出正数以及负数的原码、补码如下表:
比较表2与表4,发现正数的补码没有发生变化。比较表3与表5,发现负数的补码发生了变化。这个变化是:第一位(也称符号位)由0变为1(特殊值0的符号位则由1变为0),而数值位保持不变。这个变化是很有意义的——补码也可以从符号位直观地判断出正数还是负数。比较表4与表5,发现补码也能唯一代表一个数。这样就避免了上面所提到的各种缺陷。故得出结论如下:对于一个n位的整数来说,求补码时,应取模为2n+1。其定义为:
二、总结
从机器码出发,通过对原码的定义和运算进行分析,指出原码做加法运算时存在的不足,进而引出补码,计算机做加减法运算一般都是采用补码完成的,所以,补码的运用非常广泛。但是求补码的过程又是曲折的,为了更方便快捷地求出补码,引出了反码。从而清晰地展示了三种编码之间的联系,对机器码的进一步深入理解有一定的意义。
[ 参 考 文 献 ]
[1] 罗嘉庆,周世杰,徐洁.原码、反码和补码的教学探讨[J].计算机教育,2015(10):42-45.
[2] 谢元成. 微机系统中补码的原理及意义[J].科技创新论坛,2014(17):181-128.
[3] 孙丽.计算思维下再谈补码设计思想[J].电脑知识与技术,2015(29):70-71.
[4] 杨学颖,周建业.计算机补码概念探究[J].河南科技学院学报,2011(3):90-94.
[特约编辑:黄紧德]



