张弛


[摘 要] 研究一元线性回归问题的可视化教学案例。基于GeoGebra平台,通过一个具体的实际教学案例研究不同函数模型拟合效果、函数拟合的残差比较等,实现一元线性回归问题的教学可视化,并在与传统教学设计对比后得出可视化教学具有有效增强教学效果、提高学生学习积极性的结论。
[关 键 词] 教学设计;GeoGebra;可视化
[中图分类号] G712 [文献标志码] A [文章编号] 2096-0603(2021)45-0158-02
对于初识统计学问题的职业学校学生来说,回归分析问题的学习对初等函数知识要求较高,且具有计算量较大、思维抽象的特点。GeoGebra是一款动态数学软件,同时具备代数变量运算、统计概率以及3D绘图等实用功能。GeoGebra软件通过便捷计算代数系统和智能指令输入系统,真正实现了数与形的融合,将抽象的数据关系可视化为可具体感知的图像信息,激发中职生数学的学习兴趣,提升学生的数学核心素养。
一、教材解读
(一)教学目标与教学重难点
“一元线性回归”是江苏职业学校文化基础课数学第十章第八节的内容。其教学重点是了解一元线性回归的基本思想与方法,难点是理解回归模型建立的基本步骤。
(二)传统教学设计流程
茶水销售问题:商店为了解茶水销售量与最低气温之间的关系,随机统计并制作了某六天的销售量(单位:杯)与当天最低气温(单位:℃)的对照表(见表1)。
若某一天最低气温为-5℃,能否估计这天商店卖出茶水的杯数?
在教材中,以此题作为引入问题,要求建立茶水销售量y关于气温x的一元线性回归方程。从传统教学设计的角度,此题包括以下三个问题的讨论与解决:(1)作出热茶销售量与气温的散点图,根据散点图建立它们间的函数关系;(2)建立以温度为自变量、茶水销售杯数为因变量的一元线性回归模型,计算残差并利用残差进行数据分析;(3)计算W(a,b),并利用最小二乘法对建立的模型进行分析,判断能否较好地刻画温度和茶水销售量间的数量关系,最终生成一元线性回归方程。
二、基于GeoGebra平台的教学过程
GeoGebra软件具有数据统计与分析、函数绘图和强大的代数运算功能,故我们利用GeoGebra软件,针对该课题实施教学活动。
(一)建立一元线性回归模型环节
1.绘制散点图
启动GeoGebra软件后,在主菜单栏中的“视图”选项里单击“表格区”,则在界面右侧弹出表格区。然后,在表格区输入表1中的“最低气温”“茶水销售量”及对应数量。接着,框选数据,通过右键弹出对话框,选择对话框中的“创建”—“点列”栏目。此时,绘图区内生成数据散点图,即生成点列为l1。
教师在生成散点图后,再呈现教材中的散点图,由学生对两张图片进行对比,分析两张图片的区别,再总结汇报,教师进行点评。学生会发现教材中的坐标系的纵轴已经进行了缩放,散点分布失真。那么,散点分布的规律到底满足什么样的特征?仅仅依靠直观印象是不能做出正确的判断的,由此学生探究的愿望渐浓,期待进行下一步的探究。
2.建立一次函数模型环节
散点图生成后教师指导学生观察其特征,回顾已掌握的函数图像,由学生猜想并尝试建立回归模型。在小组讨论后汇报的过程中,大部分学生都能得出“散点图分布在一条直线附近”的结论,也会有一部分学生猜想二次函数、幂函数的情况。针对这一情况,教师要及时给予表扬,引导学生先尝试建立一次函数回归模型,并将其他情况作为拓展任务暂不展开。
首先,教师指导学生在指令栏里输入“多项式拟合”,弹出“多项式拟合(<点列1>,<多项式次数>)”指令提示。
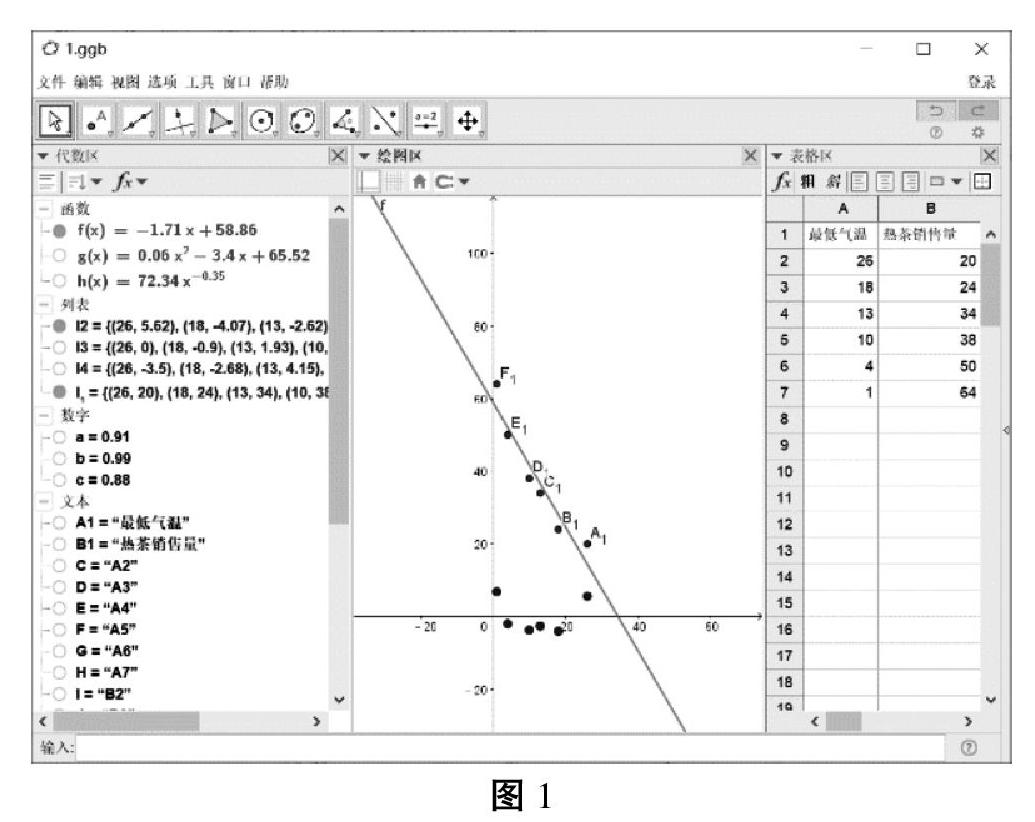
接着,将其中“<点列1>,<多项式次数>”改为“l1,1”,并点击回车后,此时在绘图区中生成一次函数图像f(x),同时在代数区内显示函数f(x)=-1.71x+58.86,在计算机生成一次回归函数后,教师则呈现回归直线的数学定义:用直线方程近似表示的相关关系叫作线性关系,这条直线成为回归直线,其中a,b称为回归系数。学生回答出计算机生成的回归系数为“a=1.71,b=58.86”。
3.一次函数模型残差分析环节
教师指导学生在指令区内输入“残差图”,弹出“残差图(<点列>,<函数>)”,将其改为“残差图(l1,f(x))”,则在绘图区内呈现出一次函数模型的残差图。(如图1所示)。
在残差图的直观演示下,教师引导学生将残差与方差进行对比,促进学生对残差这一概念的理解。然后,教师再借助残差图,简要介绍残差的平方和表达式以及求解回归系数的最小二乘法。最后,给出一元回归直线的系数计算公式。
(二)回归模型拓展环节
1.建立二次函数、幂函数模型环节
教师依据学生猜想的另外两种回归模型:二次函数与幂函数模型,指导学生自主完成计算机绘图任务。首先,教师指导学生在指令栏里输入“多项式拟合”,弹出“多项式拟合(<点列1>,<多项式次数>)”指令提示。接着,将其中“<点列1>,<多项式次数>”改为“l1,2”,并点击回车,此时绘图区中生成二次函数的函数图像g(x),并且代数区内会呈现函数g(x)=0.06x2-3.4x+65.52。然后,在指令栏里输入“幂函数”,弹出“幂函数拟合(<第一象限点列1>)”指令提示。接着,将其中“<第一象限点列1>”改为“l1”,并点击回车,此时在绘图区中生成幂函数图像h(x),同时在代数区内显示函数h(x)=72.34x-0.35。
2.不同函数模型拟合效果的比较
教师指导学生作出二次函数与幂函数模型的残差图。通过学生先观察、讨论,再分析比较,发现二次函数模型的残差分布于x轴附近,残差绝对值也较小;幂函数模型残差在x轴附近分布较为分散,即残差绝对值较大,所以得出结论:二次函数模型拟合较幂函数模型好。但学生也会提出质疑:“仅凭直观感知,没有计算”是不能作为充分条件的。
因此,教师顺势指导学生利用R2值验证猜测结论。
首先,在指令栏里输入关键词“可决系数”,提示“可决系数R方(<点列1>,<函数>),将其中“<点列1>,<函数>”改为“l1,f(x)”,单击回车键后,在代数区内显示a=0.91(即R2=0.91)。
然后,在指令栏里输入关键词“可决系数”,提示“可决系数R方(<点列1>,<函数>),将其中“<点列1>,
<函数>”改为“l1,g(x)”,并单击回车键,在代数区内显示b=0.99(即R2=0.99)。
最后,在指令栏里输入关键词“可决系数”,提示“可决系数R方(<点列1>,<函数>),将其中“<点列1>,
<函数>”改为“l1,h(x)”,再单击回车键,在代数区内显示c=0.88(即R2=0.88)。
在对三种函数拟合情况的“可决系数”进行比较分析时,教师可以向学生明确R2越大表示拟合效果越好。
观察函数的图像与相应R2值的大小对比,师生可以发现二次函数模型拟合的效果最佳,经比较甚至比教材中提供的一次函数模型拟合的效果更为精密,但是幂函数模型的拟合效果是三者中最差的。再将三种模型刻画在同一坐标系之中则更具视觉直观性(如图2所示)。故而可以借助二次函数解析式对-5℃的情况预测小卖部卖出茶水的杯数。
三、两种教学设计效果分析
基于GeoGebra软件的教学设计,给课堂教学创设了一个学生大胆猜想、自主探索、即时生成的学习情境。首先,本次课的设计节省了学生手动作图及计算的时间,学生参与思考、交流讨论的意识得到加强。其次,相比传统的教学设计,本次设计拓展了二次函数与幂函数模型的探究,这产生于GeoGebra软件可视化效果作用下的课堂即时生成。最后,相比较传统教学设计中直接引入残差平方值的计算,GeoGebra软件中残差图的运用更具直观性,有利于学生从直观感知过渡到理性认知,进一步进行针对几种函数模型进行主动解构与对比。所以,本课题的教学设计中生成的二次函数拟合程度较好的结论,是相对于教材中一次函数模型更加合理的一种函数模型的呈现,是一种机智的教学生成。
参考文献:
[1]张志勇.高中数学可视化教学:原则、途径与策略:基于GeoGebra平台[J].数学通报,2018,57(7):21-24,28.
[2]张维忠,唐慧荣.可视化教学内容设计的五大原则[J].电化教育研究,2010(10):99-102.
[3]李红美,王镇国,韦俊楠.面向移动终端课堂互动信息的可视化分析:以高中数学为例[J].现代教育技术,2017,27(2):113-119.
◎编辑 郑晓燕



