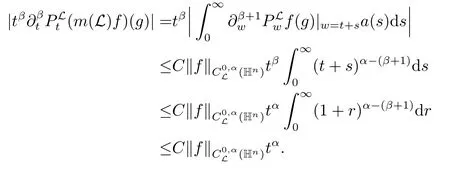孙传红,李澎涛
(青岛大学数学与统计学院,山东 青岛266071)
1.引言
令L=-ΔHn+V 为Heisenberg群Hn上的Schrdinger算子,其中ΔHn为Heisenberg群Hn上的次Laplace算子,非负位势V 属于逆Hlder类BQ/2,这里Q为Heisenberg群Hn的齐次维数.Heisenberg群Hn在Lie群上的底流形是R2n× R,它的乘积为(x,t)(y,s) = (x + y,t + s +它的左不变向量场的Lie代数为
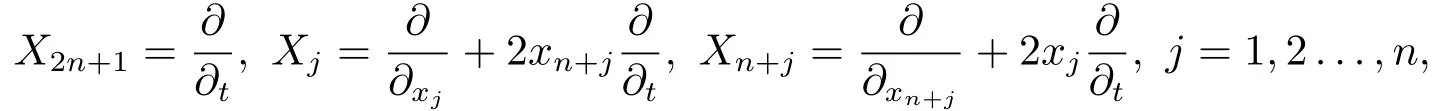
这里所有非平凡关系为[Xj,Xn+j] = -4X2n+1,j = 1,2...,n.次Laplace算子ΔHn定义为梯度∇Hn定义为∇Hn=(X1,...,X2n).
Hn上的伸缩为δr(x,t) = (rx,r2t),r >0,左不变距离为d(η,g) = |η-1g|,那么以g为球心,r为半径的球可以表示为
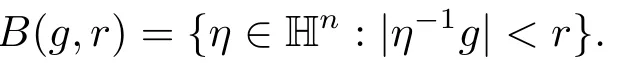
球的体积为|B(g,r)|=cnrQ,这里并且Q=2n+2为Hn的齐次维数.
设V 是一个Hn上非负局部Lq可积函数,如果对Hn上的每个球B,都存在C >0使得逆Hlder不等式
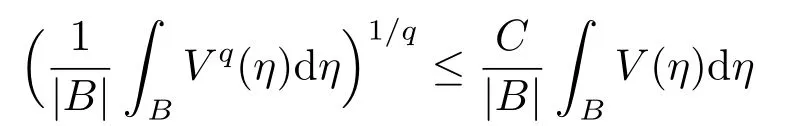
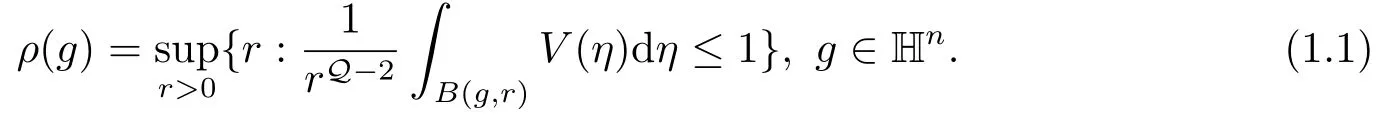
性质1.1[1]存在C >0和m0≥1使得对任意的Hn上的g和η,有
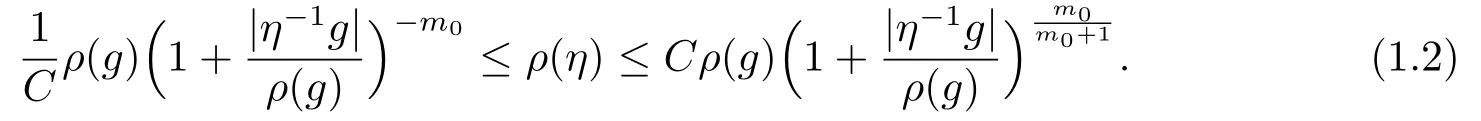
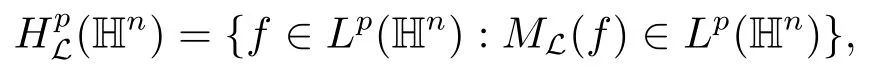
在文[11]中,MA等人得到了Rn上与Schrdinger算子有关的Poisson核正则性估计,本文中,我们将其推广到Hn上.
定义1.1Hn上的一个连续函数f属于(Hn),0 <α ≤1,如果
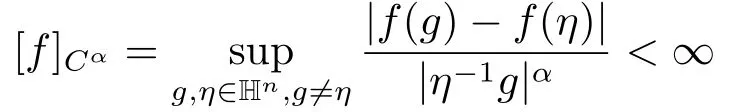
且
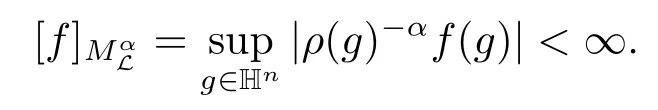
令Un是在Cn+1上的Siegel上半空间,
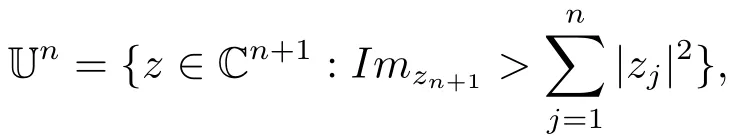
这里Un全纯等价于Cn+1中的单位球.Heisenberg群Hn是Un的一个自同构的幂零子群.Heisenberg群Hn也可以用边界∂Un定义[12].我们用Heisenberg坐标(g,t) = (x,s,t)来表示在Un上的点,这里
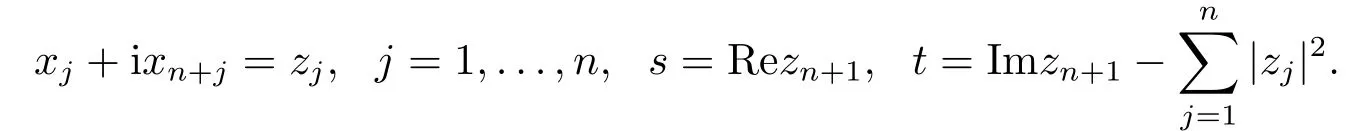
对于Hn上的任意球B =B(g,r),我们定义在球B上的Carleson方体Ω(g,r)为
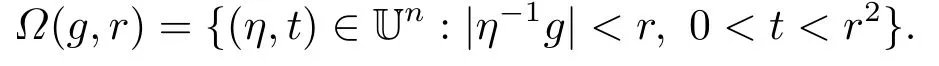
如果Un上的一个非负的Borel测度µ满足
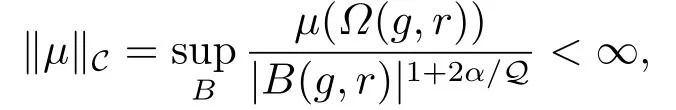
则称µ为分数阶的Carleson测度.
下面我们给出与L相关的BMO型空间.
定义1.2一个局部可积的函数f属于(Hn),0 ≤α ≤1,如果存在一个常数C使得
注1.1如果0 <α ≤1,那么和是等价的,参见文[13].
2.主要定理及其证明
设β是一个正数,m = [β] + 1表示大于β的最小整数.令F(g,t)是一个函数,其中g ∈Hn和t >0.类似于[14],我们定义
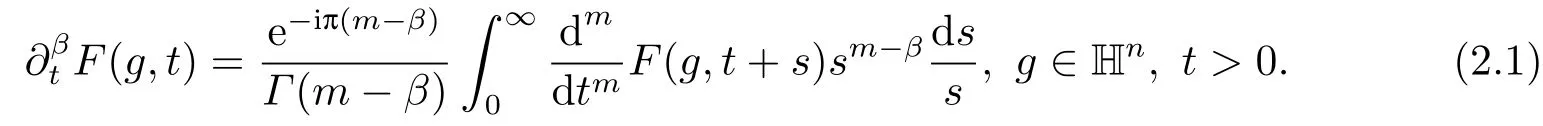
本文我们用Γ和B分别表示Gamma函数和Beta函数.
引理2.1令0 <γ <1,f是一个连续函数,并且使得|f(g)|≤Cρ(g)γ,这里ρ是在(1.1)中定义的辅助函数.那么有
(i) 对任意的ε >0,函数f(g)(1+|g|)-(Q+γ+ε)可积;
(ii) 对任意的β >γ和N >0,存在一个常数Cβ,N,f使得
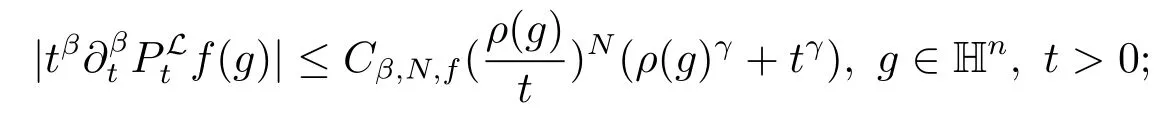
(iii) 对任意的N >0,存在一个常数CN,f使得

证对于(i),只需证明积分
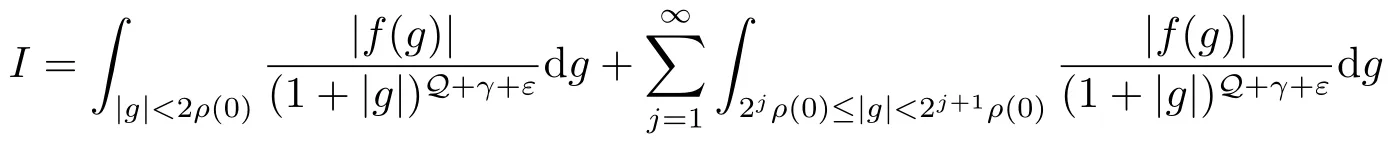
是有限的.通过不等式(1.2),我们得到ρ(g)≤Cρ(0)2j,因此
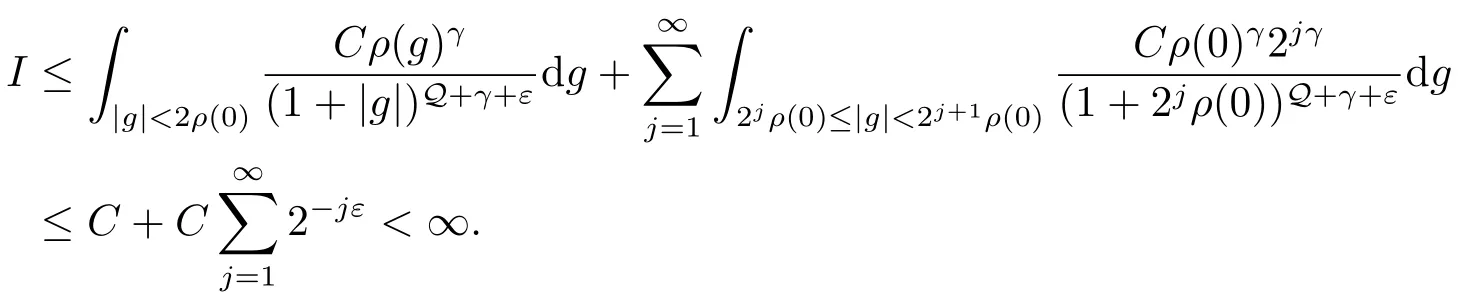
对于(ii),由命题2.1(b)和引理1.1,对于常数C =Cβ,N,f,我们有
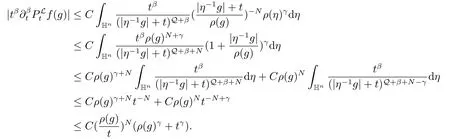
(iii) 可以类似的证明,这里我们略去细节.
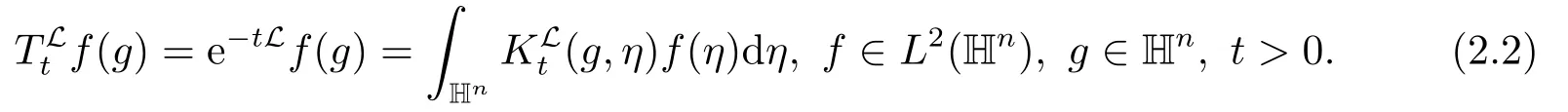
引理2.2[1]对于任意的N >0,存在一个常数c,并且对于每一个N都有一个常数CN>0使得
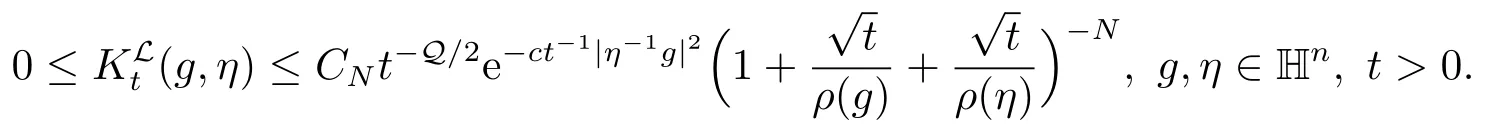
令
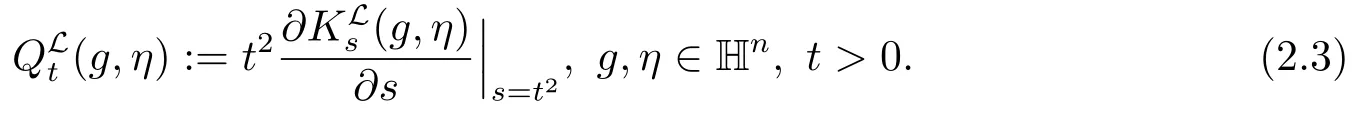
引理2.3[1]令δ =2-Q/q ∈(0,1),存在一个常数c,并且对于每一个N都有一个常数CN使得
(i)
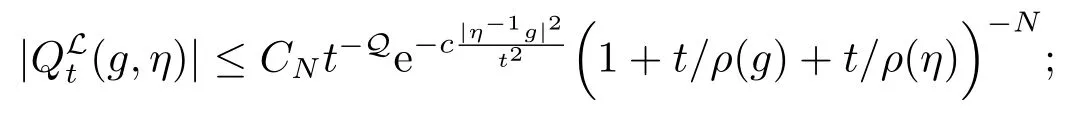
(ii) 对所有|u|≤t,
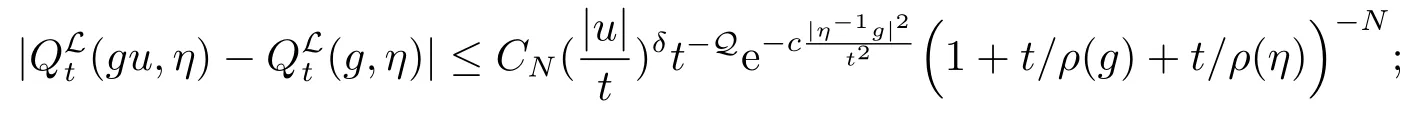
(iii)
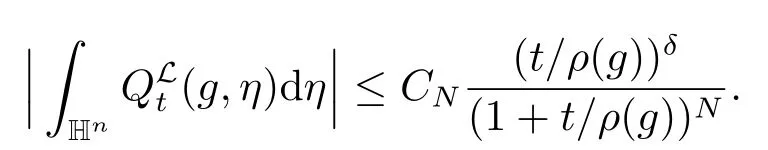
注2.1令0 <δ′≤δ,从引理2.3(iii)可以得到对于任意的N >0,存在一个常数CN使得
通过(2.2)式和参考文[15]中的Bochner从属公式,我们有

对于任意的g ∈Hn,t >0,Poisson核可以表示为
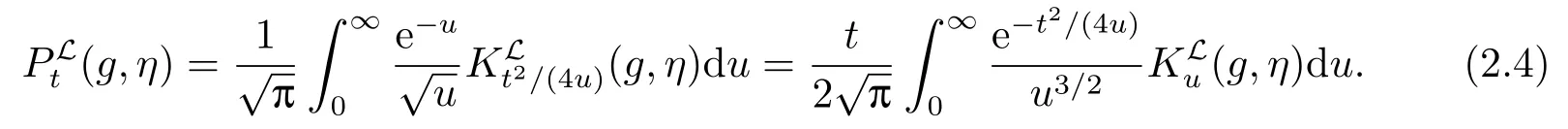
下面通过(2.1)计算Poisson核的分数阶导数,我们利用Hermite多项式Hm(r),这里m ∈通过(2.3)和(2.4),可得
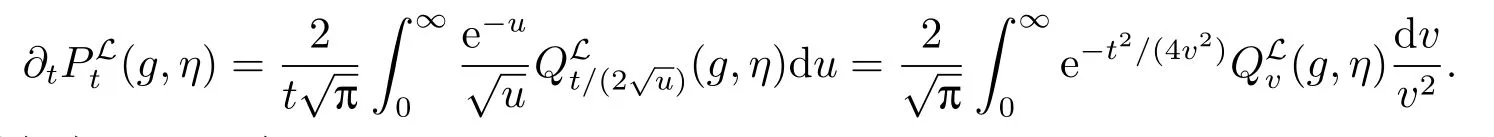
因此,对任意m ≥1,有
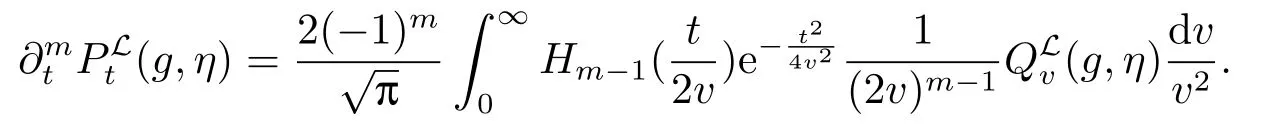
由β >0和m=[β]+1,我们可以得到
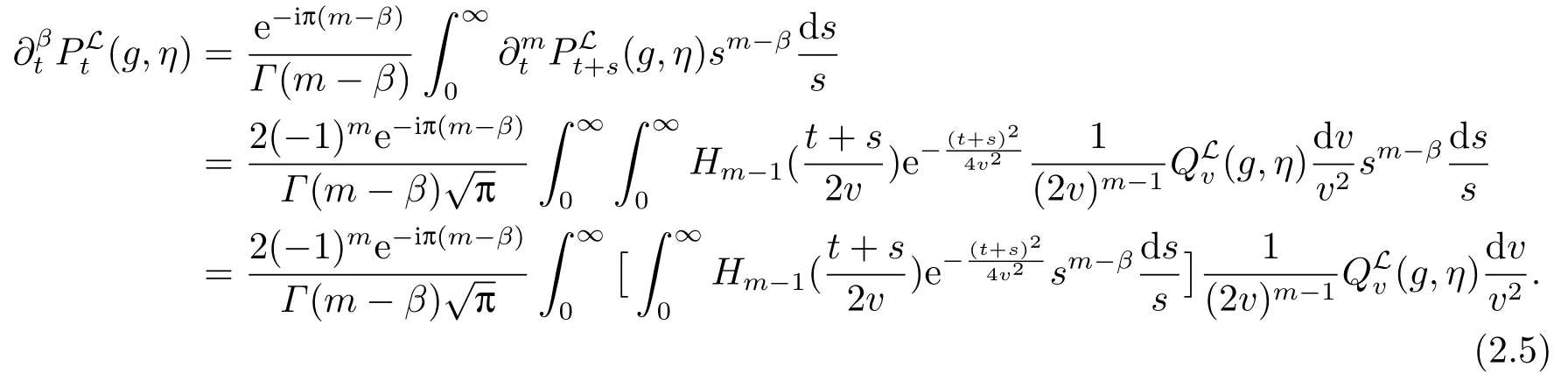
命题2.1令β >0,对任意的0 <δ′≤δ,0 <δ′<β和N >0,存在一个常数C = CN,β,δ′,使得
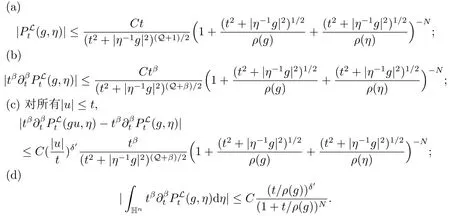
证首先证明(a),通过(2.4)的第二个等式和引理2.2,可以得到
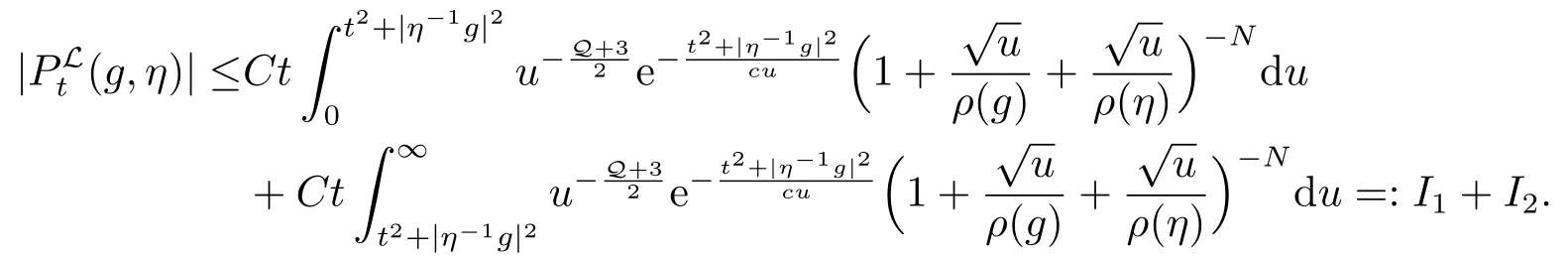
对于I1,进行变量替换: z =(t2+|η-1g|2)/u,我们有
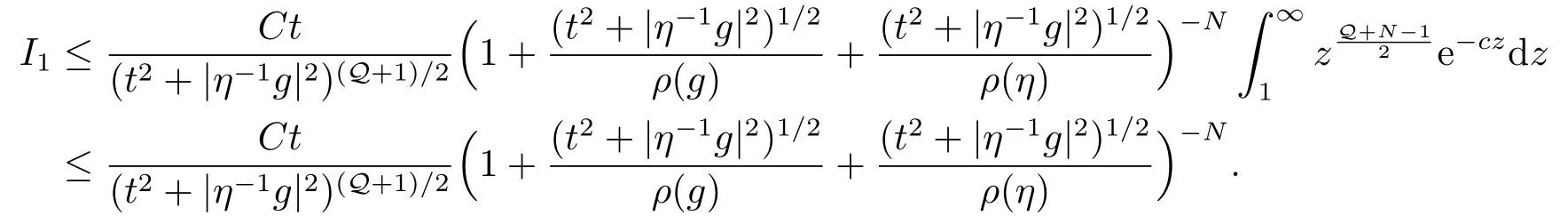
对I2,有
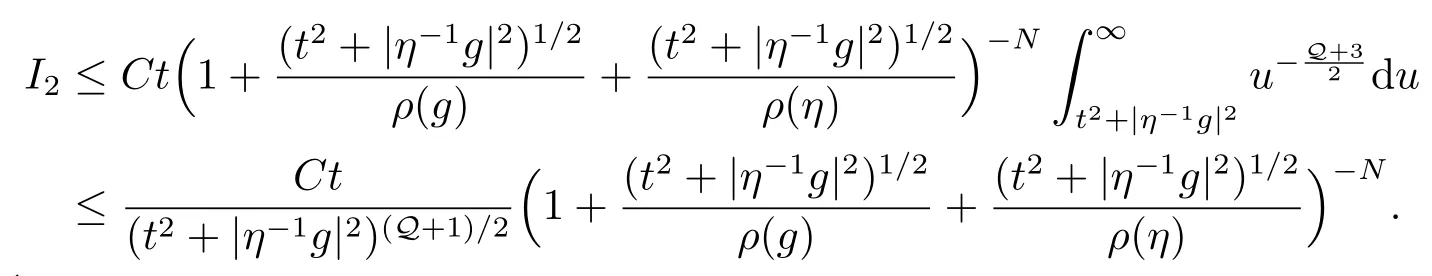
故(a)得证.
下面证明(b),我们估计在(2.5)中括号里的积分
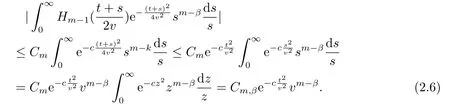
通过(2.5)和引理2.3(i),可得
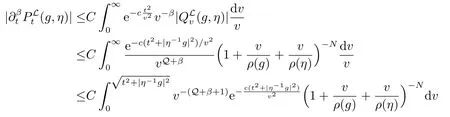

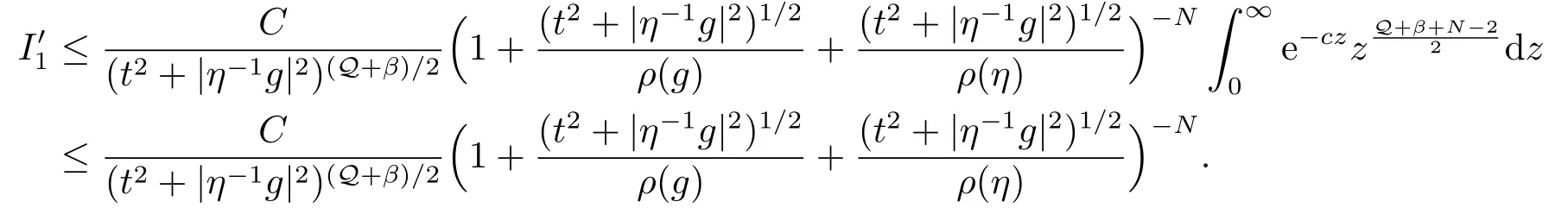
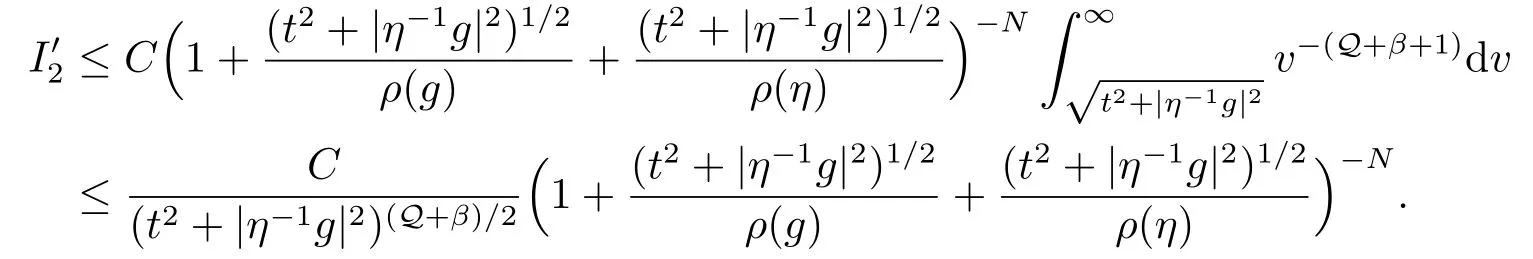
这就证明了(b).
对于(c),通过(2.5)和(2.6)式的估计,以及引理2.3(ii),可得
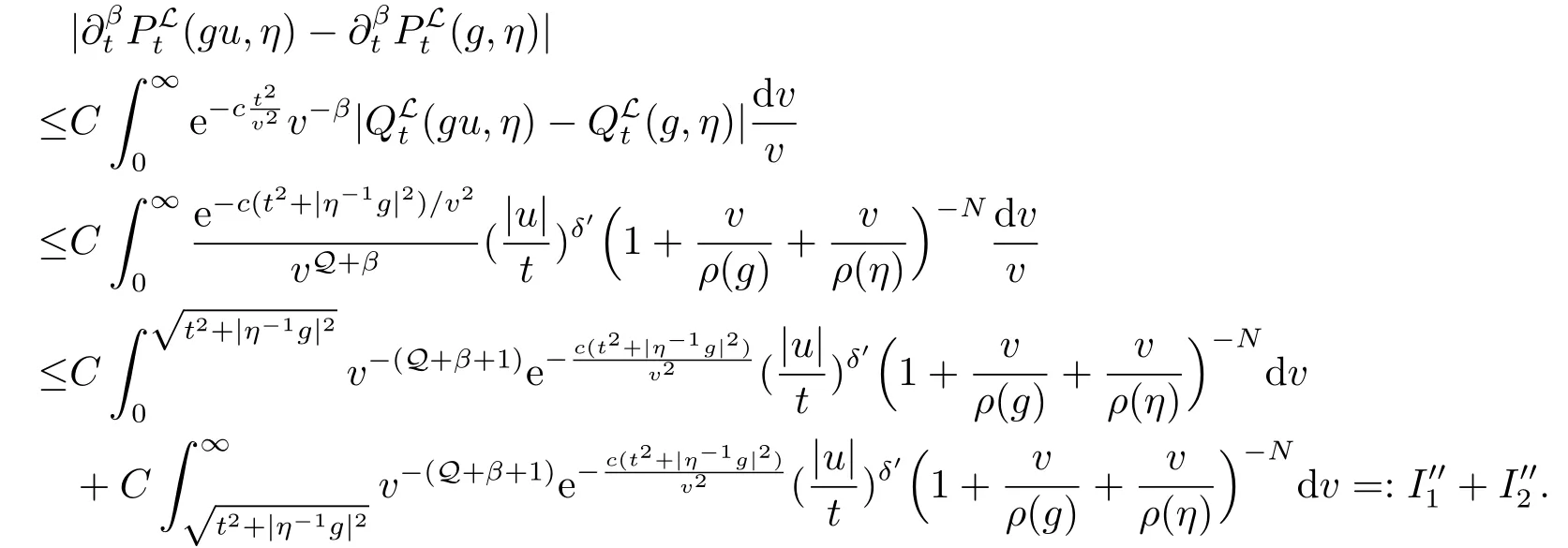
对于(d),令0 <δ′≤δ和0 <δ′<β,通过注2.1和变量替换: w =t/v,可得
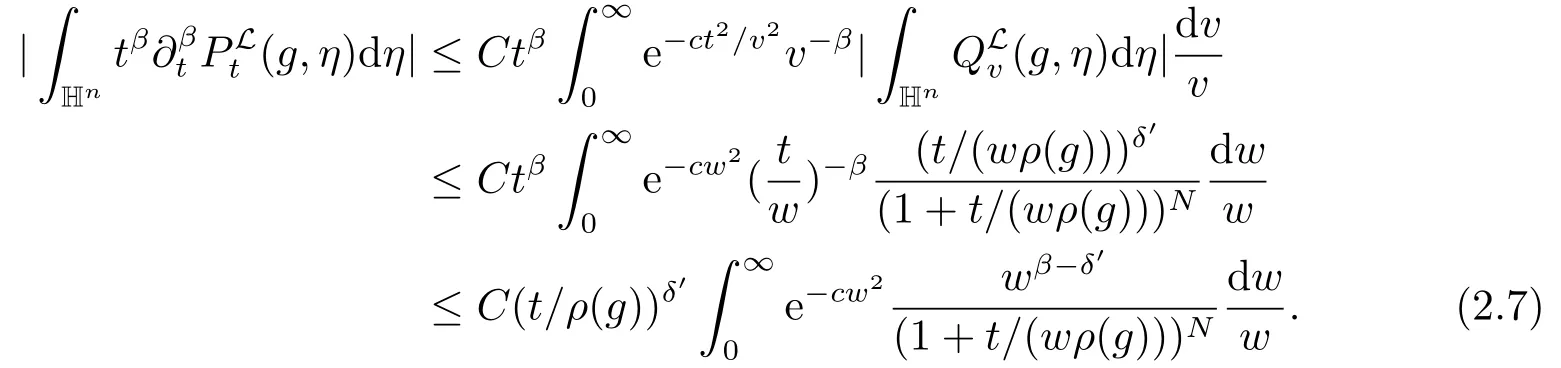
我们把(2.7)式中的积分分为两部分,一方面,
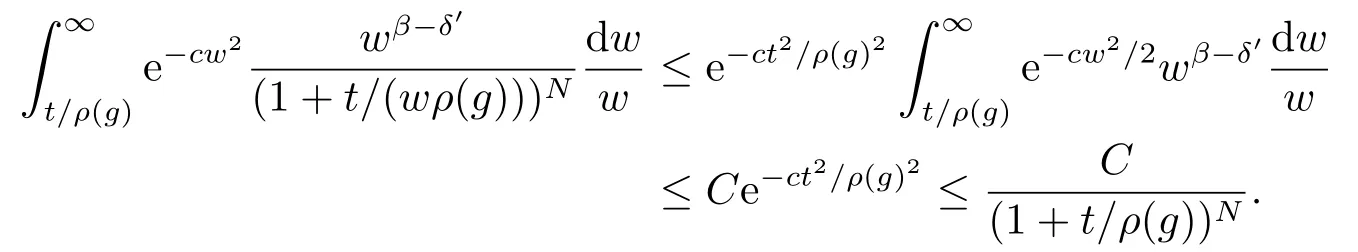
另一方面,我们分两种情况讨论.当t/ρ(g)≤1时,有

当t/ρ(g)>1时,可得
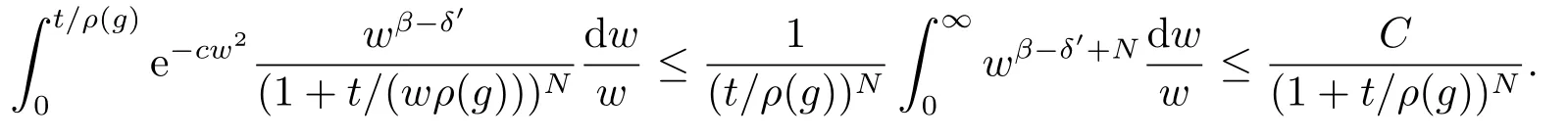
因此,(d)成立.
引理2.4算子从L2(Hn)到是等距的,并且有
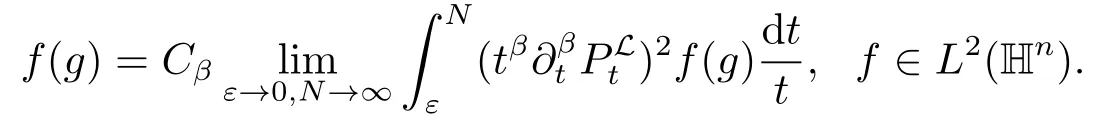
命题2.2令f ∈0 <α ≤1,B = B(g,r),其中r <ρ(g),那么存在一个常数C =Cα使得
证设j0是一个正整数,使得2j0r ≤ρ(g)<2j0+1r,因为所以有

注2.2从命题2.2的证明可以看出,如果f属于BMOL(Hn)=(Hn),B =B(g,r)和r <ρ(g),我们有
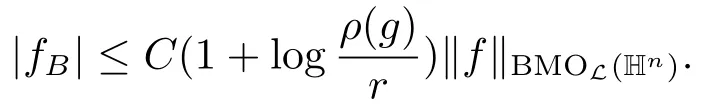
在文[10]中,YANG等证明了如下函数空间的对偶关系.
定理2.1令q >Q和0 ≤α <1,则的对偶空间是
类似于[11]中的结果,我们可以得到如下BMO型空间的等价刻画.
定理2.2令0 <α <1,f是一个使得对任意ε >0,都有f(g)(1+|g|)-(Q+α+ε)可积的函数,当β >α,q >Q时,下面的叙述是等价的:
(ii) 存在一个常数c1,β使得
(iii) 存在一个常数c2,β使得对Hn上所有的球B =B(g0,r),令={(g,t): g ∈B,0 <t ≤r},有
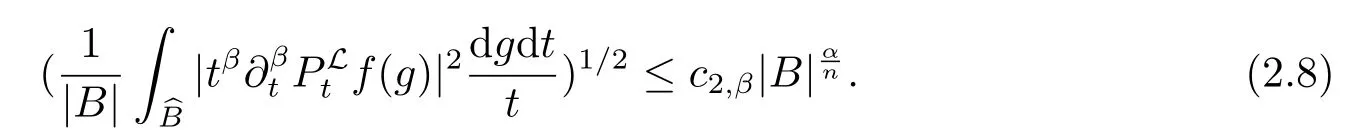
证证明(i)⇒(ii).令我们有

通过命题2.1(b),可得
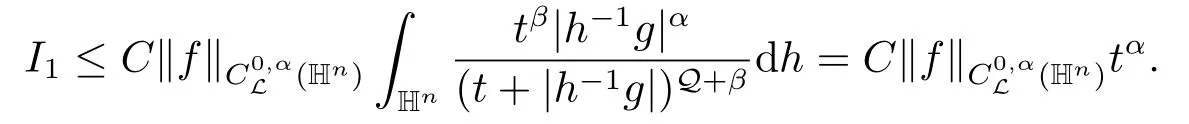
对I2,我们分两种情况讨论.当ρ(g)≤t时,由命题2.1(b),有
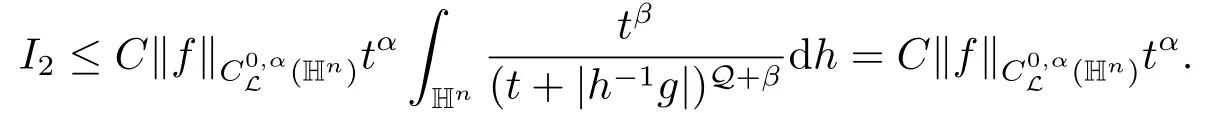
当ρ(g) >t时,因为q >Q,所以δ = 2-Q/q >1.我们取δ′使得α <δ′≤δ,δ′<β.通过命题2.1(d),可得
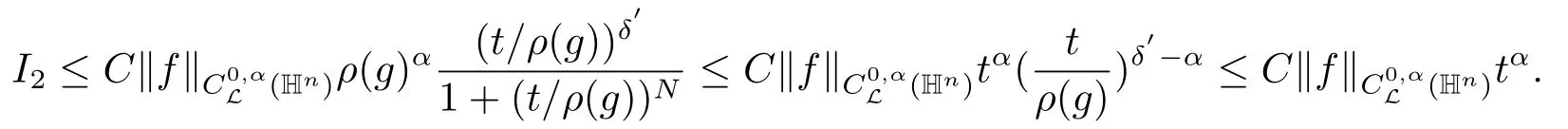
证明(iii)⇒(i).类似于文[16],利用Hardy型空间的原子分解,我们可以证明下面平方函数
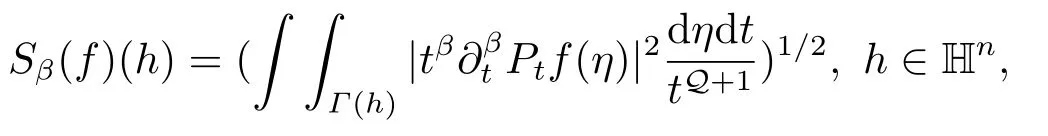
定理2.3假设q >Q,令σ是一个正数,0 <α <1,并且
(iii) 令a是一个在[0,∞)上的有界函数并且定义
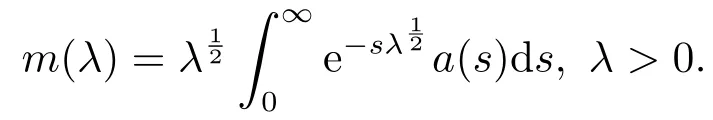
证首先证明(i).因为所以有
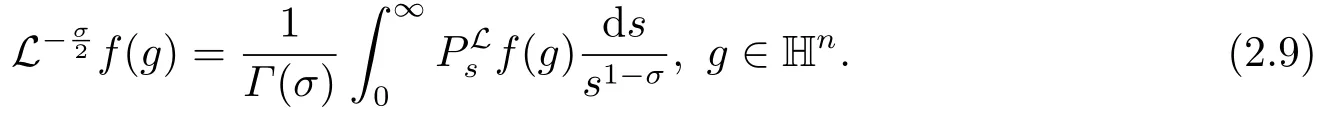
通过引理2.1(iii),由|f(g)|≤Cρ(g)α,可得
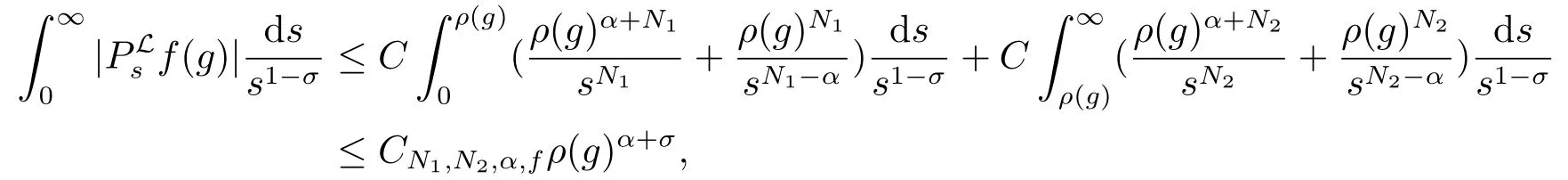
这里0 <N1<σ,并且N2>α+σ.因此,Lf(g) ≤Cρ(g)α+σ.通过引理2.1和定理2.2,对任意的β >α+σ,可以证明由(2.9)式和引理2.1,用Fubini定理,可得
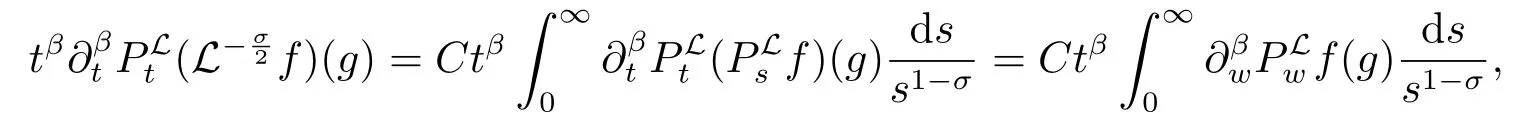
这里w =t+s.因为β >α+σ,通过定理2.2可得
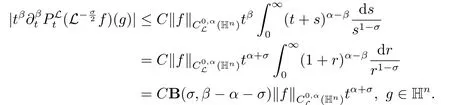
下面证明(ii).对任意的β >α,由于0 <σ <α <1,我们有
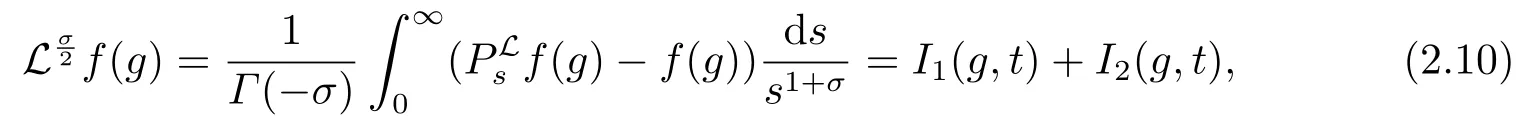
这里I1(g,t)表示从0 到t的积分.因为通过引理2.1(ii),可得
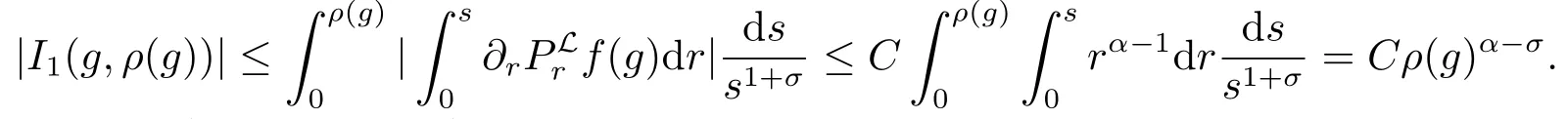
在引理2.1(iii)中,取N =α,有
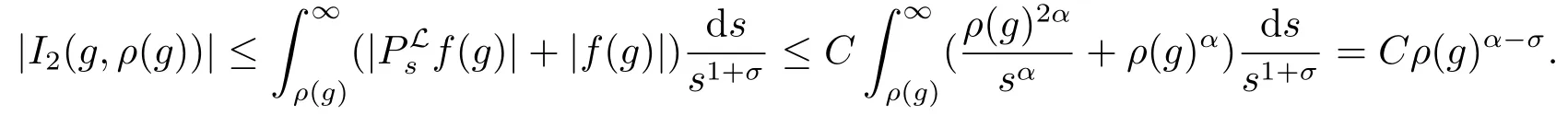
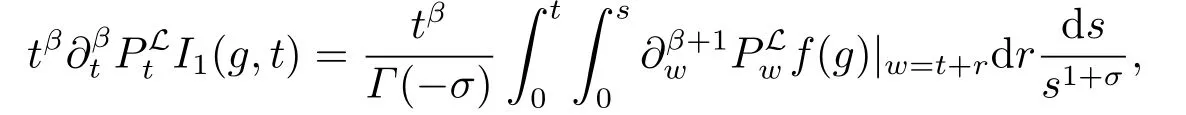
由于β >α,通过定理2.2,可得
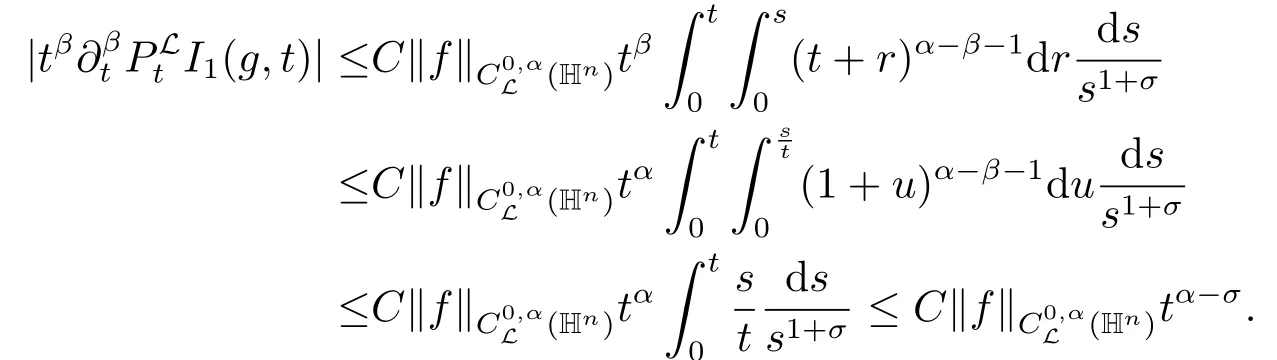
通过定理2.2和Fubini定理,可得
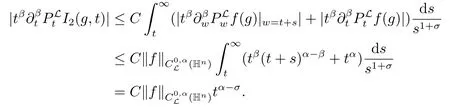
所以(ii)得证.
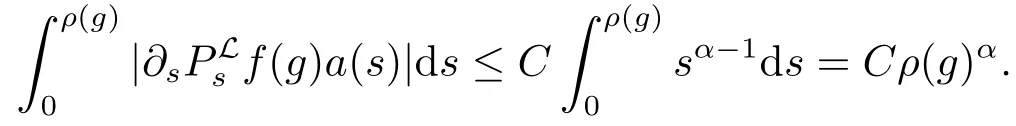
通过引理2.1(ii),β =1和N >α,可得
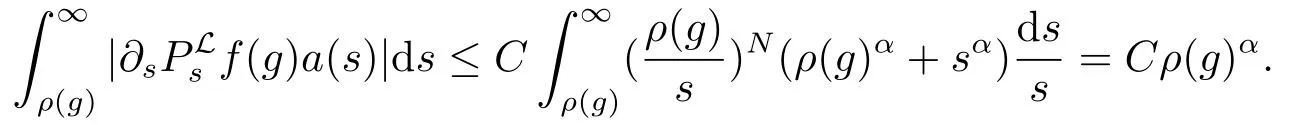
因此,|m(L)f(g)|≤Cρ(g)α.
通过定理2.2和Fubini定理,得到