黄小利,高岳林,谢金宵,谷剑峰
(1.北方民族大学数学与信息科学学院,宁夏 银川750021;2.宁夏科学计算与智能信息处理协同创新中心,宁夏 银川750021)
1.引言
本文主要考虑以下形式的二次约束二次规划问题:
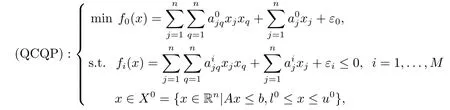
这里fi(x),i = 0,1,...,M是非凸二次函数.()n×n是n × n阶实对称矩阵,,εi∈R,i = 0,1,...,M,j = 1,...,n,q = 1,...,n,A ∈Rm×n,b ∈Rm,l0= (,...,T,u0=(,...,)T,X0为非空有界闭集,记H0= [l0,u0],H0是超矩形.非凸二次约束二次规划(QCQP)问题在实际生活中应用范围广泛[1-4],并且通常是全局优化问题,但在解决过程中往往存在许多局部最优解而不是全局最优解,且(QCQP)问题是一个NP-hard问题[5],这就使得在理论和计算方面存在巨大的挑战.因此,寻找一种有效的算法全局求解(QCQP)问题是十分有必要的.从(QCQP)问题的研究历程来看,已经有许多算法都适用于求解全局(QCQP)问题,现如今分支定界算法已成为求解该问题最常用的工具之一.根据分支定界算法的框架,基于对(QCQP)问题的松弛,在分支定界树的每个节点求解松弛子问题的下界,得到一个高质量的下界对原问题起着至关重要的作用.目前的(QCQP)松弛方法建立在多种松弛技术上,包括基于凹凸包络的线性规划松弛[6-7],拉格朗日对偶松弛[6,8],基于二阶锥规划(SOCP)的松弛[9],基于半定规划(SDP)的松弛[10].在求解盒约束非凸二次规划时,文[11]在有限分支中使用半定规划松弛技术.在求解带线性约束的非凸二次规划问题(LCQP)时,文[12]基于一阶KKT条件的有限分支和多面体半定松弛求解(LCQP).在求解带球和线性约束的非凸二次规划问题时,文[13]利用了半定规划松弛逼近非凸二次规划问题.在求解带一个非凸二次约束的二次规划问题时,文[14]将问题转化为一个无非凸约束的参数二次规划问题,通过迭代求解并在每次迭代中更新参数.在求解带多个二次约束的非凸二次规划问题时,文[15]给出了非凸二次约束二次规划(QCQP)问题的新的凸松弛方法,将每个非凸约束分解,并松弛为两个二阶锥约束,将这些非凸约束与线性约束的乘积线性化,以构造一些新的有效约束; 文[16]基于特征值分解的分支定界算法来求解(QCQP)问题,在特征值分解中,非凸分量由负特征值和相应的特征向量表示,提出了一种基于半定松弛的分支定界算法来求解(QCQP); 文[17]用一种线性化方法将初始非凸规划问题化为一系列线性松弛规划问题; 文[8]将(QCQP)问题转化为拉格朗日对偶优化问题,并在更新拉格朗日乘子的同时连续求解子问题; 文[18-20]提出了一种参数线性化方法来生成(QCQP)的参数线性松弛规划,通过对可行域和目标函数的线性松弛,将初始非凸问题化为一系列线性规划问题; 文[21]利用重构线性化技术在分支树内通过连续线性化来估计所有二次项; 文[22]基于二次约束线性规划的半定松弛,引入了一种特殊的惩罚方法,得到了所谓的条件拟凸松弛,证明了条件拟凸松弛比标准半定松弛能提供更紧的界.
非凸(QCQP)问题的困难源于二次项的非凸分量,松弛过程中只需对目标和约束函数中的二次项的非凸分量部分进行操作.本文给出了求解非凸二次约束二次规划(QCQP)问题的全局优化算法.该算法结合分支定界操作和区域缩减技术,通过对非凸二次项进行新的参数化线性松弛,使用线性松弛技术将非凸(QCQP)问题转化为线性松弛规划问题,提出的线性化技术在不增加新的变量和约束的情况下,将线性松弛规划问题嵌入到分支定界操作中.为了加快算法的收敛速度,在分支和定界过程中采用了区域缩减技术,为当前不存在全局最优解的区域提供了理论可能性,可以显著减少松弛间隙.最后,数值实验结果表明,该方法能较好地解决所有存在于全局最优解中的(QCQP)问题.
本文的组成结构如下: 第一部分提出了二次约束二次规划问题,并且概述了在不同的约束条件下求解二次规划问题的相关算法.第二部分提出了新的参数化线性松弛技术从而得到含参数的线性松弛规划问题.第三部分为了加快算法收敛速度从而提出区域缩减技术.第四部分将第二部分得到的参数化线性松弛规划,以及第三部分的区域缩减技术嵌套在分支定界框架内,得到参数化线性松弛分支定界算法以求解非凸二次约束二次规划(QCQP).第五部分通过实例证明算法的有效性和可行性.第六部分得出相关结论.
2.新的参数化线性松弛技术
为了求解原问题(QCQP),本文采用一种新的参数化线性松弛技术得到原问题和其子问题的下界函数.令H ={x=(x1,x2,...,xn)T∈Rn,l ≤x ≤u}⊆H0,其中l =(l1,...,ln)T,u=(u1,...,un)T.与文[18]类似,我们定义ρ=(ρjq)n×n是一个对称参数矩阵且ρjq∈{0,1}.对于任何的x ∈H,且j ∈{1,2,...,n},q ∈{1,2,...,n},jq,ρjq∈{0,1} 给出以下定义:

对于非凸二次函数的非线性项,接下来我们提出新的线性松弛技术,定义如下:


对于任何的x ∈H,且j ∈{1,2,...,n},q ∈{1,2,...,n},j =q,ρjj∈{0,1},
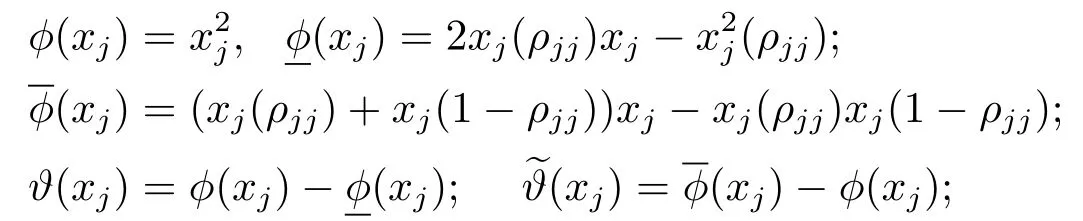
显然,xj(0)=lj,xj(1)=uj,xq(0)=lq,xq(1)=uq.
定理1对于任意的x ∈H ⊆H0,有
(a) 对任意xj∈[lj,uj],j ∈{1,2,...,n},有
(b) 对任意j ∈{1,2,...,n},q ∈{1,2,...,n},jq,有
证(a) 在每一个区间[lj,uj],j ∈{1,2,...,n}对单变量函数φ(xj) =进行线性缩放可得φ(xj)的上下界逼近函数,进而

(b) 把(xj+xq)和(xj-xq)分别看成一个单变量,则(xj+xq)2和(xj-xq)2分别是在区间[lj+lq,uj+uq]和[lj-uq,uj-lq]上关于(xj+xq)以及(xj-xq)的凸函数,则由(a)

结合式(2.1)-(2.4),




由(2.5)和(2.6)式可知,当|lj-uj|→0时,

因为
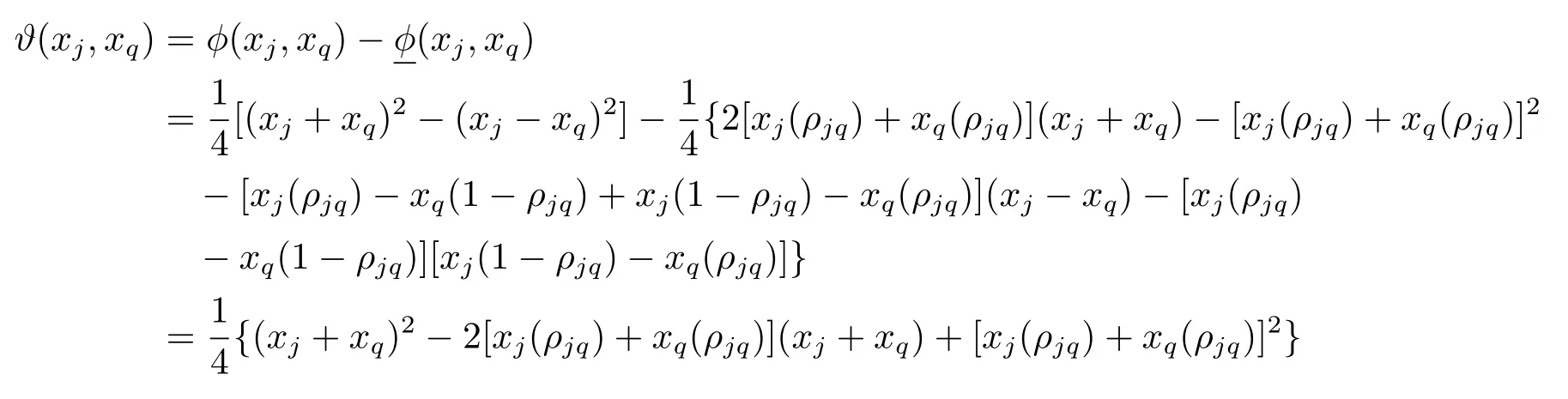
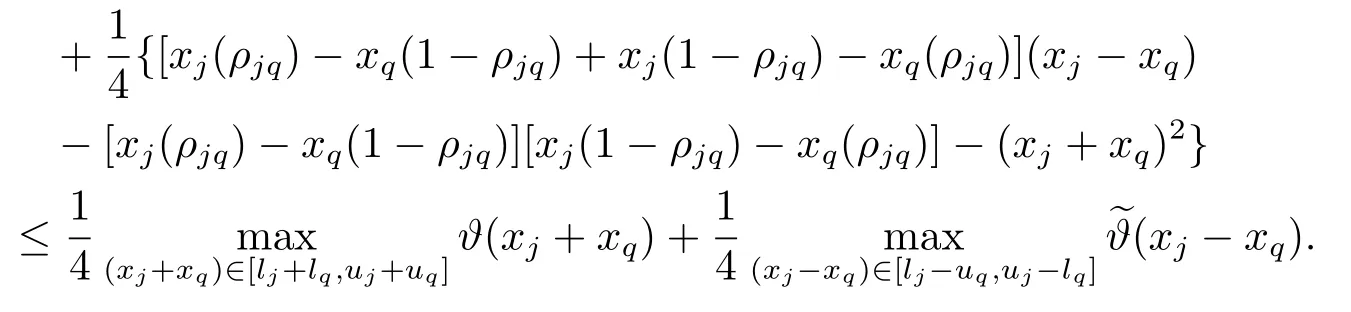
根据(2.9)及(2.12)式得,当‖l-u‖ →0时,有ϑ(xj,xq) →0.和以上证明方法类似,当‖lu‖→0时,我们可以得到证毕.
对于任意xj∈[lj,uj],j ∈{1,...,n},我们得到(x),i=0,1,...,M.即

通过以上讨论,我们得到原问题(QCQP)在子矩形H上的线性松弛规划问题如下:

定理2对于任意的x ∈H =[l,u]⊂H0,有
(a)fi(x)≥(x),i=0,1,...,M;
(b) 当‖l-u‖→0时,fi(x)-(x)→0,i=0,1,...,M.
证(a) 由(2.13)式我们很容易得到fi(x)≥(x),i=0,1,...,M;


由定理2可以知道,对每一个子矩形H来讲,线性松弛规划问题(LRP)的目标函数和约束条件函数是小于等于原问题(QCQP)的目标函数和约束条件函数的,也就是说定理2保证了问题(LRP)的最优值为原问题(QCQP)能够提供可靠的下界,当‖l-u‖ →0时,线性松弛规划问题(LRP)限逼近原问题(QCQP),这说明了算法是全局收敛的.
3.缩减技术
为了加快算法的收敛速度和计算速度,在这一部分,基于文[17-18],提出适用于本算法的区域缩减技术.当算法迭代到第k步时我们需要判断在矩形区域H上原问题(QCQP)是否存在全局最优解.此处缩减技术的前提是未删掉在矩形区域H 上原问题(QCQP)的全局最优解,进而对区域进行缩减,具体见定理3和定理4.
不失一般性,假设线性松弛规划问题LRP中的每一个线性函数φi(x),i=0,1,...,M,M+1,...,M +m,可以表示为
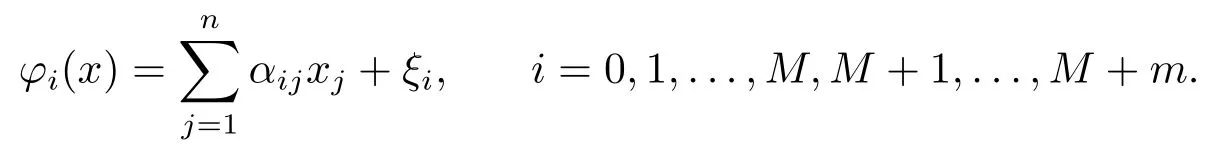
设UBk是算法迭代到第k步原问题(QCQP)当前已知的最好上界,并令

定理3对于任何的子矩形Hk⊆H ⊆H0且Hk= [lk,uk].如果存在s ∈{1,2,...,n}使得则在子矩形Hk上原问题(QCQP)没有全局最优解; 否则,如果存在s ∈{1,2,...,n}使得当且则原问题(QCQP)在子矩形上没有全局最优解; 当且则原问题(QCQP)在子矩形上没有全局最优解.其中,

证如果存在s ∈{1,2,...,n}使得则
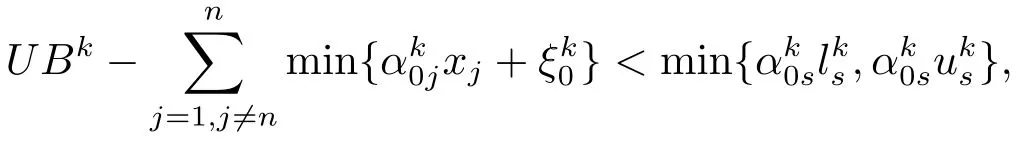
即

因此,原问题(QCQP)在Hk上没有全局最优解.接下来记x的第s个分量为xs,因为所以有当时,对于一切的x ∈Hk1,由的定义和上面的不等式,有

也就是

因此,对于任意x ∈Hk1,线性松弛函数φ0(x)要大于原问题(QCQP)的上界UBk,所以在Hk1上不存在原问题(QCQP)的全局最优解.
类似地,对于所有的x ∈Hk2,存在s ∈{1,2,...,n}使得<0且时,在Hk2这个子矩形上也不存在原问题(QCQP)的全局最优解.证毕.
定理4对于任何的子矩形Hk⊆H0且Hk= [lk,uk].如果1,...,M,M+1,...,M+m,则原问题在Hk上没有全局最优解.否则,若存在s ∈{1,2,...,n}使得且...,M,M+1,...,M+m,则原问题在子矩形Hk3上没有全局最优解; 若存在s ∈{1,2,...,n} 使得<0且则原问题在子矩形Hk4上没有全局最优解.其中,

证使用与证明定理3类似的方法,我们可以得到此定理成立.
由定理3和定理4,采用缩减技术删掉不含有原问题(QCQP)全局最优解的区域.令H =(Hj)n×1是H0任一子矩形,其中Hj=[lj,uj].得到缩减规则如下:
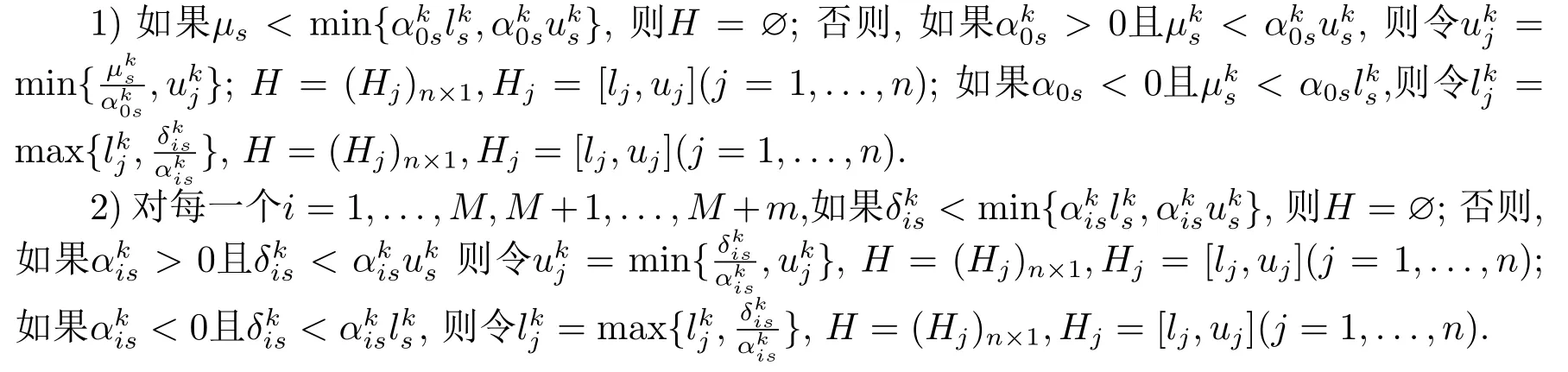
4.分支定界算法及其收敛性分析
为了得到原问题(QCQP)的全局最优解,提出了参数化线性松弛分支定界算法.在矩形H ⊆H0被剖分后的子集上求解对应的线性松弛规划问题.分支过程中,需要依据一定的剖分规则将初始超矩形H0分成两个新的子矩形.本文所采用的是标准矩形二分方法.考虑任一通过H ={x ∈Rn|lj≤xj≤uj,j =1,...,n}⊆H0所确定的子节点问题.分支规则如下所示:
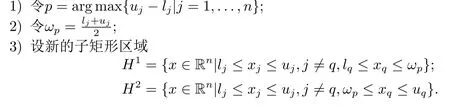
通过以上分支规则,将矩形区域H剖分成了两个子矩形H1和H2.
为了方便起见,我们把缩减后产生新的矩形区域仍然记为Hk,它是初始超矩形区域的子集.记LBk是线性松弛规划问题(LRP)在子矩形Hk上的最优值,xk= x(Hk)是相对应的最优解.结合前面所提到的线性松弛规划问题,区域缩减技术以及分支规则,为求解问题(QCQP)提出分支定界算法,步骤如下:
步0(初始化) 设置误差精度ϵ>0,初始迭代次数k =0,Q表示剪支后所有矩形的集合,初始的可行集为W =∅,初始上界UB0=+∞.
在初始矩形H0上求解线性规划问题LRP(H0),如果不可行,则原问题(QCQP)无解; 否则将求得的最优值和最优解分别记为LB0和x0.如果x0对(QCQP)可行,置可行集为W =W ∪{x0},则初始上界UB0=f0(x0),Q=Q ∪{H0},置k =1,转步1;
步1(终止准则) 如果UBk-LBk<ϵ,则迭代终止,xk是问题(QCQP)的ϵ-全局最优解.否则,转步2;
步2(矩形区域的分支) 在Q中选择出当前最小下界所对应的矩形Hk,通过本文所提出的分支规则将矩形区域Hk剖分为两个新的子矩形Hk1和Hk2,用表示新剖分的矩形集合;
步3(矩形区域的缩减) 对每一个子矩形Hkt∈,t = 0,1,2,利用本文所给出的区域缩减技术分别对子矩形进行缩减;
步4(剪支规则) 令Q=Q{Hk:LBk-UBk>ε,Hk∈Q},转步5;
步5(更新上界) 如果W = ∅,那么UBk保持不变; 如果W∅,则更新上界,UBk=min{f0(x):x ∈W},当前最好的可行点为x*:=arg minx∈Wf0(x);
步6(更新下界) 如果Q = ∅,那么LBk保持不变; 如果Q∅,那么LBk= min{LRP :Hk∈Q},置k =k+1,返回步1继续执行.
为了证明本文的分支定界算法是全局收敛的,故给出下面的定理5,以保证当‖l-u‖→0时线性松弛规划问题(LRP)地逼近于原问题(QCQP).
定理5假设(QCQP)问题的可行域是非空的,且矩形的剖分是耗尽的,则以下两个结论成立:
(a)如果算法迭代在有限步终止,则(QCQP)问题的全局最优解将在算法终止时得到;
(b)如果算法迭代在有限步不能终止,并且产生无穷多个可行点的序列{xk},则{xk}的任何一个聚点x*都是问题(QCQP)的全局最优解.
证(a)如果算法迭代在有限步终止,那么我们假设算法是在第k次迭代终止,k ≥0.根据算法的步1得到UBk-LBk≤ϵ,表示原问题(QCQP)存在可行解并设为x*,使得UBk=f0(x*),同时有

假设v是原问题(QCQP)的全局最优值,由下界的计算过程表明

因为x*是原问题(QCQP)的可行解,有

联立式(4.1)-(4.3)得

所以,x*是问题(QCQP)的ϵ-全局最优解.
(b) 如果算法的迭代是无限的,则通过求解一系列问题(LRP)可产生原问题的可行解序列{xk}∈H0.根据分支定界算法的结构,随着可行域的不断剖分加细我们有

因为下界序列{LBk=xk)}是单调不减且有上界,且上界序列{UBk= f0(xk)}是单调不增且有下界,故原问题的上下界都是收敛的.对式(4.5)两边取极限可得


不失一般性,假设超矩形序列{Hk= [lk,uk]}满足xk∈Hk以及Hk+1⊆Hk.在算法进行迭代过程中,最终矩形的剖分是耗尽的,即根据函数f0(x)的连续性,我们有

所以,序列{xk}的每一个聚点x*都是问题(QCQP)的全局最优解.
5.数值实验
给出以下几个算例证明本文算法的有效性.本文算法中所有的线性规划问题均选用对偶单纯形法求解,算法所有测试过程均用MATLAB9.2.0.538062 (R2017a)在Inter(R)Core(TM)i5-8250U,CPU@1.60GHz,8GB内存,64位Windows10操作系统的计算机上运行.
算例1[17-18]:
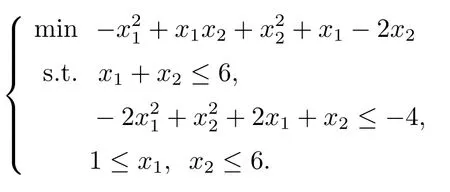
算例2[17-18]:

算例3[17-18]:

算例4[17]:

算例5[17]:

算例6[17]:

算例7[21]:

其中Q0∈Rn×n的每个元素在区间[0,1]随机产生,Qi∈Rn×n(i = 1,2,...,m)的每个元素在区间[-1,0]随机产生; d0∈Rn的每个元素在区间[0,1]随机产生; di∈Rn(i = 1,2,...,m)的每个元素在区间[-1,0]随机产生; 每一个bi∈R(i=1,2,...,m)在区间[-300,-90]产生.
算例8[17-18]:


表5.1 算例1-6利用本文算法产生的数值结果

表5.2 算例7 利用本文算法产生的数值结果
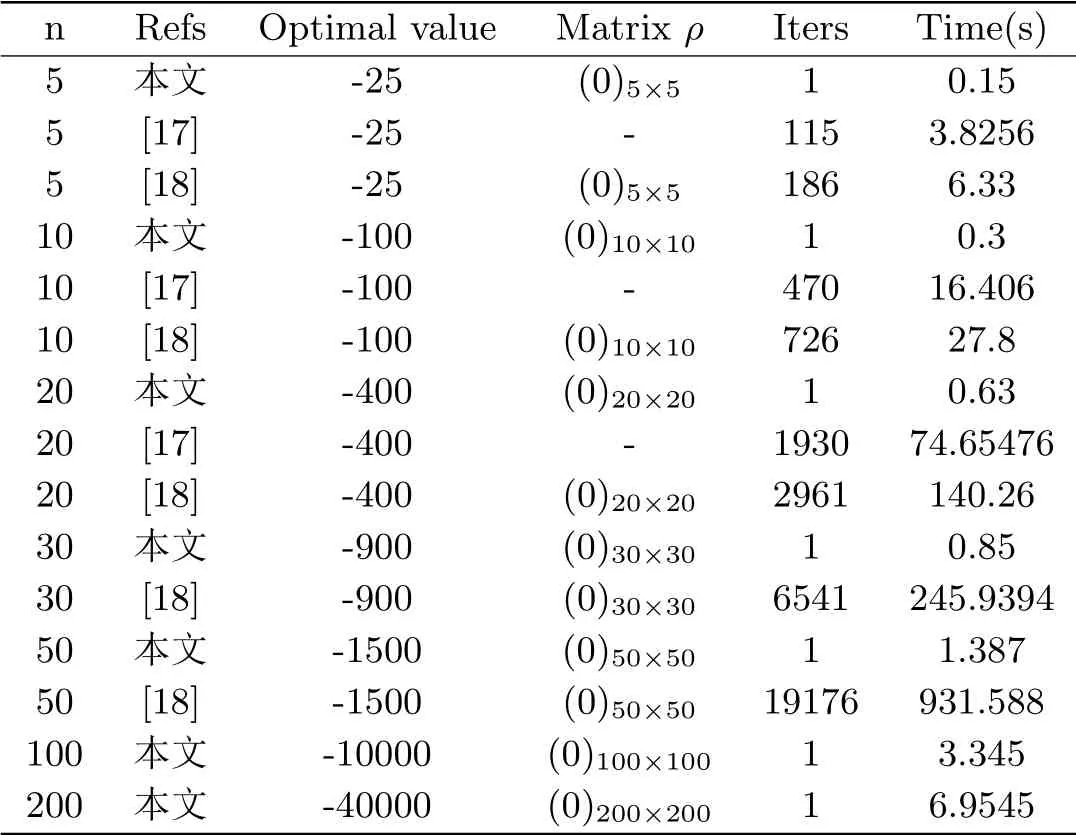
表5.3 算例8 利用本文算法产生的数值结果
为方便起见,表5.1-5.3 的具体符号表示如下: E: 算例编号; Refs: 文献; Matrix ρ: 对称参数矩阵; f0(x*): 最优值; x*: 最优解; m: 二次约束的个数; n: 目标函数的维数; Iters: 平均迭代次数; Time(s): 平均运行时间,算法运行过程中的精度为10-6.算例1-6的计算结果如表5.1所示,利用文[17-18]和本算法进行比较,从总体上看本文要优于文[17-18]的计算效果,而从算例3和算例5的结果来看,本文计算时间要比文[18]长,但比文[17]用时短,证明了我们提出的算法是可行有效的.
为了进一步证明我们的算法能够解决带有多个二次约束的二次规划问题,对算例7 进行了如表5.2 结果所示的中高维度的伪随机试验,在表5.2 中,我们把参数矩阵ρ ∈Rn×n固定成ρ = (0)n×n.当约束条件个数固定,维数逐渐增大的情况下,迭代次数没有明显的增加,且运行时间较少; 当维数固定,二次约束的个数不断增加时,迭代次数增大且运行时间越长.表5.3 中,列出了我们的算法和文[17-18]中算法的数值结果,参数矩阵ρ的元素是全为0的对称矩阵,通过比较数值结果,不管从迭代次数还是从CPU运行时间,都可以看出我们的算法是优于文[17-18]的,随着维数的增加,运行时间在增加,但迭代次数只有1次,说明本算法对算例8的维数大小不是很敏感.数值结果表明我们的算法是有效的.
6.结论
针对一般的二次约束二次规划问题,本文基于参数化方法求解关于二次项以及双变量的线性松弛问题.为了加快算法的收敛速度,利用参数化线性松弛分支定界算法,以及结合区域缩减技术,解决了二次约束二次规划问题.通过剖分矩形区域并解决参数化线性子问题,提出的算法最终收敛到原问题(QCQP)的全局最优解,在第五部分数值实验中,验证了在求解二次约束二次规划问题时本文算法是有效可行的.



