杨苗苗,葛永斌
(宁夏大学数学统计学院,宁夏银川750021)
1.引言
Helmholtz方程是一个椭圆型偏微分方程,代表了波动方程与时间无关的解.这个方程模拟了各种各样的物理现象.其中包括:振动分析、水波传播、声波散射、电磁散射、以及雷达散射等问题.随着Helmholtz方程被广泛地应用在工程和科学领域的研究中,该方程本身的复杂特性给数值计算带来了巨大困难,特别是对于变波数和大波数问题的有效数值计算,虽然其数值解法有很多,但都需要进一步提高计算精度和计算效率,以适应实际复杂大规模问题的求解.所以,对Helmholtz方程的高效精确数值求解方法的研究具有重要的理论价值和实际意义.
无网格法[1]是近年来兴起的一种新型、高效的数值计算方法.它基于点的近似思想来构造近似函数,适用于分析各类具有大梯度、奇异性等特殊性质的应用问题.目前发展的无网格方法包括无单元Galerkin法[2]和无网格配点法[3]等.对于无网格配点法,重心插值配点法就是其中的一种.重心插值配点法包括重心Lagrange插值法和重心有理插值法,是指未知函数的近似函数在插值节点处的重心型插值,是一种依赖于偏微分方程的强形式的配点法.该数值方法具有易于理解,思想结构简单,计算精度高,便于编程的优点.近年来,刘婷和马文涛[4]采用重心Lagrange插值配点法求解了二维电报方程,得到了一种高效的数值方法.王彩珍等[5]利用重心插值配点法,构造了二维非线性椭圆型方程所对应的离散方法,得到了一种计算效率更高的数值解法.
对于Helmholtz方程的求解,近年来研究者们提出了很多无网格方法,如李鹏等[6]直接利用最小二乘法建立系统的变分公式,推导了大波数Helmholtz问题的加权无网格公式.何锃等[7]通过使用加权正交基函数构造了改进的移动最小二乘法,并结合拉格朗日乘子法离散Dirichlet边界条件,推导了求解该方程的无网格加权最小二乘法.陈黄鑫和邱伟峰[8]提出了一种求解大波数Helmholtz方程的一阶系统最小二乘法,并利用一个非平凡分解来解决对偶的一阶系统最小二乘法问题.杨子乐等[9]利用无网格节点MIP法的d适应性和移动最小二乘法来构造近似函数,给出了求解Helmholtz方程的两种计算方法.李莹等[10]采用无网格局部径向基点插值法,将径向基函数耦合多项式基函数作为近似函数,克服了无网格法中场函数在计算中的冗余性.Assari等[11]将局部支撑薄板样条的离散配点法近似化为一类具有自由形状参数的径向基函数法,用一种特殊的非等距Gauss Legendre求积法来计算出现的对数型奇异积分,发展了一种求解具有对数积分方程的无网格法.李美香等[12]将三角函数作为基函数,并在局部支持域内构造了一种形函数,研究了带有边界层问题和波传播问题的Helmholtz方程.张伟和丁睿[13]通过引入全局径向基函数和正定紧支径向基函数构造了求解Helmholtz方程的Galerkin型的无网格方法,使得求解方法有效且具有高精度.屈文镇等[14]发展了一种新的局部基本解方法,与传统的基本解法相比,该方法根据节点将计算域划分为若干重叠子域后得到了稀疏的带状矩阵,可以求解大波数Helmholtz问题.陈林冲和李小林[15]基于无网格和无边界分析,利用Burton-Miller公式提出了一种无边界方法,该无网格方法对所有的波数都能求出唯一解,并且只涉及到边界节点,还可以处理特大波数下的Helmholtz问题.
本文针对如下一维Helmholtz方程:
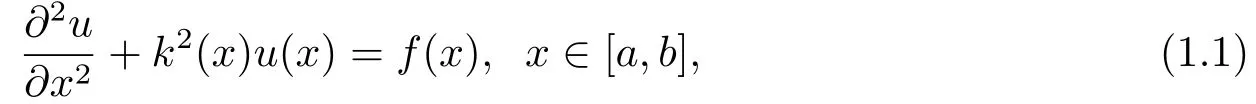
其中[a,b]是求解域,u(x)是关于x的未知函数.k(x)表示波数,可以是常数,也可以是关于x的函数.f(x)是源项.定义Dirichlet边界条件为

借助Chebyshev插值节点和三种测试节点,运用重心Lagrange插值基函数和重心有理插值基函数推导了求解该类方程的两种无网格配点法.该重心插值方法理论简单,需要的插值节点少,最后得到的离散矩阵处理方便,不仅可以计算大波数问题,还可以计算变波数问题.具有推导过程简单,计算结果精度高和稳定性好等的优点.主要内容如下:第二节推导一维重心Lagrange插值和重心有理插值的计算公式和一些简化矩阵的理论知识.第三节推导计算一维Helmholtz方程的两种插值配点法及其离散矩阵.第四节给出一些测试问题的计算结果,并与一些文[19-21]中结果进行对比,最后给出本文的结论.
2.重心插值公式
在区间[a,b]上插入n+1个节点xi,则有a=x0<x1<x2<···<xn=b,设未知函数u(x)在节点处的函数值ui=u(xi),i=0,1,···,n,则Lagrange多项式插值公式可表示为:

其中Li(x)为Lagrange插值基函数,具体形式为:

令

定义重心Lagrange插值函数的权重为:

此时,插值基函数(2.2)式可变为:
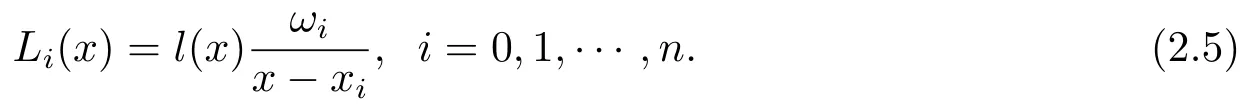
将(2.5)代入(2.1)式,得:

则上式被称作改进的Lagrange插值公式.相比Lagrange插值公式,上式在插值节点的数目增加时,计算量减少很多,由O(n2)变为O(n).
利用(2.6)式插值常数1,即给定一组节点为(xi,1),i=0,1,···,n,得:.
化简后可得:

将(2.7)代入(2.6)式中可得:

则上式被称为重心Lagrange插值公式[16],相比式(2.6),式(2.8)在保持相同计算量O(n)的同时,还能有效地克服Runge现象.
重心有理插值和重心Lagrange插值相类似,重心有理插值即是将Lagrange函数换为有理函数进行插值.下面我们构造重心有理插值基函数.
首先,选择一个正整数d,且0≤d≤n.对于节点xi,i=0,1,···,n-d,选择d+1个节点(xi,ui),(xi+1,ui+1),···,(xi+d,ui+d)后,我们利用重心Lagrange插值多项式的形式,构造

然后,根据pi(x)构造一个权函数

最后,利用pi(x)和λi(x)构造出重心有理插值函数
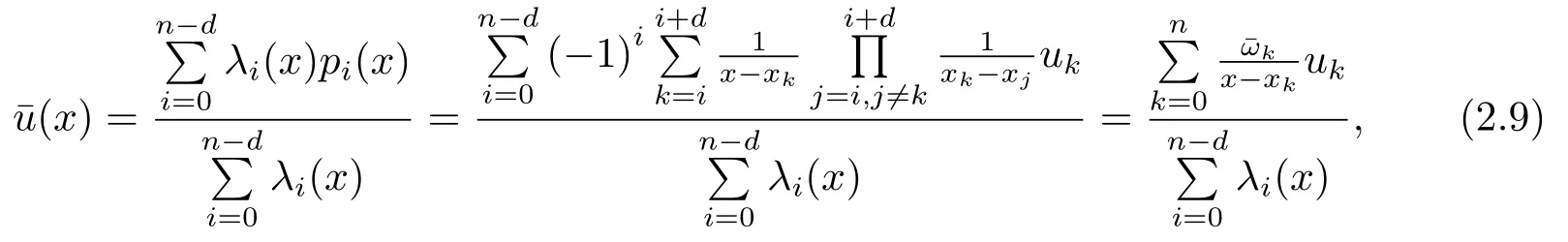

利用常数1的Lagrange插值公式,有

由此可得

将(2.11)代入(2.9)中可得重心有理插值公式:


则上式被称为重心有理插值公式[17].需要说明的一点是,文[17]中已经证明式(2.13)构造的有理插值的误差阶为O(hd+1).其中h是等距节点网格步长.因此只要选择合适的参数d,式(2.13)就可达到更高的插值精度,从而得到更小的误差.
从重心Lagrange插值权函数的表达式(2.4)和重心有理插值权函数的表达式(2.10)能够看出,插值权的选取跟节点的分布有关.因此我们考虑了三种不同的节点来进行函数插值和数据测试,它们分别是随机节点、等距节点和Chebyshev节点.由于在进行具体的程序计算时,随机节点和等距节点可直接调用命令,因此,这部分只给出Chebyshev节点的计算公式:
第一类Chebyshev节点:(Chebyshev I)
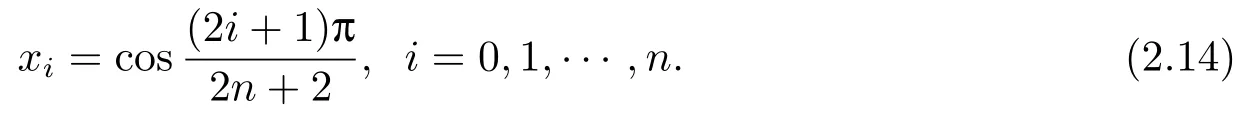
第二类Chebyshev节点:(Chebyshev II)

需要说明的是,对于两类Chebyshev节点的公式,其定义区间为[-1,1],当针对一般的区间[a,b]时,利用区间的坐标变换公式进行转化即可.
微分矩阵最初是在研究Chebyshev拟谱方法[18]时提出的,重心插值微分矩阵能够直接获得Helmholtz方程中未知函数在计算节点处的导函数,因此,微分矩阵是重心插值配点法求解里非常重要的一部分.
由式(2.8),函数的重心Lagrange插值公式可表示为:


通过对比我们可以看出,两种重心插值公式的根本区别是权函数的不同.不难发现,重心有理插值除了必要的计算外,还需选取参数d.除此之外,两种重心插值法在形式上是一致的.因此,利用(2.16)和(2.17)式,函数在节点xj(j=1,2,···,n)处的m阶导数可以分别表示为:

写成矩阵的形式为


3.Helmholtz方程的离散
方法I重心Lagrange插值方法
将重心Lagrange插值公式(2.16)代入到式(1.1)中,可得:

设xj,j=1,2,···,n,为给定的插值节点,令上式方程在所有xj上都成立,则有

注意到Li(xj)=δij,利用重心插值微分矩阵,则方程(3.2)可写为矩阵形式:

进一步可写为:

将式(2.16)代入到式(1.2)中,可得:

其中,分别表示n阶单位矩阵的第一行和第n行,g1,g2分别为具体的值.联立求解方程(3.4)和(3.5),即可求得在重心Lagrange插值公式下插值节点上的函数值ui,回代入式(2.16)中并利用测试节点进行计算可得本文方法I的数值解u(x).
方法II重心有理插值方法
同理,将重心有理插值公式(2.17)代入到式(1.1)中,可得:


4.数值算例
在本节中,我们将两种重心插值配点法应用于几个测试问题中以证明本文方法的有效性和准确性.我们给出了包括大波数和变波数Helmholtz方程的数值算例,采用本文方法进行计算并与文[19-21]中所得的数值结果进行比较.其中L∞范数误差的定义如下给出:

上式中ui和uei分别代表数值解和精确解.Nt是检测点个数.
问题1[19-20]:
考虑如下非齐次大波数Helmholtz方程

其中边界条件为:

该问题的精确解为:

首先,由于方法II在进行计算中需要优先选择参数d,并且0≤d≤N.其中N是插值点个数.因此表1给出当Nt=30,k=10时不同d和N下问题1中方法II的L∞范数误差.其中Nt是检测点个数,并且插值节点的类型为第二类切比雪夫点(Chebyshev II),测试节点也为第二类切比雪夫点.由数值结果我们可以看出,随着插值点数N的增大,当d越接近于N,方法II的计算结果精度越高,误差越小.因此在本文剩余算例关于方法II的计算中,我们统一选取d=N-1.这样既保证了方法II具有更高的精度,又得到了更小的计算误差.

表1 当Nt=30,k=10时不同d和N下问题1中本文方法II的L∞范数误差
其次,表2给出了当Nt=N,k=10时四种插值节点下问题1的L∞范数误差.由数值结果可以得出对于四种插值节点:随机节点、等距节点、Chebyshev I和Chebyshev II节点来说,随机插值节点的数值结果很差;等距节点的结果一般;Chebyshev I节点的结果远不如Chebyshev II节点,并且Chebyshev II节点的精度最高、稳定性最好、计算误差最小.因此对于插值节点的选择,我们对于本文剩余算例中的表格和图都默认选择Chebyshev II节点,简记为Chebyshev节点.此外对于两种插值方法:重心Lagrange插值法和重心有理插值法来说,所得的计算结果相差不大,即精度一样,稳定性一样,误差量级一样并且L∞范数误差也近似相等.
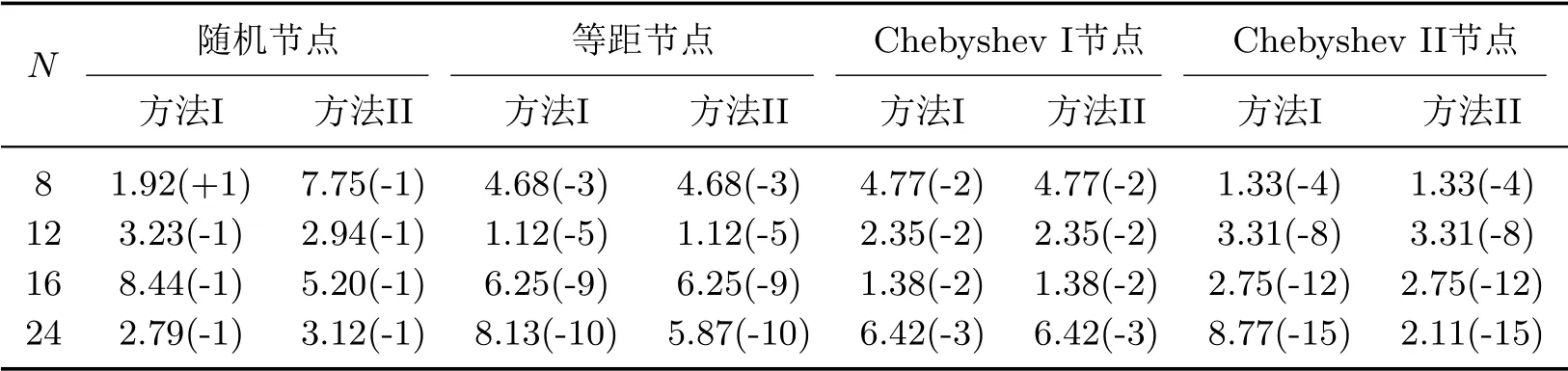
表2 当Nt=N,k=10时四种插值节点下问题1的范数误差
然后,表3给出了当Nt=50,k=10时三种测试节点下的L∞范数误差.由数值结果我们可以得出对于三种测试节点:随机节点、等距节点和Chebyshev节点来说,所得的误差量级一样,并且误差也相差不大.此外对于两种插值方法来说,所得的计算结果也相差不大.

表3 当Nt=50,k=10时三种测试节点下问题1的L∞范数误差
接着,表4给出了当N=24,k=10时三种测试节点下的L∞范数误差.由数值结果我们可以得出两种重心插值方法随着检测点数Nt的变化,所得的误差量级不变,并且L∞范数误差也相差不大.也就是说检测点的个数对于本文所提方法的误差影响不大,因此在剩余算例的计算中,我们可以取任意合理的检测点个数.

表4 当N=24,k=10时三种测试节点下问题1的L∞范数误差
最后,表5给出了当Nt=200,k=1时本文两种无网格配点法与文[19]和文[20]中方法计算L∞范数误差的比较.结果表明当N=20时,本文所提两种方法的误差量级均为O(10-15),而文[19-20]中的误差量级仅仅只达到O(10-5).而当N=160时本文所提方法的误差量级均为O(10-13),而文[19-20]中的误差量级分别为O(10-8)和O(10-12).另外,需要说明是,尽管本文所提方法的计算精度会随着插值点数N的增加而减小,但本文方法的误差量级仍然要高于文[19-20]中所提方法.此外,与有限差分法相比,无网格重心插值配点法并不意味着插值节点数越多,所得的计算结果会越好,有时候我们仅仅可能只用很少的插值节点便可得到更好的数值结果.表6给出了当Nt=200,k=1000时本文两种无网格配点法与文[20]中方法L∞范数误差的比较.结果表明本文所提两种无网格方法的计算结果要远远优于文[20]中所提方法.因此本文方法更适合求解大波数的Helmholtz问题.

表5 当Nt=200,k=1时三种测试节点下问题1的L∞范数误差

表6 当Nt=200,k=1000时不同测试节点下问题1的L∞范数误差
问题1在Nt=24,Nt=N,k=10时随机点(a),等距点(b),Chebyshev I点(c)及Chebyshev II点(d)的四种插值节点图可参见图1.由图可得:随机点不规则的分布在区间内,等距点均匀分布在区间内,两类Chebyshev点在端点处分布点数较多,中间分布点数相对较少.随后,在Nt=200,k=1000,N=160时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图参见图2.由图可得三种测试点下的精确解和数值解吻合的很好.

图1 问题1在N=24,Nt=N,k=10时随机点(a),等距点(b),Chebyshev I点(c)及Chebyshev II点(d)的插值节点图

图2 问题1在Nt=200,k=1000,N=160时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图
问题2[20]:
考虑如下非齐次变波数Helmholtz方程

其中边界条件为:

该问题的精确解为:

表7给出了当Nt=100,k(x)=时本文两种无网格配点法与文[20]中方法L∞范数误差的比较.结果表明当N=8时本文所提两种方法的误差量级均为O(10-6),而文[20]中的误差量级为O(10-4).而当N=64时本文所提方法的误差量级为O(10-14)或O(10-15),而文[20]中的误差量级为O(10-10).表8给出了当Nt=200,k(x)=时本文两种无网格配点法与文[20]中方法L∞范数误差的比较.结果表明本文所提两种无网格方法的计算结果要优于文[20]中所提方法.因此本文方法更适合求解变波数的Helmholtz问题.
表7 当Nt=100,k(x)=时不同测试节点下问题2的L∞范数误差

表7 当Nt=100,k(x)=时不同测试节点下问题2的L∞范数误差
N文[20]随机节点等距节点Chebyshev节点方法I方法II方法I方法II方法I方法II 81.610(-4)1.175(-6)1.195(-6)1.194(-6)1.194(-6)1.198(-6)1.198(-6)161.695(-6)2.887(-15)3.997(-15)2.887(-15)3.997(-15)2.776(-15)3.997(-15)321.335(-8)6.772(-15)4.996(-15)6.772(-15)4.996(-15)6.772(-15)4.996(-15)64 1.011(-10)4.219(-14)8.573(-15)4.208(-14)8.704(-15)4.186(-14)8.704(-15)
表8 当Nt=200,k(x)=时不同测试节点下问题2的L∞范数误差

表8 当Nt=200,k(x)=时不同测试节点下问题2的L∞范数误差
N文[20]随机节点等距节点Chebyshev节点方法I方法II方法I方法II方法I方法II 85.563(-4)2.046(-6)2.047(-6)2.048(-6)2.048(-6)2.048(-6)2.048(-6)166.045(-6)1.221(-14)1.366(-14)1.221(-14)1.399(-14)1.221(-14)1.399(-14)324.377(-8)2.676(-14)7.105(-15)2.676(-14)7.105(-15)2.676(-14)7.105(-15)64 3.028(-10)5.596(-14)1.993(-13)5.584(-14)1.993(-13)5.584(-14)1.988(-13)
问题2在Nt=200,k(x)=N=64时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图参见图3.由图可得三种测试点下的精确解和数值解吻合得非常好.

图3 问题2在Nt=200,k(x)==64时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图
问题3[21]:
考虑如下齐次Helmholtz方程

其中边界条件为:

该问题的精确解为:

表9给出了当Nt=100,b=0.64时不同测试节点及不同波数k=0.5N下本文两种无网格配点法的L∞范数误差.需要说明的是,文[21]中只给出了一些数值解和精确解的吻合图而没有给出相应的数据,因此表9只给了本文所提两种无网格配点法的计算结果而没有和文[21]的对比数据.计算结果表明,即使k随着N的变化而变化,但是本文的两种无网格配点法仍然精度很高,并且误差值很小,也就是说本文重心无网格方法更逼近于精确解.

表9 当Nt=100,b=0.64时不同测试节点及不同波数k=0.5N下问题3的L∞范数误差
问题3在N=40,k=0.5N,Nt=100,b=0.64时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图参见图4.由图可得三种测试点下的精确解和数值解吻合的非常好.

图4 问题3在N=40,k=0.5N,Nt=100,b=0.64时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图
问题4:
考虑如下齐次Helmholtz方程

其中边界条件为:

该问题的精确解为:
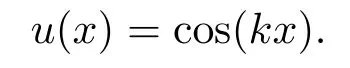
表10给出了当Nt=100,k=24时不同测试节点下本文两种无网格配点法的L∞范数误差.由数值结果可以看出,该区间上本文所提两种无网格方法的误差量级最高为O(10-6),尽管误差量级与前面几个算例比起来不高,但是稳定性仍然很好.

表10 当Nt=100,k=24时不同测试节点下问题4的L∞范数误差
问题4在Nt=100,k=24,N=56时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图参见图5.由图可得三种测试点下的精确解和数值解吻合的非常好.


图5 问题4在Nt=100,k=24,N=56时方法I与方法II在随机点(a),等距点(b)和Chebyshev测试点(c)下精确解与数值解图
5.结论
可以得出以下结论:
1)两种重心插值配点法的计算精度相同,误差也几乎相同,因此对于一维Helmholtz方程来说,两种方法的结果相差不大.
2)在插值节点的选取上,数值结果表明:随机节点很差,等距节点一般,两种Chebyshev节点结果很好,并且Chebyshev II要优于Chebyshev I.在测试节点的选取上,三种测试节点的数值结果几乎没有差异.此外,随着测试节点数量的变化,本文方法的误差几乎没有变化.也就是说,测试节点的数量对我们的数值结果影响不大.
3)与文[19-21]中所提方法相比,本文所提两种无网格配点法使用较少的节点即可获得高精度的数值结果,并保持良好的稳定性.并且数值实验研究结果进一步表明,本文方法具有所需配点数少、精度高、误差小和效率高等优点.此外,本文方法不仅可以计算大波数问题,还可以计算变波数问题,并且其数值结果要优于文[19-21]中方法结果.
4)该重心插值方法可推广到二维和三维Helmholtz方程的求解中.现正在进行此项研究.



