“圆”中的最值问题探究

高灵敏

“圆”中的最值问题探究

高灵敏

圆作为最美的几何图形，拥有很多美好的性质，作为中考试题的载体，它可以和很多知识点融合，展示各式各样的问题.圆中的最值问题便是其中一类.请同学们欣赏几例.

例1（2016·黑龙江）如图1，MN是⊙O的直径，MN=4，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为.

图1

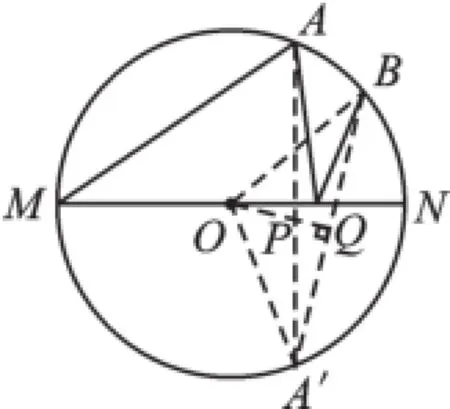
图2

【分析】过A作关于直线MN的对称点A′，连接A′B，由轴对称的性质可知A′B即为PA+ PB的最小值，由对称的性质可知再由圆周角定理可求出∠A′ON的度数，再由勾股定理即可求解.

解：过A作关于直线MN的对称点A′，连接A′B，OB，OA′，AA′，

∵∠AMN=40°，∠A′ON=80°，∠BON=40°，

∴∠A′OB=120°，

过O作OQ⊥A′B于Q，在Rt△A′OQ中，OA′=2，∴A′B=2A′Q=2·2·sin60°=2 3，

即PA+PB的最小值为2 3.

【点评】利用轴对称性质是解本题的关键.

A.8B.12C.10.5D.8.5

图3

图4

【分析】直线与x轴、y轴的交点A、B坐标可求，AB的长是定值，C（0，1）是定点，作CE⊥AB，所以当P在EC的延长线与圆C的交点位置Q处时，△PAB面积有最大值.

解：连接CA，过点C作CE⊥AB，EC的延长线交⊙C于Q，如图4.A（4，0）、B（0，-3），

∴AB=5，S△CAB=S△OAB+S△CAO=6+2=8=

例3如图5，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点.若⊙O的半径为7，则GE+FH的最大值为.

【分析】要求GE+FH的最大值，而GE+FH= GH-EF，EF作为△CAB的中位线，始终等于，是个定值，那就需要GH最大.

图5

图6

解：如图6，当GH为⊙O的直径时，GH有最大值.此时，E点与O点重合，即AC也是直径，AC=14.∴∠ABC=90°，

∵点E、F分别为AC、BC的中点，

∴GE+FH=GH-EF=14-3.5=10.5.

【点评】确定GH的位置是解题的关键，勿忘圆中最长的弦是直径这一基本事实.

例4如图7，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y= kx-3k+4与⊙O交于B、C两点，则弦BC的长的最小值为（）.

A.22B.24C.10 5D.12 3

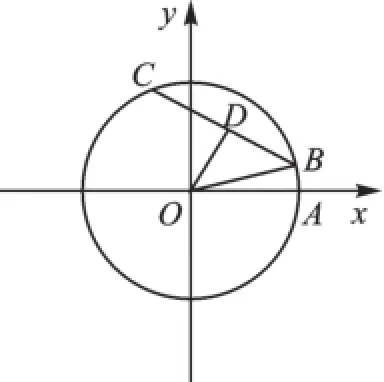
图7

【分析】直线y=kx-3k+4必过定点（3，4），记为点D.最短弦CB即为过点D且与OD垂直的弦，再求出OD=5，便可求出BC的值.

解：y=kx-3k+4=k（x-3）+4，当x=3时，y=4，故直线y=kx-3k+4一定经过点（3，4），记为点D.

∴OD=5，OB=OA=13.

由于过圆内定点D的所有弦中，与OD垂直的弦最短，∴BC的最小值为

【点评】该题的难点是确定定点（3，4），从函数关系式的特点可发现随着k值的变化，直线在不停变化，从而与圆的交点B、C也在不停改变，有没有一个点可以不受k的影响？所以将y=kx-3k+4=k（x-3）+4这样整理后，令k的系数x-3=0，y将不受k的影响.此时确定定点（3，4）.在圆内过一定点的最长弦是直径，最短弦是过该点与直径垂直的弦.

例5如图8，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，AB=8，求PM的最大值是.

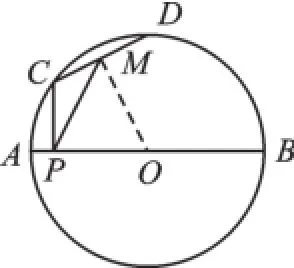
图8

【分析】见弦的中点连圆心得垂直，在四边形中见对角都是直角，得出四边形的四个顶点在同一个圆上，且直角所对的弦是直径.

解：连接OM，∵M为弦CD的中点，∴OM⊥CD，∵∠OPC=∠OMC=90°，∴O、P、M、C四点共圆.

∴当PM=OC为直径时，PM最大，最大值为4.

【点评】本题考查了垂径定理，三线合一，四点共圆，直径是最长的弦，两点之间线段最短，关键是找出符合条件的CD的位置，题目灵活，有一定的难度.

（作者单位：江苏省丰县初级中学）