吴玲芳
我们学习了与圆有关的一些概念以及圆的性质,并运用这些知识解决问题,在此过程中,容易混淆一些概念和知识点,在解题时也较容易出错。我们要理解它们的本质,并理清部分知识之间的区别和联系,为正确解答、灵活运用做好准备。
一、易混概念剖析
1.圆的定义。
圆的描述性定义:在平面内,把线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆。“在平面内”不能漏,否则,旋转1周后的图形不一定是圆。
2.同圆、等圆与同心圆。
同圆指的是同一个圆,而等圆、同心圆都是指两个圆。等圆是指半径相等、圆心不同的两个圆;同心圆指的是圆心相同、半径不同的两个圆。
3.等弧与同弧。
等弧指的是能够重合的弧,同弧指的是同一条弧。等弧只能出现在同圆或等圆中,它们所对的圆心角的度数相等,并且弧长也相等。
4.弦与弧。
连接圆上任意两点的线段叫做弦,弦是直的。圆上任意两点之间的部分叫做圆弧,简称弧,弧是圆的一部分,是曲线。
5.等圆与等弧。
它们的共同特征是“能够互相重合”,它们都是指两个图形。圆是封闭的曲线,弧是圆的一部分。
6.直径与弦。
直径是经过圆心的弦,是特殊的弦,是圆中最长的弦。但弦不一定是直径。
7.优弧、劣弧与半圆。
圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,所以半圆是特殊的弧。大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧。优弧用三个字母表示,例如︵CED。劣弧用两个字母表示,例如︵BC。半圆既不是优弧,也不是劣弧。
8.圆心与圆周角。
顶点在圆心的角叫做圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角。二者的差别:圆周角必须满足两个条件,仅有“顶点在圆上”,不能构成圆周角。
9.外接圆、内切圆、内接三角形与外切三角形。
“接”说明圆经过三角形的三个顶点,“切”说明圆与三角形的各边相切。“内”和“外”是相对的,以一个图形为标准,说明另一个图形在它的里面或外面。“圆的内接三角形”是以圆为标准,三角形在它的里面;“三角形的外接圆”是以三角形为标准,圆在它的外面;“三角形的内切圆”是以三角形为标准,圆在它的里面;“圆的外切三角形”是以圆为标准,三角形在它的外面。
10.内心、外心与重心。
三角形的内心是内切圆的圆心,是三边垂直平分线的交点,到三个顶点的距离相等。三角形的外心是外接圆的圆心,是三角形角平分线的交点,到三边的距离相等。三角形的重心是三条中线的交点,把每一条中线分成2∶1的两部分。
11.切线与切线长。
切线是一条直线,与已知圆只有一个公共点。切线长指的是切线上的一条特殊线段的长度:在经过圆外一点的切线上,该点与切点之间的线段的长,叫做该点到圆的切线的长。如图1,直线PA和直线PB是⊙O的切线,PA=PB,这两条线段的长就是P点到⊙O的切线长。
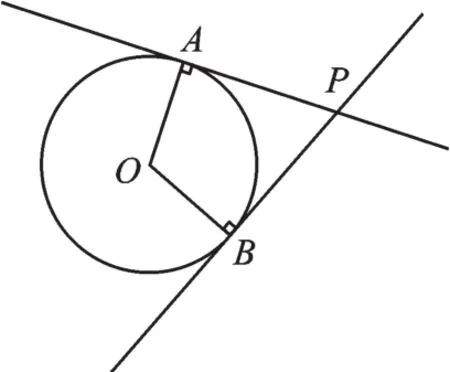
图1
12.正多边形、中心与半径。
各边相等、各角也相等的多边形叫做正多边形。仅有各边相等或各角相等,不能判别正多边形。例如,矩形的各角相等,由于各边不一定相等,所以不是正四边形;菱形的各边相等,但因为各角不一定相等,所以不是正四边形。正多边形的外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径。不仅圆有半径,正多边形也有半径。
二、易错点剖析
1.圆的对称性。
在同圆或等圆中,如果两个圆心角、两条弦、两条弧中有一组量相等,那么这组量所对应的其余各组量都分别相等。这里一定要有前提“同圆或等圆”,否则结论不一定成立。例如,图2中,在两个同心圆中,AB=EF,但是弧AB≠弧EF,∠AOB≠∠EOF;在这两个同心圆中,∠DOC=∠GOH,但是 CD≠GH,弧 CD≠弧GH。已知两条弧相等,则其他两组量一定相等,因为等弧只能出现在同圆或等圆中。
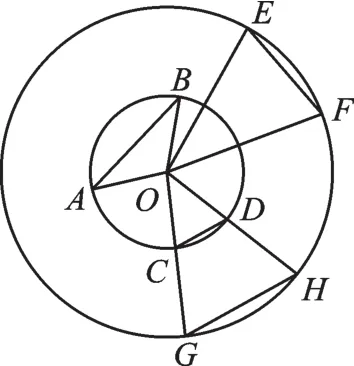
图2
2.垂径定理。
垂直于弦的直径平分弦,并且平分弦所对的两条弧。但是若一条弦被直径平分,那么它与直径不一定垂直。从一般情形来看,如图3,当弦CD被直径AB平分时,可利用OD=OC,根据等腰三角形的三线合一,推得弦CD与直径AB垂直。但是在特殊情形下(图4),这条弦CD是特殊的弦——直径时,由于任意两条直径一定互相平分,所以,它们不一定垂直。
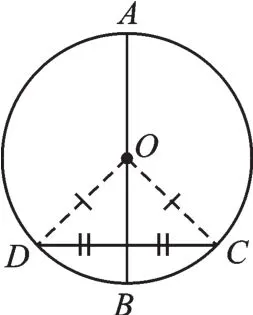
图3
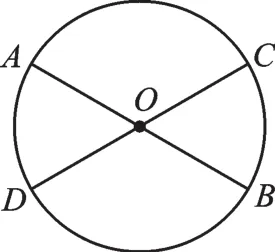
3.确定圆的条件。
过一点有无数个圆;经过两点有无数个圆,圆心在两点连线的垂直平分线上;不共线的三点确定一个圆,前提是“三点不在同一条直线上”。
4.圆周角定理。
同弧或等弧所对的圆周角相等。该定理的逆命题是:如果在同圆或等圆中,两个圆周角相等,那么这两个圆周角所对的弧也相等或相同。该逆命题是真命题,但是不能直接运用。在解题时,可以通过圆心角转化,或者先说明圆周角的度数是所对弧的度数的一半。
例1 在⊙O中,A、B、C、D都在圆上,已知AC平分∠BAD,求证BC=DC。
【解析】本题考查圆周角定理、圆的对称性。
法一:如图5,因为AC平分∠BAD,所以∠1=∠2。由于“圆周角的度数等于它所对弧上的圆心角度数的一半”,而圆心角的度数等于它所对弧的度数,所以圆周角的度数是所对弧的度数的一半。可知︵
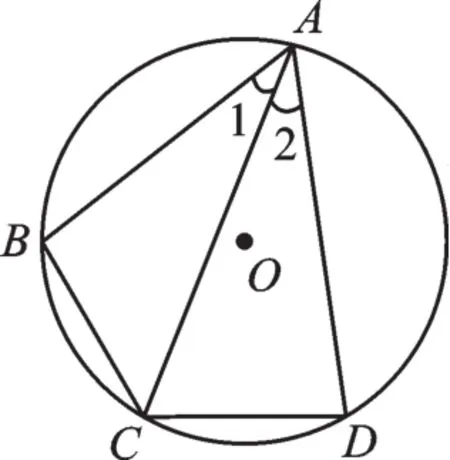
图5
法二:如图6,连接OB、OC、OD,利用圆周角定理,圆周角的度数等于它所对弧上的圆心角度数的一半,可得∠BOC=2∠1,∠COD=2∠2,所以∠BOC=∠COD,根据圆的对称性,BC=DC。
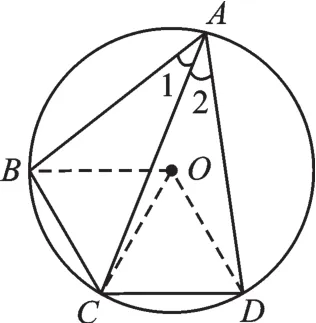
图6
【点评】由于圆周角定理︵没有︵逆定理,所以根据∠1=∠2,不能直接得到BC=CD,需要通过“圆周角的度数等于它所对弧上的圆心角度数的一半”来转化,或者利用辅助线,通过圆周角定理、等量代换等来证明结论。
5.扇形的弧长与面积公式。
扇形为l)。第二种方法类似于三角形的面积公式,把扇形的弧长看成“底”,扇形的半径看成“高”,S=×底×高,这样也便于记忆。扇形扇形的弧长与面积公式较为相似,容易混淆。我们并不需要死记硬背,可以利用扇形和圆的关系来推导。若有半径相同的扇形与圆,则扇形的弧长是圆的周长的,扇形的面积是圆的面积的。
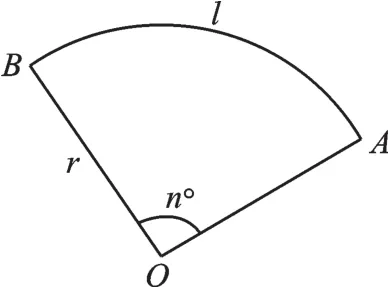
图7
6.圆锥与扇形。
将圆锥沿一条母线剪开,圆锥的侧面展开图是一个扇形。展开后的扇形半径R是圆锥的母线l母线,扇形的弧长l弧长是圆锥底面圆的周长。为了避免混淆,我们在列出公式时,可以在相应的字母下面标注下标。S侧面积=πr底l母线,在具体的问题中还要挖掘已知条件中的隐含信息。
例2 一个圆锥的侧面展开图是一个半径为R的半圆,那么圆锥的底面圆的半径是。
【解析】半圆的半径R是圆锥的母线l母线,半圆的弧长l弧长=圆锥底面圆的周长。设圆锥底面圆的半径为r,由题意可知,所以R=2r
【点评】本题主要根据圆锥侧面展开图与圆锥底面圆的关系解答,需要弄清两个半径的不同意义。这里还有个隐含的信息,就是半圆是特殊的扇形,圆心角为180度。
7.外心的位置。
内心只能在三角形的内部,当问题中已知内心时,情况单一。若外心已知,但图未给出,则我们在画图时,要注意三角形的外心可能在形内、形上或形外,要分类讨论。
例3 △ABC的外心为O,且∠BOC=110°,则∠BAC= 。
【解析】本题考查圆的外心的知识、圆周角定理、分类思想。若点O在△ABC内,如图8,则∠BAC=∠BOC=55°。若点O在△ABC外,如图 9,则∠BAC=·优角∠BOC=×(360°-110°)=125°。所以∠BAC=55°或125°。
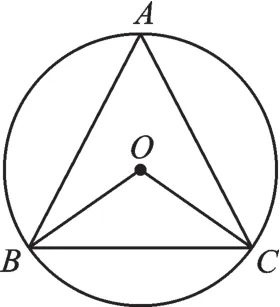
图8

图9
【点评】因为题目中未给出图形,所以需要我们画出图形,根据外心的可能位置分类讨论。我们要考虑是否有多种可能,从而避免漏解。
8.直线与圆相切。
直线与圆相切的判定方法有三种:有唯一公共点;用d与r的关系来探求(d是圆心到直线的距离);直线经过半径的外端并且与这条半径垂直。问题通常分为两大类:一是直线与圆没有公共点,二是直线与圆已知公共点。若没有公共点,则过圆心作直线的垂线,证明d=r。若直线与已知圆有公共点,则连接过公共点的半径,证明直线垂直于该半径。
例4 如图10,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,求证:⊙D与OA相切.
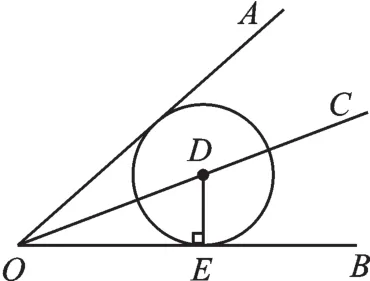
图10
【解析】直线OA与⊙D没有已知的公共点,只能利用“圆心D到直线OA的距离等于⊙D的半径DE”,说明⊙D与OA相切。
证明:过点D作DF⊥OA于F,如图11。∵点D是∠AOB的平分线OC上任意一点,DE⊥OB,DF⊥OA,∴DF=DE,即D到直线OA的距离等于⊙D的半径DE。∴⊙D与OA相切。
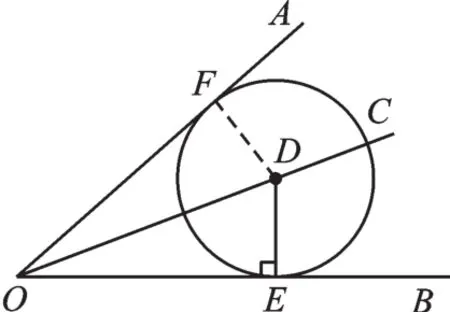
图11
【点评】此题考查了切线的判定与角平分线的性质,难度不大,解题的关键是准确作出辅助线。既然没有给出公共点,则不能连接过公共点的半径,运用“经过半径的外端并且垂直于这条半径的直线是圆的切线”来证明。我们要学会根据不同类型,选择恰当方法,尤其不要忘记d=r这种基本判别方法。
9.其他两解情况。
(1)过圆外一点引圆的切线,有两条,不能漏解。
(2)已知两条平行弦(非直径),长度确定,若图形未给出,则两条平行弦的位置有两种情况,两条弦位于圆心的同侧或位于圆心的两侧。



