于逸林
(陕西师范大学附属中学 710061)
文中针对2017年全国数学高考二卷第23题的第二问,除了标准答案的两种解法外,探究了另外七种新解法;并在本题启发下,引深拓展了四道新题目及新结论.
一、原题
已知a>0,b>0,a3+b3=2.
证明:(2)a+b≤2.
标准答案两种解法,分别为:
解法1 因为(a+b)3=a3+3a2b+3ab2+b3
=2+3ab(a+b)
所以(a+b)3≤8,因此a+b≤2.
解法2 反证法.
若a+b>2,则a3+b3>(2-b)3+b3
=2+6(1-b)2
≥2
与题设矛盾,所以a+b≤2
二、作者的七种不同解法
1.使用着名不等式的解法
解法1 由排序不等式
a3+b3≥a2b+ab2.
∴(a+b)3=a3+3a2b+3ab2+b3
≤4(a3+b3)=8,
∴a+b≤2.
解法2 由柯西不等式,有
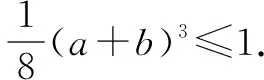
从而a+b≤2.
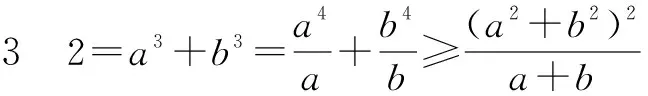
所以a+b≤2.
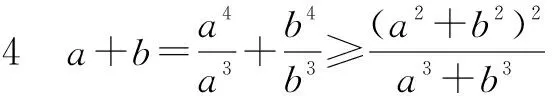
所以a+b≤2.
2.利用函数性质的解法
解法5 当a=b=1时,结论显然成立.
当a≠b时,由a3+b3=2知a,b中有一个>1,一个<1,
故不妨设a>1>b.
则a3+b3=2
⟺a3-1=1-b3>0.
而a+b≤2
⟺a-1≤1-b
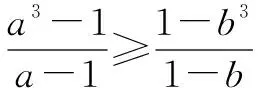
⟺a2+a+1≥b2+b+1.
又因为f(x)=x2+x+1在(0,+)是增函数,
故a2+a+1≥b2+b+1⟺a≥b.
从而由a>1>b知结论成立.
解法6 注意到当x>0时有
x3-3x+2=(x-1)2(x+2)≥0,
有x3≥3x-2.
故2=a3+b3≥3(a+b)-4,
从而a+b≤2.
3.使用增量代换的解法
解法7 由a3+b3=2,可知a,b中有一个≥1,一个≤1.
故不妨设a≥1≥b,
设a=1+λ,b=1-μ.
则a3+b3=2
⟺3λ+3λ2+λ3=3μ-3μ2+μ3
⟺3λ+λ3+3(λ2+μ2)=3μ+μ3,
∴3λ+λ3≤3μ+μ3.
又由f(x)=x3+3x为增函数得λ≤μ,
故a+b=1+λ+1-μ≤2.
依据此题目,还可推理得到如下结论:
(拓展1)
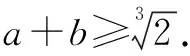
此题难度不是太大,注意到可用ab≥0进行放缩便可得到以下解法.
证明由于(a+b)3=a3+3a2b+3ab2+b3
≥a3+b3=2,
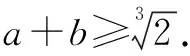
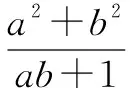
此题难度较大,可采用先猜后证的方法.
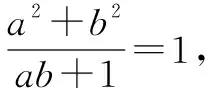
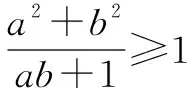
下面证明该不等式
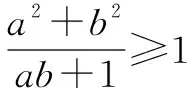
⟺a2+b2≥ab+1
⟺a2-ab+b2≥1.
又由于a3+b3=2,0
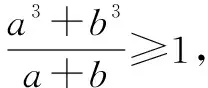
即a2-ab+b2≥1,上式得证.
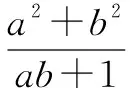
(拓展3)已知a≥0,b≥0,a3+b3=2,求证:a2+b2≤2.
证明由柯西不等式,有
4=2(a3+b3)≥(a+b)(a3+b3)
≥(a2+b2)2,
故a2+b2≤2.
(拓展4)已知a≥0,b≥0,a3+b3=2,求证:|a3-b3|≤3|a-b|.
证明当a=b时,结论显然成立
当a≠b时,
|a3-b3|≤3|a-b|
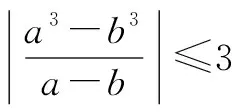
⟺a2+ab+b2≤3.
又由基本不等式,有a2+b2≥2ab,
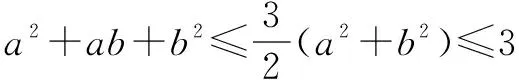
因此|a3-b3|≤3|a-b|
由以上的解法及拓展可以看出,这道题有多种思考方向,高中数学及竞赛数学中证明不等式的大部分常用解法也已被以上的分析所包含,如:利用基本不等式、柯西不等式,以及其它着名不等式进行证明;反证法证明不等式;多变元转换为单变元;利用函数单调性证明;利用平方的非负性进行证明;使用增量代换进行证明;取等条件特殊的不等式解法(例如利用ab≥0,a≤a+b,b≤a+b等进行放缩)以及先猜后证的方法等,希望对读者解题有所帮助与启发.
(指导教师:陕西师范大学 倪如俊)



