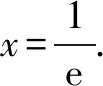许银伙 杨苍洲
(1.福建省泉州外国语中学 362000;2.福建省泉州第五中学 362000)
压轴题中有时出现三角函数与对数函数或指数函数结合的不等式或求零点问题,这类问题通常综合程度较高,整体解决难度较大.可以利用图形直观引领,帮助寻找思路,结合三角函数的周期性、有界性和单调性,分段讨论,让问题获得圆满的解决.
例题1(2019年全国理科卷Ⅰ)已知函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数.证明:
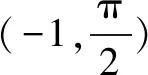
(Ⅱ)f(x)有且仅有2个零点.
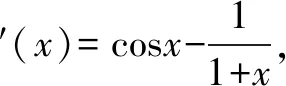
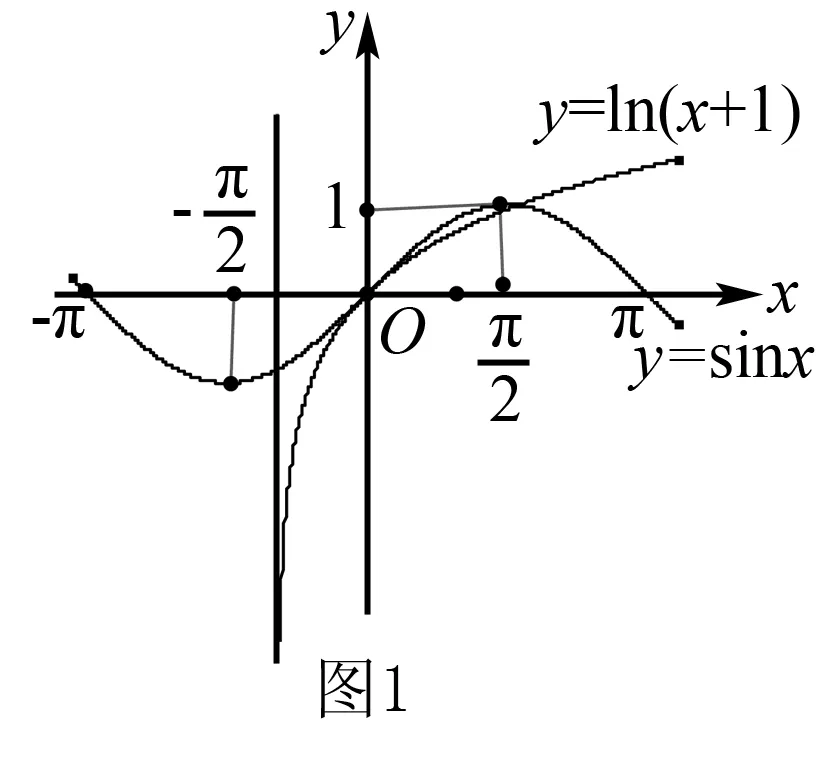
(Ⅱ)分析:f(x)=0,即sinx=ln(1+x),作函数y=sinx和y=ln(1+x)图象,由图看出:当x∈(-1,0)时,sinx>ln(1+x),即f(x)>0;
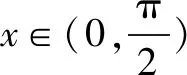
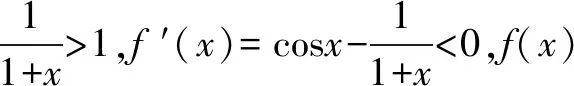
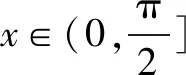
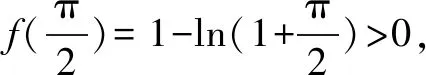
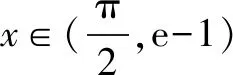
(4)当x∈[e-1,+)时,f(x)=sinx-ln(1+x)<1-1=0恒成立,无零点.
综上所述:f(x)有且仅有2个零点.
反思与评注1.函数f(x)中含有两个超越函数sinx和ln(1+x),都很容易分别作出函数图象,因此可以借助图象帮助寻找解决思路.
2.客观题中的零点问题,基本上都是用数形结合解决的,对于主观题可以借助数形结合帮助寻找思路,然后把解答书写完整.
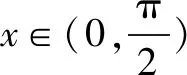
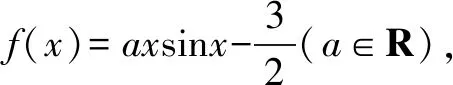
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)判断函数f(x)在(0,π)内的零点个数,并加以证明.
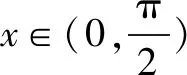
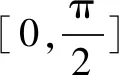
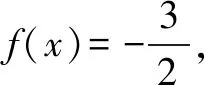
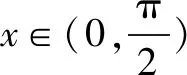
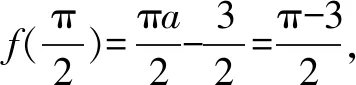
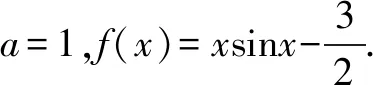
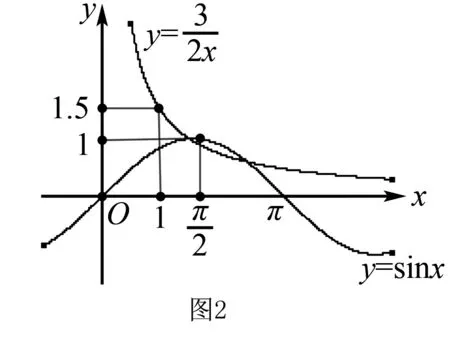
(Ⅱ)函数f(x)在(0,π)内的零点个数为2.
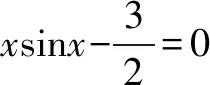
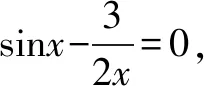
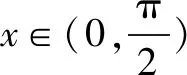
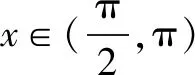
综上所述:函数f(x)在(0,π)内的零点个数为2.
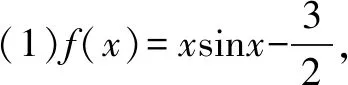
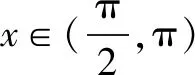
综上所述:函数f(x)在(0,π)内的零点个数为2.
反思与评注1.问题(Ⅱ)的方法一和方法二都是分区间解决,但方法一借助图象引领,思路更明确.
2.相比例1,本题利用图象可以直观看出有两个零点,但解答过程需要完整规范地书写.
3.从命题的角度看,例1比例2优秀,例2借助图象可以毫无悬念地获得准确答案,例1不通过计算无法说清楚.
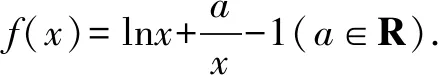
(Ⅰ)若函数f(x)的最小值为0,求a的值;
(Ⅱ)证明:ex+(lnx-1)sinx>0.
分析与解(Ⅰ)a=1.
(Ⅱ)分析:不等式ex+(lnx-1)sinx>0中含有三个超越函数,它们的公共允许值范围是(0,+).ex∈(0,+),函数sinx具有周期性,sinx∈[-1,1],当x∈(0,e)时,lnx-1<0;当x∈(e,+)时,lnx-1>0.当x足够大时, ex函数值会指数爆炸,lnx-1的函数值是缓慢增长,所以当x足够大时,可以把sinx用-1代入尝试.因此证明的难点是当x处于0的右侧附近时如何处理,考虑到当x∈(0,+)时,有sinx 证明令g(x)=ex+(lnx-1)sinx,x∈(0,+). (2)当x∈[e,+)时,lnx-1≥0,sinx∈[-1,1],所以g(x)≥ex-(lnx-1). 由ex-x>1对x>0恒成立可得:x>ln(x+1)对x>0恒成立,所以lnx 综上所述:ex+(lnx-1)sinx>0恒成立. 反思与评注1. 当x∈(0,e)时,lnx-1<0,sinx∈[-1,1],若利用g(x)>ex+lnx-1,取x=e-2,ex+lnx-1 2.本题的解决对观察与分析,动手实践,基础知识以及常用结论的应用能力有较高要求. 例题4 (2017年山东理科卷)已知函数f(x)=x2+2cosx,g(x)=ex(cosx-sinx+2x-2),其中e=2.71828…是自然对数的底数. (Ⅰ)求曲线y=f(x)在点(π,f(π))处的切线方程; (Ⅱ)令h(x)=g(x)-af(x)(a∈R),讨论h(x)的单调性,并判断有无极值,有极值时求出极值. 分析与解(Ⅰ) 切线方程为:2πx-y-π2-2=0. (Ⅱ)h(x)=g(x)-af(x),即h(x)=ex(cosx-sinx+2x-2)-a(x2+2cosx),可得:h′(x)=2(x-sinx)(ex-a)(x∈R),且h′(0)=0.令φ(x)=x-sinx,则φ′(x)≥0,φ(x)在x∈(-,+)单调递增, 又φ(0)=0,则当x<0时,φ(x)<0,x-sinx<0;当x>0时,x-sinx>0. (1)当a≤0时,ex-a>0对x∈R恒成立.可得:当x<0时,h′(x)<0;当x>0时,h′(x)>0.函数h(x)在(-,0)单调递减,在(0,+)单调递增,h(x)有极小值h(0)=-1-2a,无极大值. (2)当a>0时,由h′(x)=0得:x1=0和x2=lna. ①当lna<0,即00解得:x ②当lna>0,即a>1时,利用右图4,由h′(x)>0得:x<0或x>lna;由h′(x)<0得:0 ③当lna=0,即a=1时,h′(x)≥0(当且仅当x=0时取等号),h(x)在(-,+)单调递增,h(x)无极值. 反思与评注1. 由h′(x)=2(x-sinx)(ex-a)讨论h(x)的单调区间,首先是求出h′(x)的零点,其中φ(x)=x-sinx单调递增,且φ(0)=0是常用结论,应该记住. 2. 当a>0时,分别找出y=x-sinx和y=ex-a的零点,利用它们都是递增函数,作出草图可快速求出h′(x)=2(x-sinx)(ex-a)正负值的符号区间,化一为二,形象直观.