赵爱华 李昌成
(1.新疆乌鲁木齐市教育研究中心 830002;2.新疆乌鲁木齐市第八中学 830002)
一、题目呈现
题目(2021年普通高等学校招生全国八省演练联考,T22)已知函数f(x)=ex-sinx-cosx,g(x)=ex+sinx+cosx.
(2)若g(x)≥2+ax,求a.
二、总体认识
1.略.2.本题较为新颖,通过基本初等函数之指数函数与正余弦函数和带参一次函数命制成压轴题,考查导数的重要知识,单调性、极值、最值、切线方程等.合理应用等价转化、分类讨论、数形结合等数学思想解题非常关键.学生只有在基础扎实,技能娴熟的能力条件下,方可正确解答.本题还有一个创新点,定义域为全体实数,失去边界效应.本类试题在以往的高考中,定义域多为(-∞,m]或[m,+∞)或(-∞,m)或(m,+∞)型.
三、解法探究
1.从极值入手
分析1 将g(x)≥2+ax变形成g(x)-2-ax≥0,此题可以看作是一个利用函数极值与最值关系求值的问题.通过等价转化,问题可以解决.
解法1 由g(x)=ex+sinx+cosx,g(x)≥2+ax,得
ex+sinx+cosx-2-ax≥0.
令φ(x)=ex+sinx+cosx-2-ax,
原问题等价转化为φ(x)≥0=φ(0)恒成立.
则φ′(x)=ex+cosx-sinx-a.
因为定义域为R,又φ(x)≥0=φ(0),因此最小值φ(0)一定是极小值,所以0必须是φ(x)的极值点.
于是φ′(0)=0,解得a=2.
事实上,当a=2时,φ(x)≥0恒成立,下面证明之.
当a=2时,φ(x)=ex+sinx+cosx-2-2x,
φ′(x)=ex+cosx-sinx-2,
φ′′(x)=ex-sinx-cosx.
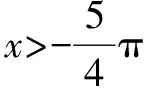
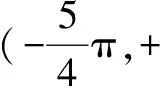
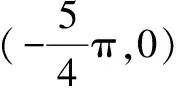
结合函数y=ex的性质,知
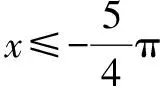
所以当a=2时,φ(x)≥0恒成立.
评析显然此解法较为繁琐,尤其是充分性的证明,我们非常有必要再探索新途径,寻找新解法.
2.利用排除法
分析2φ(x)=ex+sinx+cosx-2-ax在0处导函数值φ′(0)只有三种可能性,φ′(0)>0,φ′(0)<0,φ′(0)=0,通过计算论证排除两种,第三种必然成立.
解法2 结合解法1,知φ′(x)=ex+cosx-sinx-a.
若φ′(0)>0,即2-a>0,解得a<2,则∃x0<0,使得φ′(x0)=0,于是x∈(x0,0)时,φ′(x)>0.
那幺φ(x)在(x0,0)上单调递增,所以φ(x0)<φ(0)=0,此与已知矛盾;
同理,若φ′(0)<0,即2-a<0,解得a>2,则∃x1>0,使得φ′(x1)=0,于是x∈(0,x1)时,φ′(x)<0.
那幺φ(x)在(0,x1)上单调递减,所以φ(x0)>φ(0)=0,此也与已知矛盾.
所以φ′(0)=0,即2-a=0,解得a=2.
3.借助导数定义求解
分析3 按x=0,x>0,x<0分类讨论问题,先求a的几种范围,再求交集得解.
解法3 由g(x)=ex+sinx+cosx及g(x)≥2+ax,得
ex+sinx+cosx-2≥ax.
(*)
(1)当x=0时,(*)中等号成立,a∈R.
(2)当x>0时,(*)变形为
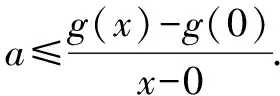
(3)当x<0时,(*)变形为
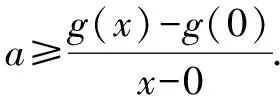
综上,a=2.
4.数形结合,挖掘本质
分析4g(x)≥2+ax恒成立,其本质是左边的曲线始终不在右边的直线之下,而a恰好是右边直线的斜率,因此我们需要寻找临界位置——切线.
解法4 因为g(0)=e0+sin0+cos0=2,所以曲线y=g(x)和直线y=2+ax都经过定点(0,2).结合函数图象,只有当直线y=2+ax在(0,2)处与y=φ(x)相切才满足题意.否则,若直线与曲线相交,则不满足题意.
由导数的几何意义,得g′(0)=a.
由g(x)=ex+sinx+cosx,得g′(x)=ex+cosx-sinx.
所以a=e0+cos0-sin0=2.
评析本解法实质是借用了y=φ(x)在0附近的凹凸性,记g(x)=ex+sinx+cosx的最大负零点为t,当x∈(t,+∞)时,y=φ(x)是凹函数,y=2+ax与g(x)=ex+sinx+cosx才满足题意.这对中学生而言有一定的难度.
四、题型溯源
题1(2017年全国高考数学Ⅱ卷理科第21题第(1)问)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0,求a.
注由于x>0,f(x)≥0,即ax2-ax-xlnx≥0,进而a(x-1)≥xlnx.这就是本题的同类题型了,y=xlnx的单调性较为清晰.同时,本题的端点值0具有提示作用,降低了难度.
题2(2017年全国高考数学Ⅱ卷文科第21题第(2)问) 设函数f(x)=(1-x2)ex.当x≥0时,f(x)≤ax+1,求a的取值范围.
注因为f(x)=(1-x2)ex在x∈[0,+∞)上是凸函数,故条件“x≥0时,f(x)≤ax+1”等价于“射线y=ax+1(x∈[0,+∞))位于曲线f(x)=(1-x2)ex在点x=0处的切线位置或其上方”.关键在于临界位置——切线,这是本质所在.
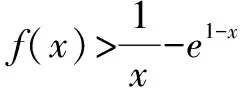
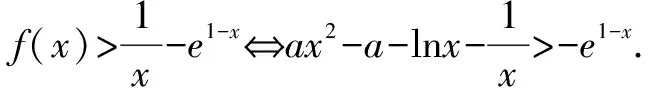
数形结合是突破这类题的关键,尤其是曲线与直线相切的恰当使用.试题兼顾了基础性、综合性、创新性和综合性.题目从“知识立意、能力立意”向“价值引领、素养导向”转换,体现了高考的引导作用、选拔功能.刷题决不能突破这个层次的题目,我们的教学务必在能力和素养上下功夫.



