李晓明


谈到“对弈游戏”,我们很容易马上想到的是各种棋艺。说到棋艺,简单的有对角棋,复杂的有象棋、围棋等。编写会下棋的计算机程序,几乎是计算机创始之初人们就有的追求。1958年,在中国的哈尔滨工业大学,曾经就研制出一台“能说话,会下棋”的模拟计算机(如图1)。
1997年,IBM的深蓝战胜了国际象棋大师卡斯帕罗夫,引起一阵轰动。2016年,谷歌的AlphaGo战胜了围棋世界冠军李世石,让人们终于见证了计算机在棋艺领域已经可以稳定表现出高于人类的智能。这极大地提振了人们对计算机智能应用的信心,人工智能迎来了一个新的发展高潮。
计算机表现出来的任何智能的核心都是算法:有的是若干经验规则的编码(如中医诊断),有的是基于自然界或社会生活带来的启发式(如陈道蓄教授在本专栏前面介绍过的模拟退火),有的需要先从大量数据中学习出一些模式(如当下广泛应用的人脸识别),还有的则可能是基于对问题的深刻理解形成的小巧精妙的计算。下面要讨论的一种两个人玩的对弈游戏,就是后面这种情形的一个实例。①
● 游戏介绍
也许读者玩过下面这个游戏:有两堆棋子,第一堆3颗,第二堆5颗。两人轮流拿,每次只能从一堆中拿,至少拿一颗,拿到最后一颗棋子的为胜者。假设你是先手,希望获胜。该怎么拿?
如果你一次把第二堆全拿走,对手则可以接着把第一堆全拿走,他胜了。如果你第一次只从第二堆拿走4颗,留下1颗,对手则可以接着从第一堆拿走2颗,留下1颗。你发现又要输了。不过稍微想一想,你马上能意识到这里的制胜法则:总给对方留下棋子数相同的两堆。于是,你从第二堆拿走2颗作为开始,剩下(3,3)。后面,对手从某一堆拿走几颗,你就从另一堆拿走几颗。两个回合下来,对手就会认输了。显然,如果初始第一堆和第二堆棋子数分别是n1和n2,只要n1≠n2,你作为先手按照上面的策略就能保证赢。而如果n1=n2,你作为先手就只能随便拿几颗,把赢的希望寄托在对手不明白这法则了。
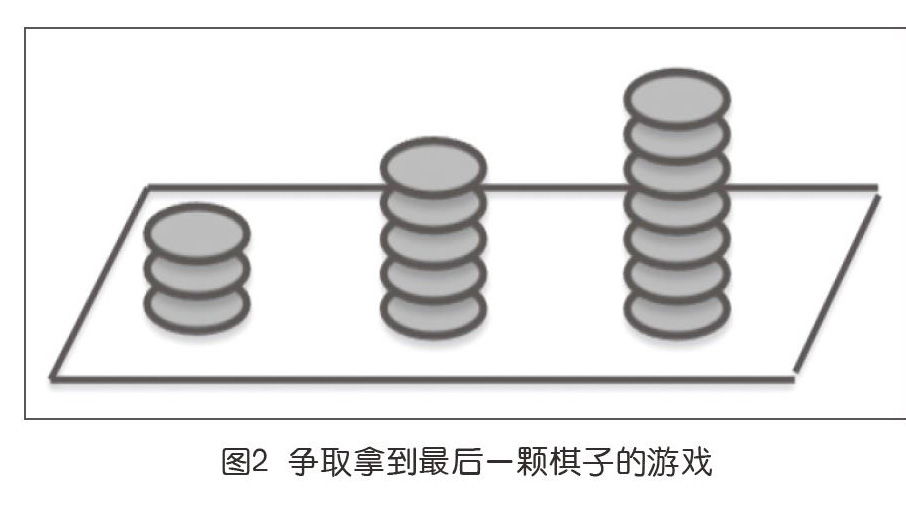
下面,我们前进一步:考虑有三堆棋子(如下页图2),数量记为(3,5,7)。规则一样,目标也一样,你是先手,该怎么拿?
显然,你不应该一开始就拿走一整堆,那样就让对方处于在两堆情形下的先手优势了。好,那你就从第三堆里拿走6颗,给他留1颗,于是变成(3,5,1)。可如果他的应对是从第二堆里拿走3颗,留下2颗,成为(3,2,1),你接着该怎么办呢?稍微想一想,你会发现该认输了!
于是你面对两个问题。第一,在这个对弈游戏中,是否存在一个先手胜的法则?第二,如果存在,它是什么?
● 一般情形下的通解
下面,我们来讨论这个问题的最一般的形式,然后看到对这个问题的解可以用一个小小的程序实现为“AI”,作为游戏的一方,你可以找一个朋友来和它玩,它不保证一定赢,但只要抓住了对手的“破绽”,它就不客气了。
问题描述:给定m堆棋子,分别有n1,n2,……,nm颗,ni≥1。两个玩家轮流从中取棋子,每次只能从一堆拿,至少拿一颗,谁拿最后一颗谁为胜。②是否存在先手胜的条件?如果存在,它是什么?
让我们先看看m=2的情形。其实前面已经有解了,即先手胜的条件是n1≠n2,做法是总让两堆棋子相等。让我们再细细体会一下。
这里,n1和n2是否相等是关键。有两个层次的含义。如果不相等,先手就可将局面做成相等,后手返回的局面则一定是不相等的,于是可以一直在这种交替性质下继续。先手做的总是“不相等”→“相等”,后手则总是“相等”→“不相等”。而结束的局面是两堆都为0,是相等局面,因此必由先手导致,也就是先手拿了最后一颗棋子。而如果n1=n2,由于每次至少要拿走一颗棋子且只能从一堆拿,先手给出的局面只能是两堆不相等的,也就是不得不让后手得到上述有利局面。
现在我们面对的是m>2个数,n1,n2,……,nm。相等与否,这种最简单的计算概念已经不好用了。但在这m个数中能不能建立一种计算,在某种性质上呈现满足与否的状态,一旦先手发现这种性质满足,他总能通过从某一堆中拿掉若干棋子,使得剩下的数之间不再满足该性质,并且后手做任何动作返回的局面又将满足该性质。而结束局面是全为0,是不满足该性质的,因而必然为先手导致。
幸运的是③,计算机科学中有一种重要的逻辑运算——异或,它将给我们带来所需的性质。具体而言,下面来看Python中正整数按二进制位异或操作(^)的运用。读者可通过图3中几个例子来复习一下。
例如④:3^5^7=(011)2^(101)2^(111)2=(001)2=1。简言之,若干0和1异或操作的结果由其中1的个数的奇偶性决定,偶数为0,奇数为1。注意,对应位进行运算,位和位之间不相干。
设想参照图3所示例子的样子,考虑m个非负整数n1,n2,……,nm的按位异或。结果总是可以按照是否为0(数值)做二元区分。例如,3^5^7=001=1≠0,2^5^9^14=0010^0101^1001^1110=0000=0。特别地,当m=2时,异或为0,当且仅当两个数相等。
n1^n2^……^nm结果为0,意味着所操作的每一个二进制位对应的m个0/1中1的个数都是偶数。还意味着其中任何单个ni有任何变化,都将导致异或结果不再为0。⑤读者此时应该可以看到了一些希望。即,如果先手面对的是“结果不为0”局面,且有办法通过拿掉若干棋子,给后手一个“结果为0”的局面,那么无论后手怎么做,他返回的一定是一个“结果不为0”的局面。
于是,我们就看到了先手做“结果不为0”→“结果为0”,后手则不得不做“结果为0”→“结果不为0”的重复模式。注意到结束局面是全为0,即“结果为0”,因而必为先手所致,意味着最后一颗棋子是他拿的。这样,“结果不为0”,就是先手希望一开始就看到的性质。
剩下一个关键问题:当面对一个“结果不为0”的局面,先手总能通过拿掉若干棋子将它变为“结果为0”局面吗?对应前面m=2的情形,那是要将两个不相等的变成相等的,比较一目了然。现在则需要一点“计算”了。
设x=n1^n2^……^nm≠0,我们需要做的是找到一个ni,让它减少一些,使得在异或的结果为0。例如,001=011^101^111=3^5^7,如果做7→6,就有3^5^6=011^101^110=0了。
一般地,由于x^x=0,即两个相等的数异或总为0,于是也就有n1^n2^……^nm^x=0,注意到异或操作满足交换律,问题就变成能否找到一个ni,满足0≤ni^x 这样的ni总是存在的。凡在x的二进制表示最高位1的位上也是1的ni都符合条件。⑥ 这是因为,那样的ni一旦与x做按位异或操作,ni^x对应x最高位1的那一位就是1^1=0了;而由于那个1是x的最高位1,ni^x中更高的位就和ni保持相同,这就保证了ni^x 至此,我们完整研究了这种对弈游戏的玩法。你可以写一个AI算法了,核心如图4所示。 当然,为了达成一个实际可与你的客人玩一玩的程序,你还需要做些外围处理,例如,可以让客人任意选择初始的m个数,n1,n2,……,nm,包括m本身,以及让他为先手。游戏过程本质上就是他和你的程序交替按游戏规则改变那些数,直至全部为0。最后一步的执行者就是赢家。显然,如果他也是懂得这其中道理的,那么在某些初值条件下(如她为先手,并且初始m个数的异或不为0)有可能会赢了你的AI程序。但只要他中间犯一次错误,就再也没有机会了。 鼓励有兴趣的读者自己实现这个AI程序。如果感觉有较大困难,也欢迎和我们联系。下页图5是我的程序的运行界面,供参考。 ● 进一步讨论 不难认识到,异或运算的性质在求解这个问题中起到了关键作用。事实上,异或运算定义简单,但功能奇妙。例如,假设要在程序中交换两个整数变量a和b的值。通常的做法是用一个中间变量tmp,做tmp←a; a←b; b←tmp。如果利用按位异或操作,也可以是: a=a ^ b # 得到初始a和b的异或值 b=a ^ b # 现在b中就是初始a的值了,因为(a^b)^b=a a=a ^ b # 现在a中就是初始b的值了,因为(a^b)^a=b 这样一种“节省一个存储单元”的做法,在过去存储很珍贵的年代是有实际意义的。异或运算在信息加密、数据结构等方面也都有出色的应用。不仅如此,异或概念在现实生活中也有用。例如,有些场合一盏灯是由两个开关控制的,即所谓双控开关。进门按一个开关B1,灯亮了,进屋后按另一个开关B2,灯灭了;再按B2,灯又亮了,出门时再按B1,灯就灭了。这就是异或逻辑在背后起作用。 在前面讨论通解时,我们体验了一种逻辑运算和算术运算“混合作用”的场景。即一方面将数据对象分别看成是0/1字符串,执行按对应位置的逻辑运算,另一方面又将那样的0/1字符串看成是“数”,从而可以比较大小。初次接触这种情境的读者可能会有些困惑,但这个例子恰恰很好地展示了计算机进行“计算”的要义,即表示、变换和解释。具有某种含义的信息通过编码表示为数据,对该数据进行操作变换得到中间数据和结果数据,结果数据再通过适当解释得到符合需要的含义。在这个过程中,同一个数据可以有不同的解释,有些解释可能更加便于达到计算的最终目的。 最后,我们说按照上述通解编出的程序,在和人对弈的过程中,显然会表现出“智能”——它能“随机应变”,因此,也可以称为是一个“人工智能程序”。它的智能基于知识(如异或运算的性质)和对问题本身的理解,而不是基于数据的,也就是不同于现在流行的通过机器学习得到的智能。在此强调这一点,是想告诉读者,人工智能是一个广阔的领域,不限于大数据基础上的机器学习,尽管后者十分重要且当下正是大力发展的机遇窗口期。 释: ①此例受参考文献[1]中第226个问题的启发。该问题的具体呈现形式为棋子的移动,本文等效呈现为棋子的拿取。同时,本文在朋友间传阅过程中,湖州师范大学的邵斌老师指出2006年全国青少年信息学奥赛中有一个类似的题目。 ②在本文待发表期间,也考虑了一个相反的问题,即“拿最后一颗者为输”,是否也存在先手胜的条件。在课堂上和学生提起,李夏鲲同学当晚就给出了一个条件和证明。读者读过本文后,也能想出那个反问题该怎么解决吗? ③下面讨论的通解方法,不是本文作者的发明。我依稀记得很久前在某个材料上看过(但忘了出处),写这篇文章时只是做了回顾整理的工作。 ④这个例子中,我们特别用下标2表示是二进制数。在不至于混淆的情况下,后面的例子将省略这种表示,以求简洁明了。 ⑤这一个认识可以这样体会:ni改变,它的二进制表示中总会有某些0变成1或者某些1变成0,于是就会破坏前面所说异或为0,必有每个二进制位上1的个数为偶数的条件。 ⑥即,若记x=x1x2…xk…xt为x的二进制表示,如果xk=1,所有xi=0,i<k,这个k就是这里关注的位。 参考文献: [1](苏)柯尔詹姆斯基.趣味数学[M].张继武,程韬,译.北京:少年儿童出版社,1961,5. [2]Maaz.XOR–The magic bitwise operator[DB/OL].http://kackernoon.com. 注:作者系北京大学计算机系原系主任。



