具有N-策略和延迟单重休假且休假不中断的M/G/1排队系统

何亚兴，唐应辉

(四川师范大学数学科学学院，四川 成都610068)

1.引言

在对具有经典N-策略、T-策略、D-策略控制的排队模型的研究基础上[1-8]，随着研究的深入和实际应用，一些具有联合控制的排队模型也得到了学者们的关注[9-18].文[9]把N-策略和服务员多重休假结合，研究了有Min(N，V)-策略控制的M/G/1排队系统，而且服务员的休假是可以中断的，即在服务员的假期中，如果到达的顾客数达到事先设定的正整数阈值N，服务员立即中断该次休假回到系统为顾客服务，这种在服务员的休假可以中断的情况下，系统在达到稳态时服务员忙期开始的顾客数不超过N个，文[9]利用稳态队长的随机分解结构给出了稳态队长分布的概率母函数，从而得到平均队长的表达式.文[10]继续讨论该模型，不仅讨论了从任意初始状态出发的瞬态队长分布，获得了瞬态队长分布关于时间t的Laplace变换表达式，而且使用洛必达法则，经过简单计算获得了稳态队长分布的递推表达(通过母函数是很难得到稳态队长分布的表达式的)，而获得便于做数值计算的稳态队长分布表达式在系统容量的优化设计中有重要意义.文[11]把N-策略与服务员的单重休假结合起来，研究了服务员具有单重休假且休假可中断和系统采取Min(N，V)-策略控制的排队系统.文[12]从任意初始状态出发，详细研究了具有Min(N，D)-策略控制的M/G/1排队系统，其中服务员具有多重休假且休假可中断，应用更新过程理论和全概率分解技术，不仅得到了系统队长的瞬态分布关于时间t的Laplace变换表达式，而且得到了便于作数值计算的队长稳态分布的递推表达式，并通过队长稳态分布的数值计算讨论了系统容量的优化设计问题，然后在建立费用结构模型基础上，通过数值计算例子讨论了最优控制策略(N*，D*).文[13]将Min(N，V)-策略引入到离散时间的Geo/G/1排队系统中.文[14]把N-策略和服务员多级适应休假结合，推广了文[9-11]的研究模型.由于服务设备(服务台)在运行过程会因为老化磨损等原因发生故障，因此文[15]研究了具有温储备失效特征和单重休假Min(N，V)-策略的M/G/1可修系统排队系统，并用数值计算例子讨论了最优控制策略N*.文[16-17]和[18]分别将N-策略、D-策略和服务员的单重(多重)休假机制结合，引入具有二维策略控制的Min(N，D)-控制策略，提出建立了系统具有Min(N，D，V)-策略控制的M/G/1排队系统模型.

但是，在以上有策略控制和服务员休假机制的排队系统研究中，大多文献都假定服务员根据系统所采取的控制策略可中断休假.事实上，在实际中情况并非完全如此，例如服务员休假的地方离工作单位较远，或者所从事的辅助工作不能立即中断，此时需等待服务员长途归来或完成辅助工作后才能回到系统为顾客服务.文[8]研究了N-策略和服务员单重休假且休假不中断的M/G/1排队系统模型，运用更新过程理论，全概率分解技术和Laplace变换工具，研究了系统队长的瞬态分布和稳态分布，但有关结果是错误的.另外，在我们的实际生活当中，有很多的休假排队系统是在服务员完成服务和系统变空以后，不能立刻去休假的，而是要经过一段准备休假的延迟时间，这段时间是很有必要的，如银行或者很多商店在下班之前，会清点一下账目或清点货物或者整理器材等等，如果在这一段时间又有顾客到达，为了不损失顾客和提升信誉，他们又会接待顾客，接待完以后，又得重新清点账目或者整理器材，直到清点完以后也没有顾客到达，才开始去休假.因此，基于上述，本文把“延迟休假”、“N-策略”、“服务员单重休假且休假不中断”这三者结合，提出建立如下排队系统模型:

1) M/G/1型的排队系统:顾客相继到达的时间间隔τ有分布F(t) = 1-e-λt，顾客的服务时间χ是任意分布G(t)，记平均服务时间为1/µ(0 ＜µ＜∞);

2) 服务员采取延迟单重休假且休假不中断机制，服务的启动是实行N-策略控制:每当系统变空时，服务员不是立即去休假，而是有“延迟时间”Y(随机的)，“延迟时间”Y 服从任意分布Y(t).如果有顾客在延迟时间Y 内到达，服务员立即为顾客服务，直到系统再次变空再重新做休假准备; 如果没有顾客在延迟时间Y 内到达，则延迟时间结束以后服务员立刻去休假一次，休假时间V 服从任意分布V(t).当服务员休假转来，系统中等待服务的顾客数大于或者等于事先设定的正整数阈值N个，服务员立刻启动系统设备为顾客服务，直到系统再次变空; 若发现系统中等待服务的顾客数小于N个，则服务员就待在系统中处于空闲状态(在岗)直到系统内到达顾客数达到N个再启动系统设备为顾客服务;

3) 所涉及随机变量τ、χ、Y、V 是相互独立的.

另外，根据实际情况，进一步假设在t = 0时，如果系统中无顾客，服务员就待在系统中直到第一个顾客到达，而且立即服务，也就说，只有在服务员繁忙一段时间以后才实行延迟单重休假且休假不中断机制和系统启动服务的N-策略控制(这种假设更符合实际情况).

2.队长的瞬态分布和稳态分布

首先，一个“系统闲期”是指从系统刚变空的时刻起，直到其后第一个顾客到达的时刻为止的这一段时间.如果用表示第j个“系统闲期”长度，则由于到达过程为参数λ(＞0)的Poisson过程易知“系统闲期”的分布为=F (t)=1-e-λt，j ≥1.

其次，一个“服务员忙期”是指从服务员开始为顾客服务的时刻起，直到系统再次变空为止的这一段时间.若令b表示该系统从一个顾客开始的“服务员忙期”长度，B(t)=P {b ≤t}，则有如下引理:

引理2.1[6]对ℜ(s)＞0，b(s)是方程z =g(s+λ-λz)在|z|＜1内的唯一根，且

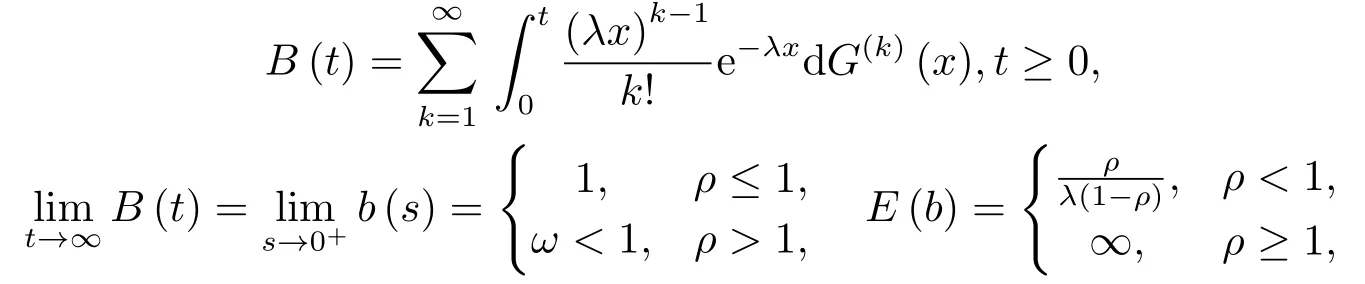
注2.1N(t)表示系统在时刻t的队长，即时刻t在系统中的顾客数;与分别表示相应G(t)的拉普拉斯(L)变换和拉普拉斯-斯蒂尔切斯(LS)变换;G(k)(t)表示相应G(t)的k重卷积，

令b〈i〉表示从i个顾客开始的“服务员忙期”长度，因为到达过程是泊松过程，所以有分布P{b〈i〉≤t}=B(i)(t)，t ≥0，i ≥1.

又令Qj(t) = P {b ＞t ≥0;N(t)=j}表示在“服务员忙期”b中队长为j的瞬态概率，且t=0时只有一个顾客，“服务员忙期”b刚开始，即Q1(0)=1，Qj(0)=0，j ＞1.

引理2.2[6]令为Qj(t)的L变换，对ℜ(s)＞0和j ≥1，有

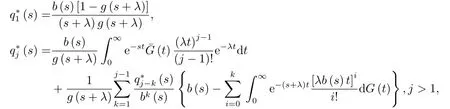
下面讨论系统队长的瞬态和稳态的概率分布.令pij(t) = P {N(t)=j|N(0)=i}表示在初始时刻有i个顾客的条件下，在时刻t队长为j的瞬态概率，

定理2.1对ℜ(s)＞0和i ≥1，有

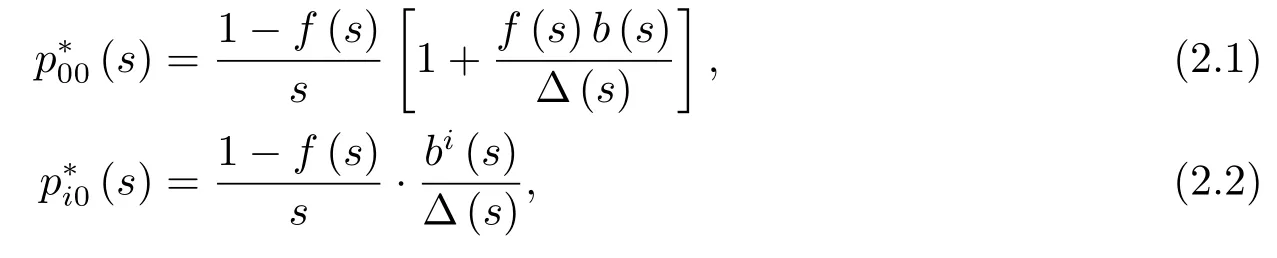
其中

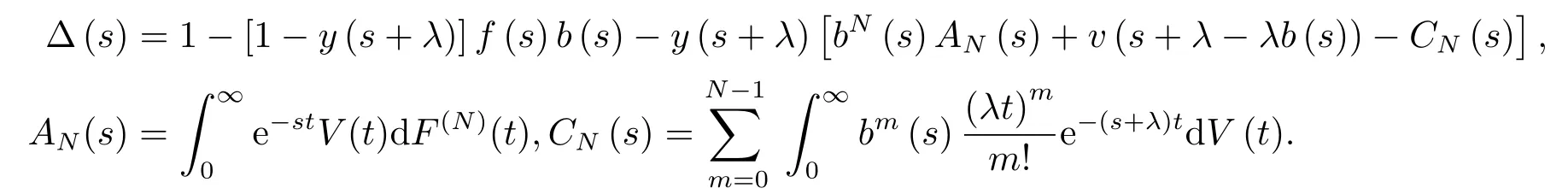
证令显然队长为零的充要条件是时刻t处于系统闲期中，运用全概率分解技术，有

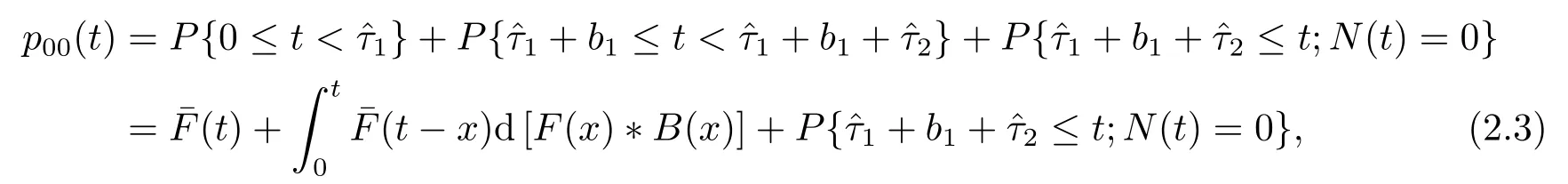
上式第三项实际上可以分成延迟期有顾客到达和无顾客到达两种情况:

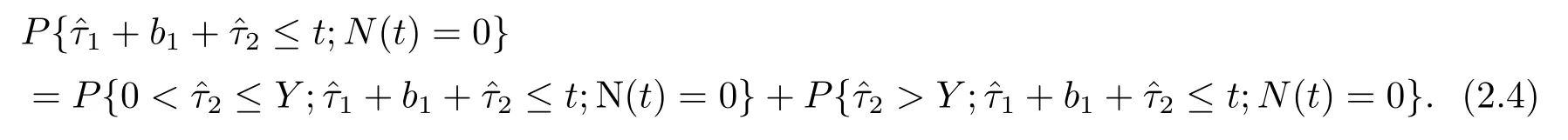
1) (2.4)式中第一项就为延迟期有顾客到达，则到达一个顾客后服务员就立即结束延迟期进入忙期为顾客服务，如图2.1所示

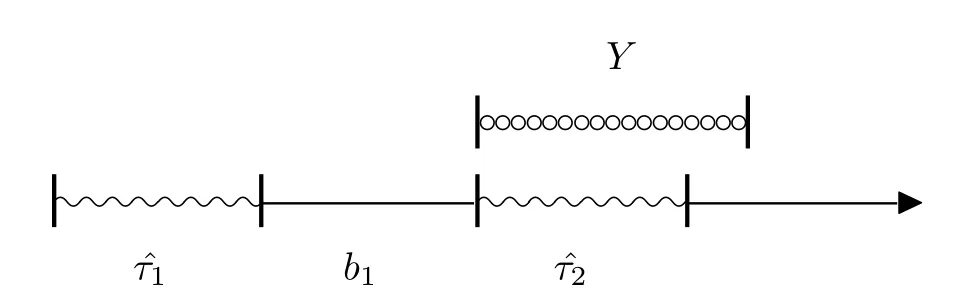
图2.1

则按图2.1所示进行分解为

2) (2.4)式中第二项为延迟期无顾客到达，延迟期结束以后服务员立刻休假，如图2.2所示

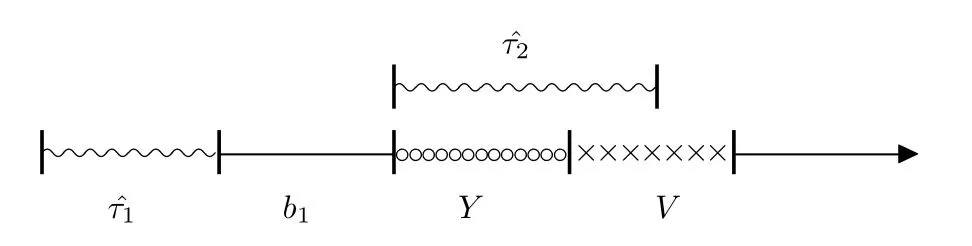
图2.2

① 假期到达人数不足N个，即休假期中到达n(0 ≤n ≤N -1)个，则服务员休假转来处于待岗状态，直到后面再到达N -n个，才开始为顾客服务.假期无顾客到达与休假期到达n(0 ＜n ≤N -1)个分别如图2.3，图2.4所示

图2.3

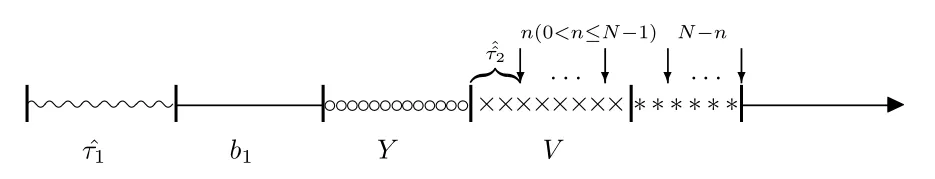
图2.4

② 假期到达人数大于等于N个，即服务员休假转来之后发现系统中顾客人数为n(n ≥N)个，则立即为顾客服务，如图2.5所示

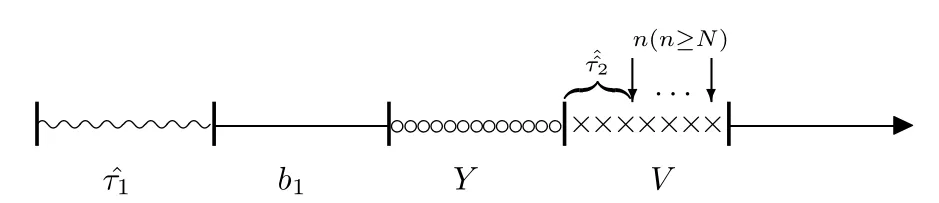
图2.5

于是

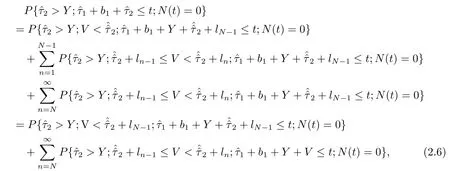
(2.6)式中第一项为

(2.6)式中第二项为

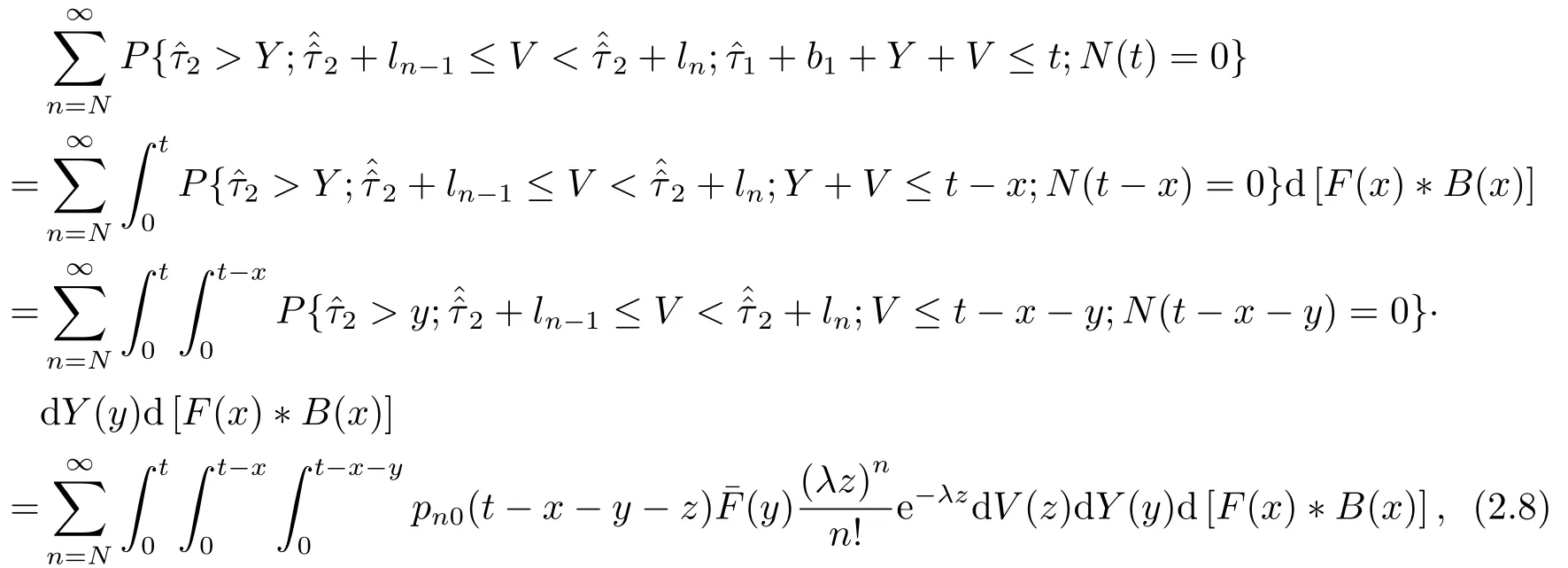
将(2.4)-(2.8)式代入(2.3)式整理得到

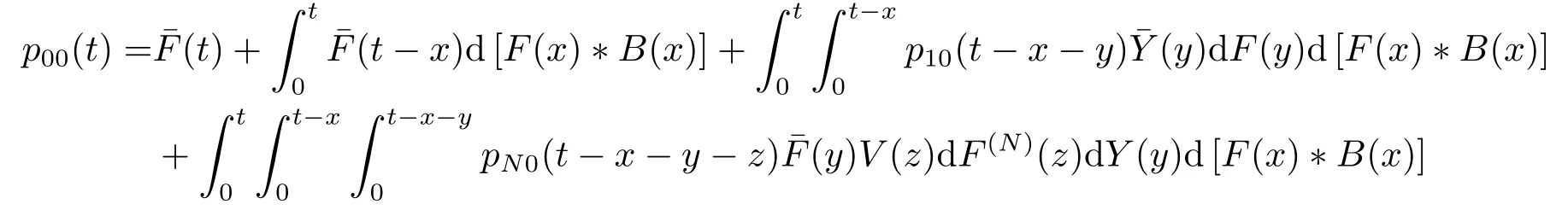
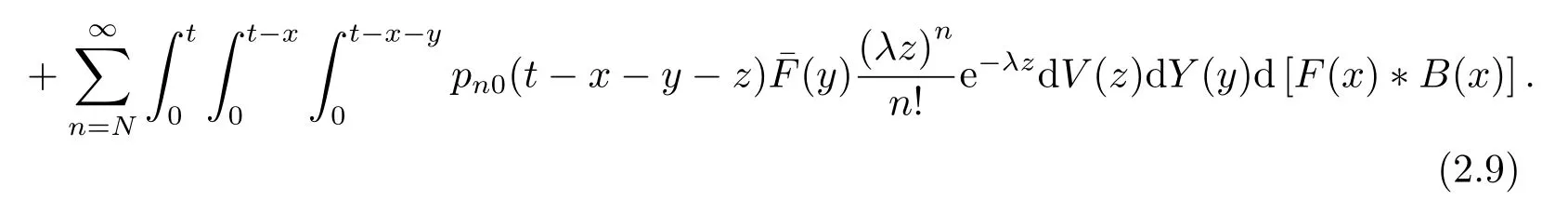
同理，对i ≥1，有

对(2.9)-(2.10)式作L变换，得

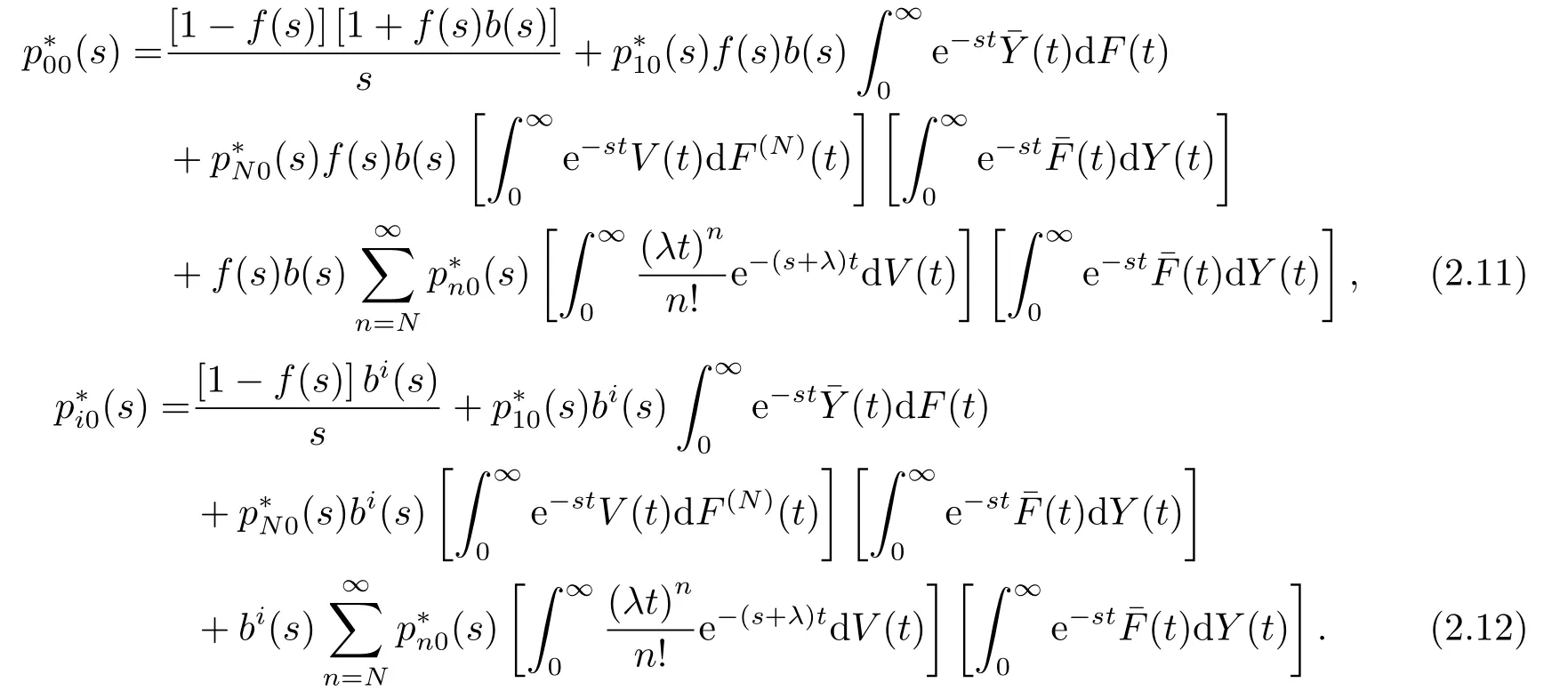
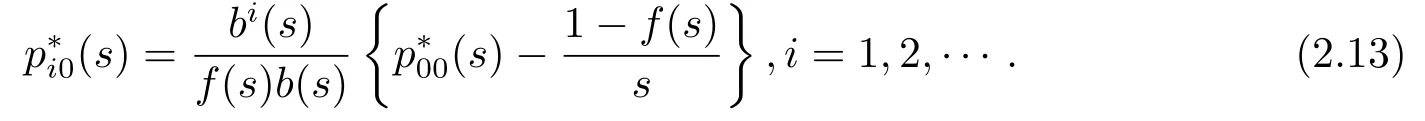
再将(2.13)代入(2.11)式，经过整理可得到(2.1)式，再把(2.1)代入(2.13)式可得(2.2)式，证毕.

定理2.2对ℜ(s)＞0和i ≥1，有

1) 当j =1，2，···N -1时，

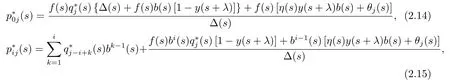
2) 当j ≥N时，

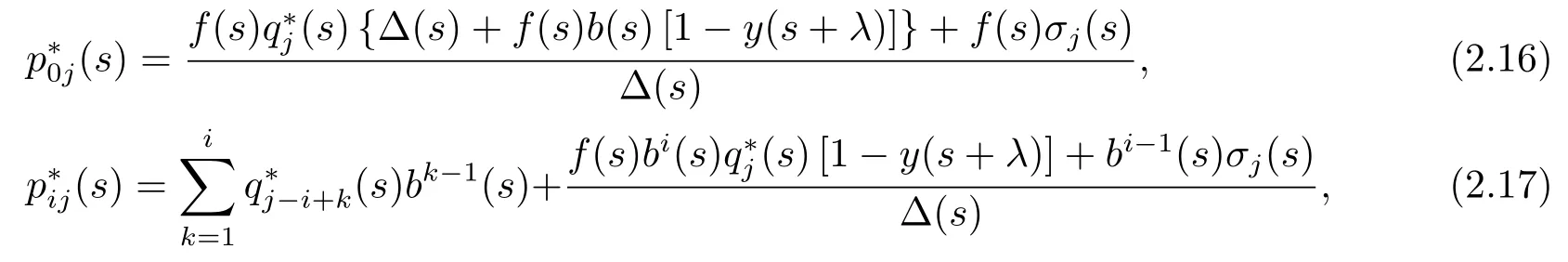
其中

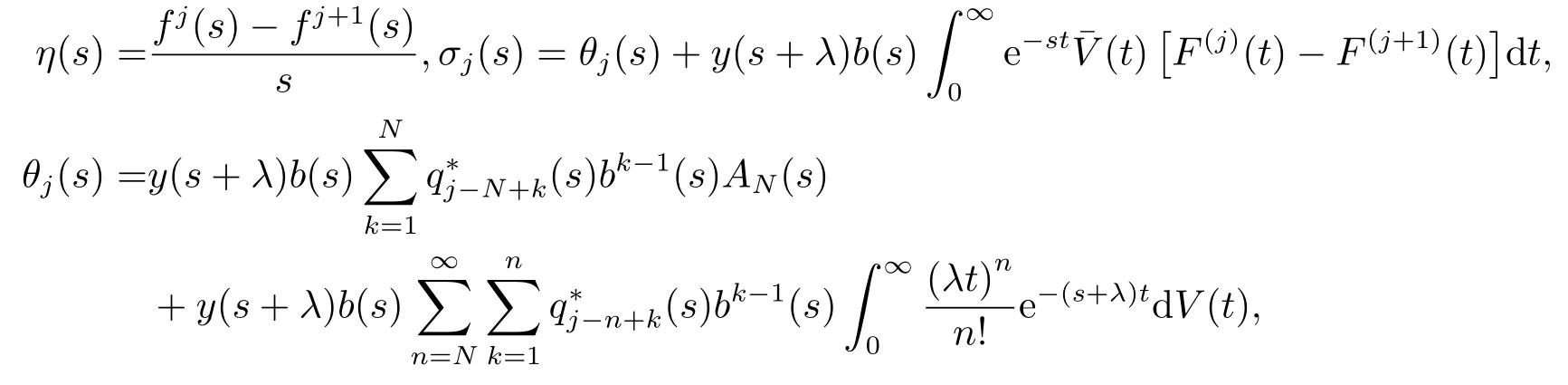
Δ(s)，AN(s)如定理2.1所述.

证当j = 1，2，··· ，N -1时，“时刻t队长为j”当且仅当“时刻t落在服务员假期中且队长为j”或者“时刻t落在服务员忙期中且队长为j”，类似定理2.1的分解，得

(2.18)式中的第一项表示时刻t处于第一个服务员忙期中且队长为j的概率，第二项表示在延迟期中有顾客到达时，时刻t处于第一个服务员忙期之后且队长为j的概率.

当延迟期无顾客到达时服务员就立刻休假，(2.18)式中的第三项表示无论假期中到达多少个顾客，时刻t处于下一个服务员忙期之前且队长为j的概率，如图2.6(时刻t 处于假期中)，图2.7(时刻t处于假期结束后的服务员闲期中)所示.

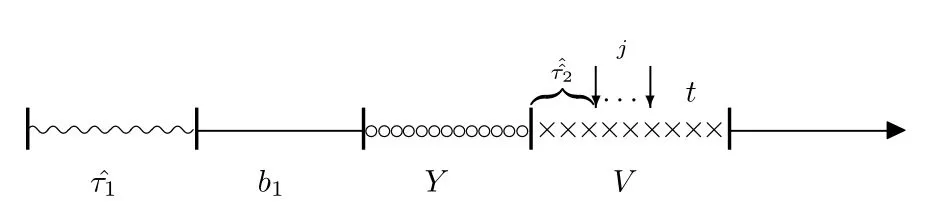
图2.6

图2.7

进一步(2.18)式中的第三项为

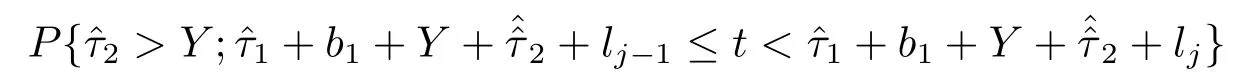
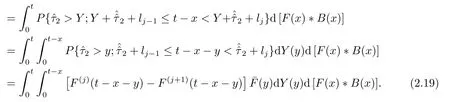
第四项表示假期到达n(0 ≤n ≤N -1)个顾客，t落在下一个“服务员忙期”开始之后且队长为j的概率，如图2.8(假期中无顾客到达)，图2.9(假期中到达n(0 ＜n ≤N -1)个)所示.

图2.8

图2.9

则

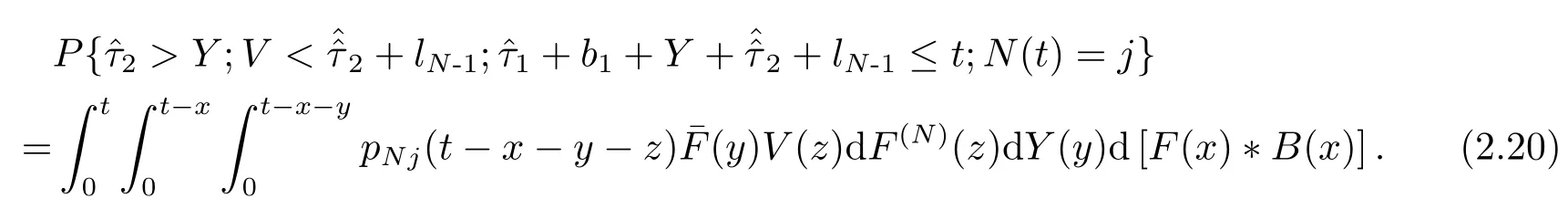
第五项表示假期中到达n(n ≥N)个顾客，t落在下一个“服务员忙期”开始之后且队长为j的概率，如图2.10所示.

我说：“这下你知道孩子为什么磨蹭了吧？”她很惊讶地说：“难道是因为我吗？不会吧！我每天都在催他做事情呀！我对他要求很严的！我现在之所以觉得应该找点事情做，是不想让我儿子看不起我！”

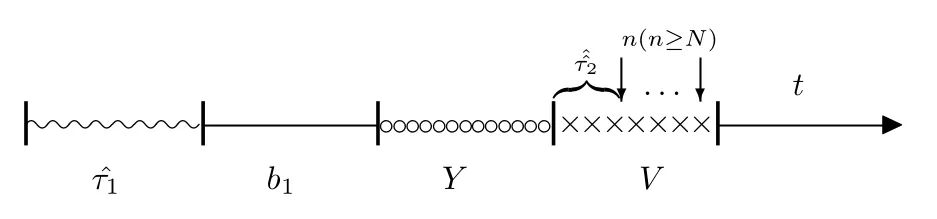
图2.10

则

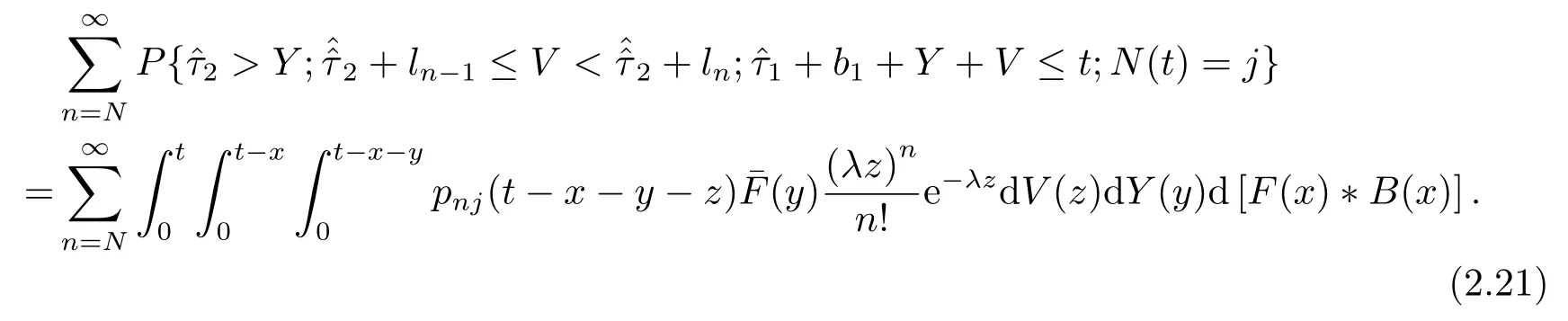
将(2.19)-(2.21)式代入(2.18)式整理得

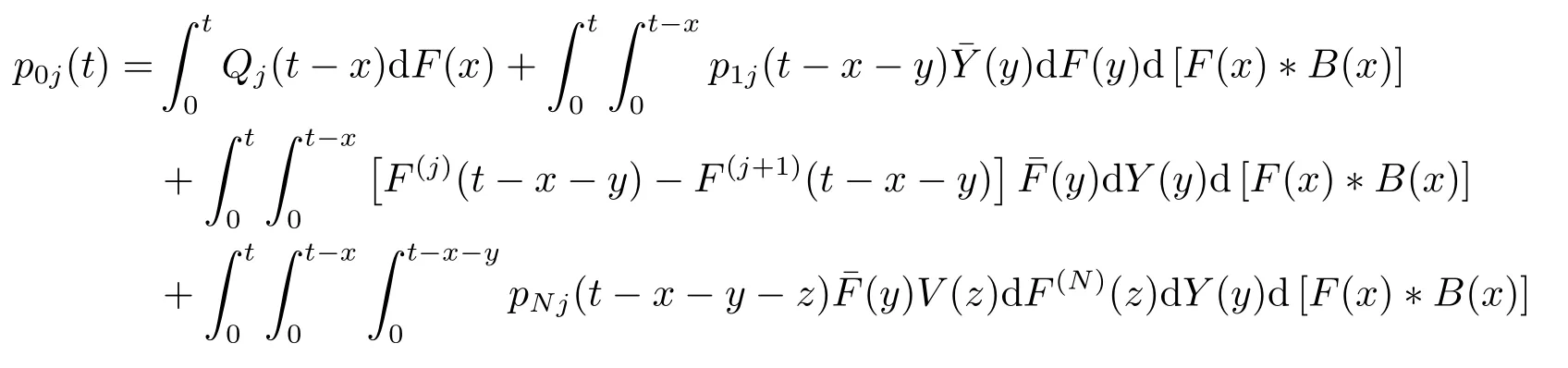
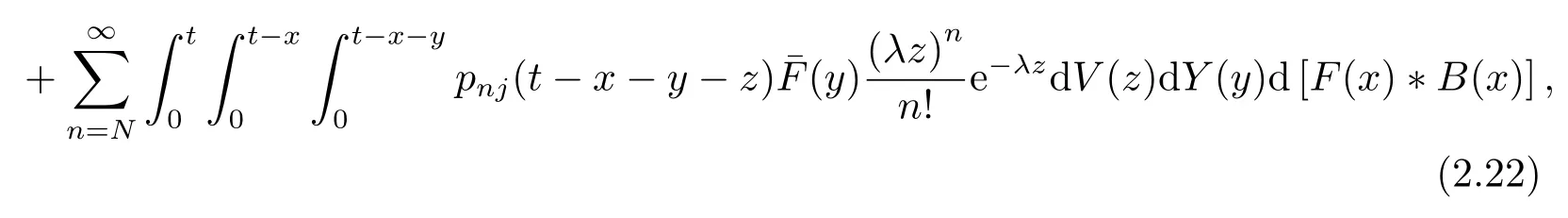
同理

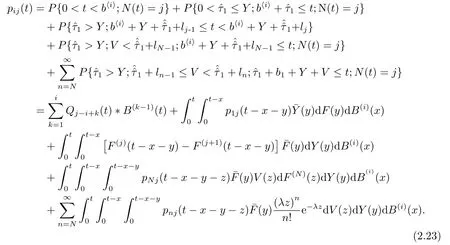
对(2.22)-(2.23)式作L变换，得

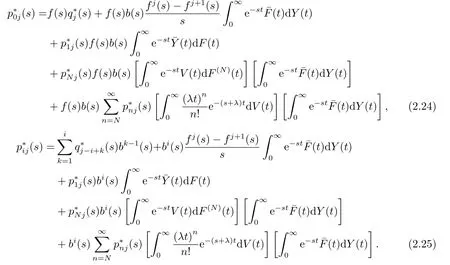
由(2.24)-(2.25)式得到p0j(s)，pij(s)的关系式为

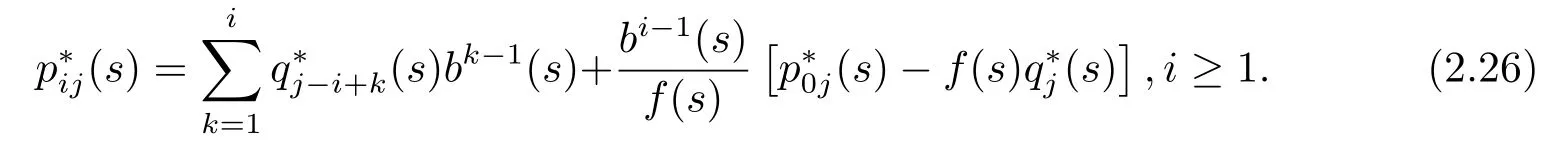
再将(2.26)式代入(2.24)式，经过整理化简可得到(2.14)式，再将(2.14)式代入(2.26)式，得证(2.15)式.

当j ≥N时，“时刻t队长为j”当且仅当“时刻t落在服务员假期中且队长为j”或者“时刻t落在服务员忙期中且队长为j”，同理得

余下证明过程类似1 ≤j ＜N时的推导过程，证毕.

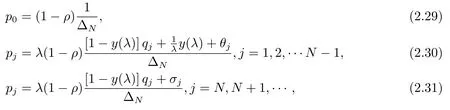
此时{pj，j =0，1，2，···}构成概率分布，其中

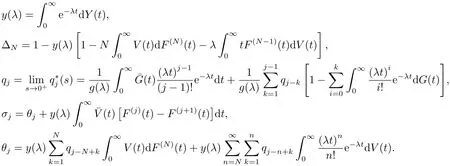
证由下面求事实上，当＞1或ρ =注意到此时或且E(b) = ∞以及与当E(b)=∞，有

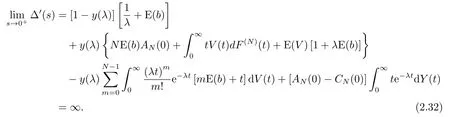
再将(2.34)-(2.35)式代入(2.33)式中，即可完成证明.

定理2.4令P延迟-Min(N，V)(z)表示该系统稳态队长分布的概率母函数，则当ρ ＜1时，有

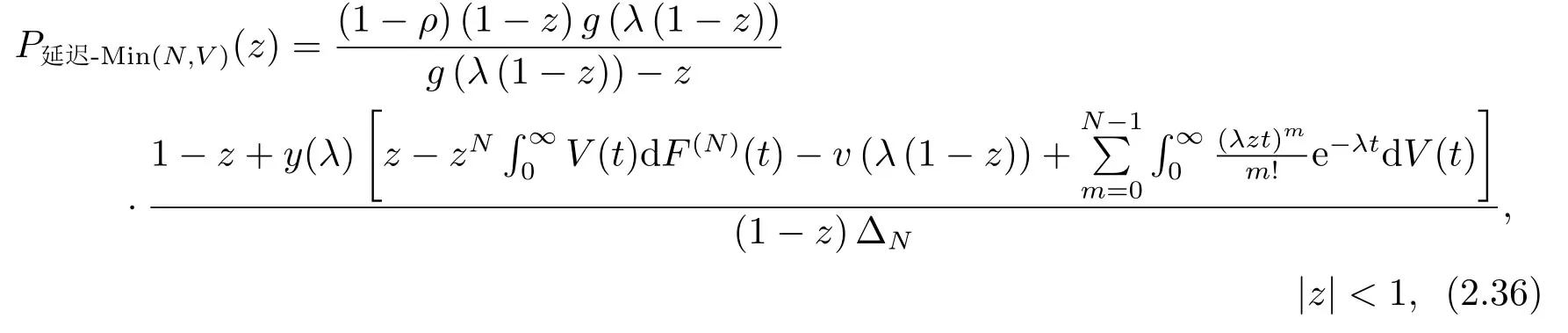
而且平均队长为

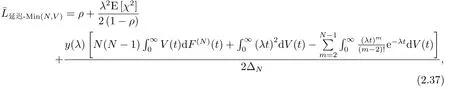
证由可得

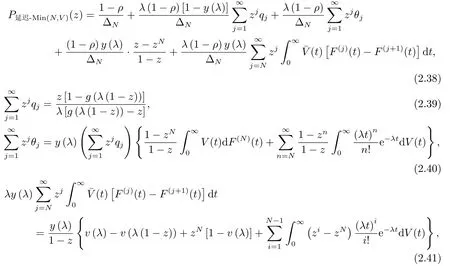
将(2.39)-(2.41)式代入(2.38)式整理得(2.36)式，再由经过计算即得(2.37)式.

定理2.5本文研究的具有N-策略和延迟单重休假且休假不中断的M/G/1排队系统的稳态队长可以分解成独立的两部分之和: 一部分是经典排队系统的稳态队长，一部分是由N-策略延迟单重休假且休假不中断的策略机制引起的附加队长Ld，且附加队长Ld有如下离散分布

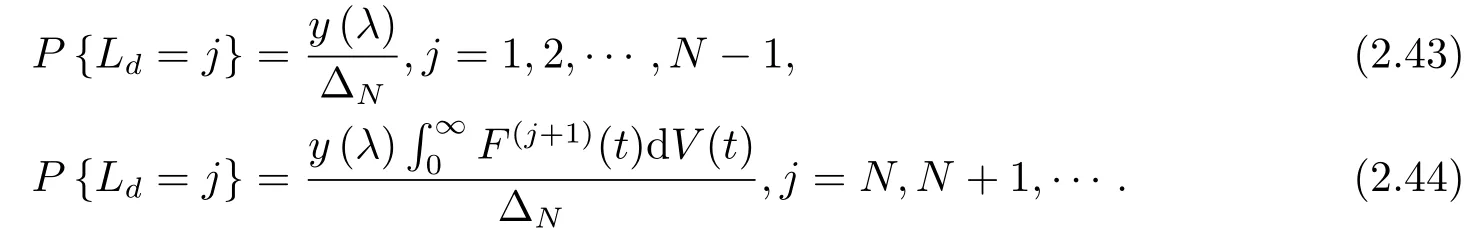
证由上面定理2.4可知本文研究的排队系统的稳态队长可分解成独立的两部分之和，下面证明附加队长有上式的离散分布，令

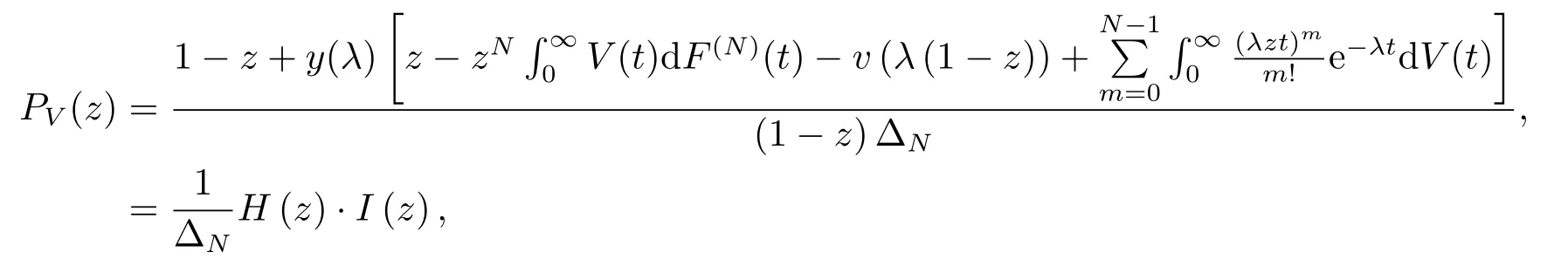
其中

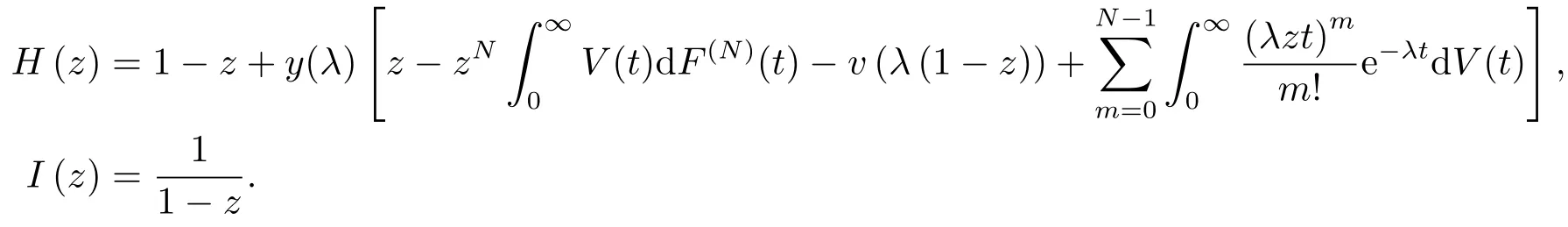
推论2.1当P {Y =0} = 1时，本文研究的系统就成为了N-策略单重休假且休假不中断的M/G/1排队系统，即文[8]中研究的系统，在上述所有结论中由y(λ)=1，有

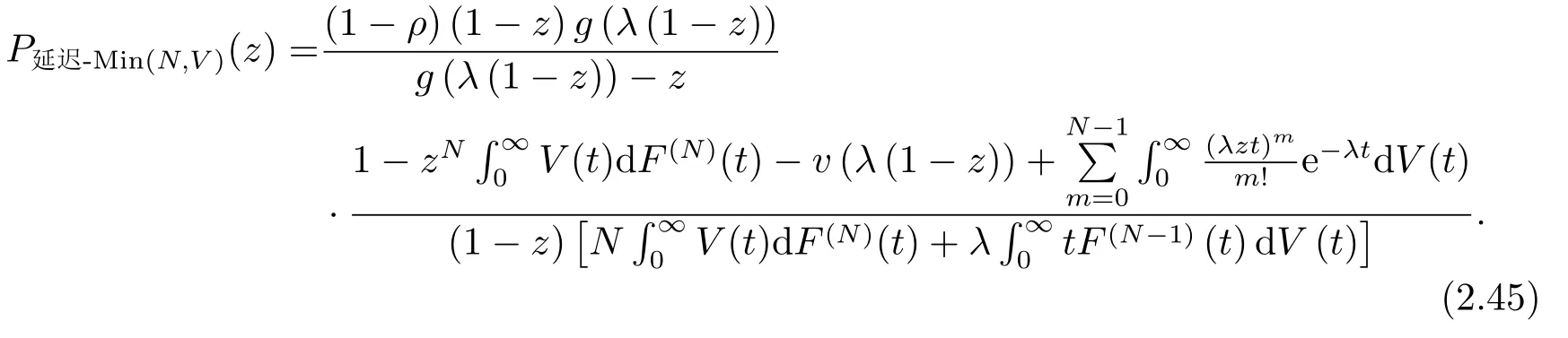
注2.2文[8]的母函数有误，文[8]的母函数为

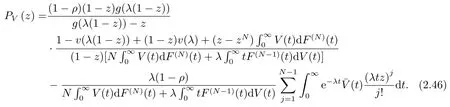
当z =1时，

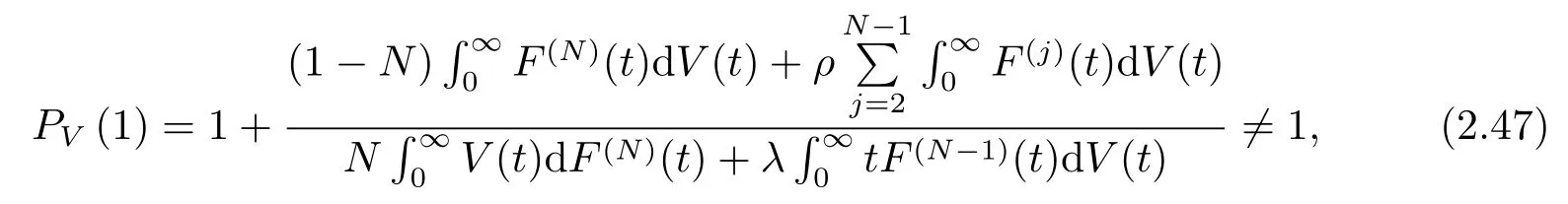
文[8]的正确的母函数即为(2.45)式.

推论2.2当P {Y =∞} = 1时，本文研究的系统就成为了经典的M/G/1排队系统，在上述所有结论中令y(λ)=0即得到与文[6]完全一致的结论.

推论2.3当P {V =0}=1，本文研究的系统就成为了延迟N-策略M/G/1排队系统，在上述所有结论中令V (t)=1，v(λ(1-z))=1，即得到与文[7]完全一致的结论.

3.费用模型下的最优控制策略

建立如下的费用模型

1) R: 系统(服务台)在一个更新周期内的固定消耗(或系统启动)费用;

2) h: 一个顾客在系统中逗留(包括等待和服务)单位时间的成本费用.

记FN为延迟单重休假且休假不中断和N-策略的控制机制下系统长期运行单位时间内所产生的成本期望费用.由更新报酬过程理论知

服务员忙期的平均长度为

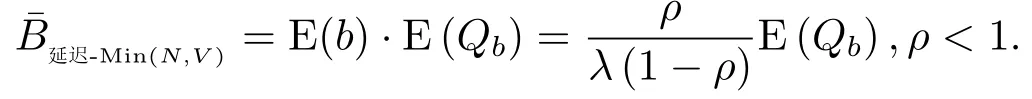
由于服务员忙期开始时在系统内的顾客数为上一个“服务员非忙期”内到达的顾客数，而顾客到达过程是参数λ的泊松过程，因此“服务员非忙期”的平均长度为

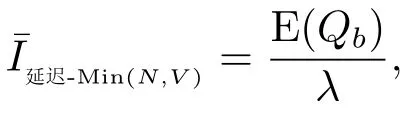
故系统一个更新周期(由一个“服务员忙期”和一个“服务员非忙期”构成)的平均长度为

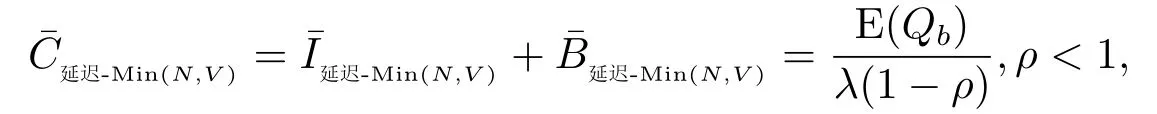
于是，系统长期运行单位时间内所产生的成本期望费用为

下面计算服务员忙期开始时系统中的平均顾客数E(Qb).而Qb的分布，经计算，可得

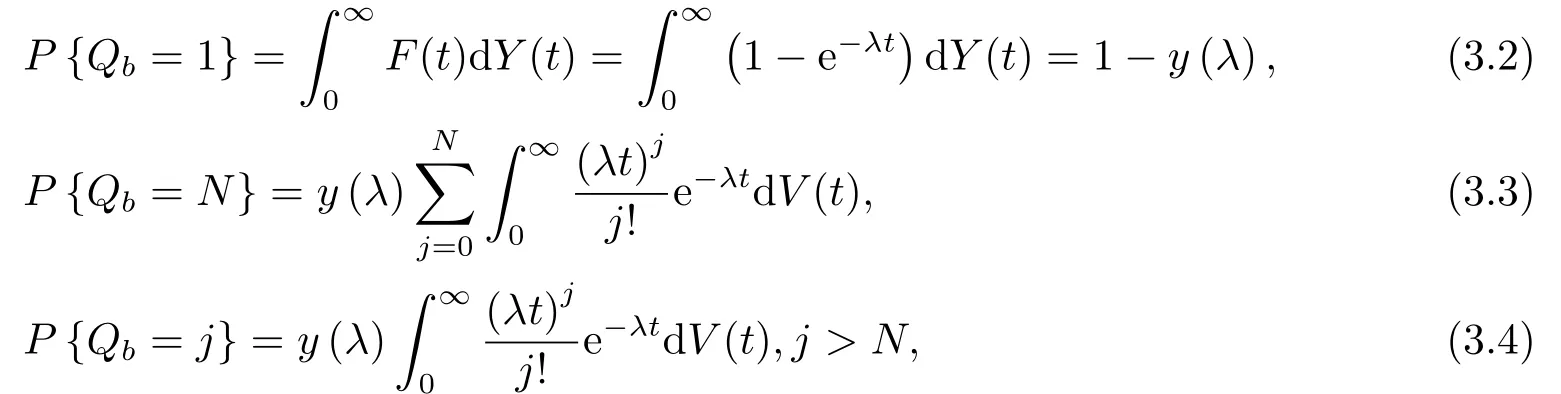
于是

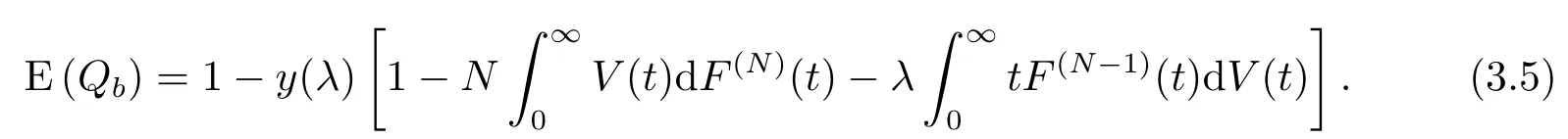
将(2.37)，(3.5)式代入(3.1)式得

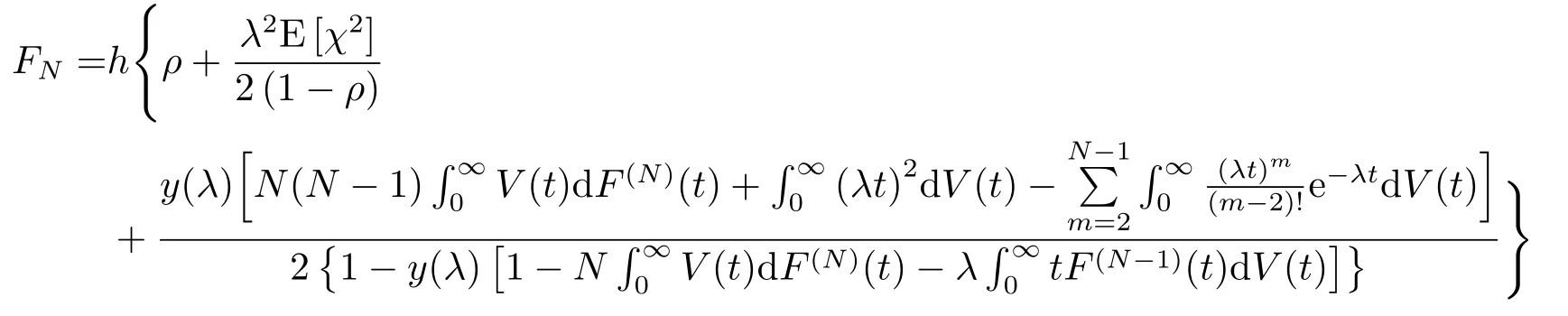
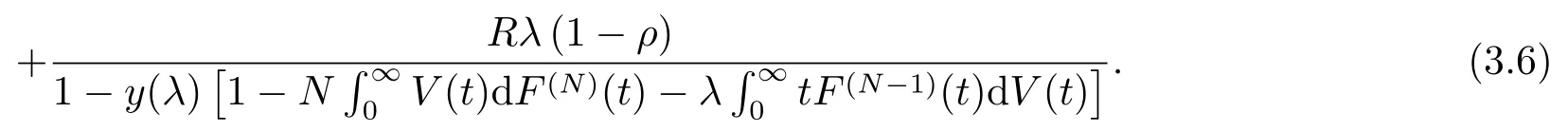
实例取服务时间χ的分布G(t) = 1-e-µt，延迟期Y 的分布Y (t) = 1-e-αt，t ≥0，休假时间V 的分布V (t)=1-e-θt，则

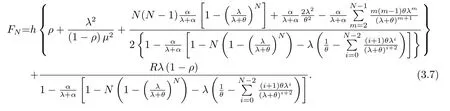
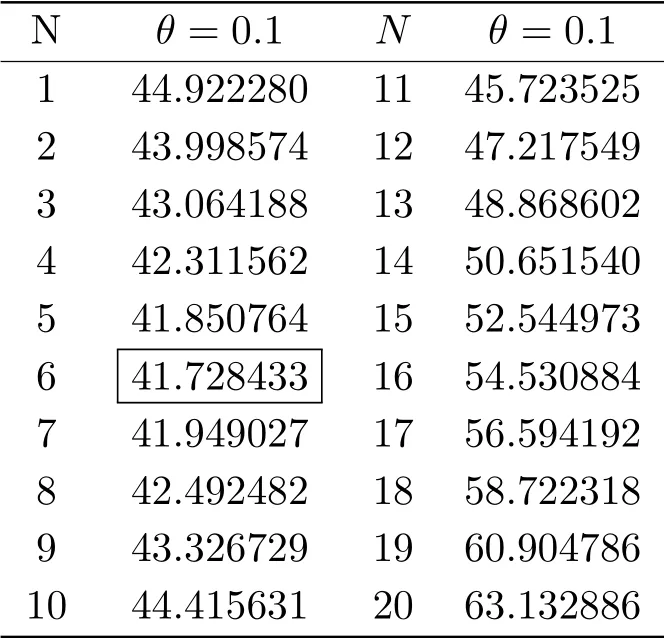
表3.1 取R=100，h=5，λ=0.6，µ=0.8，ρ=0.75，α=0.8，θ =0.1，FN随N的变化

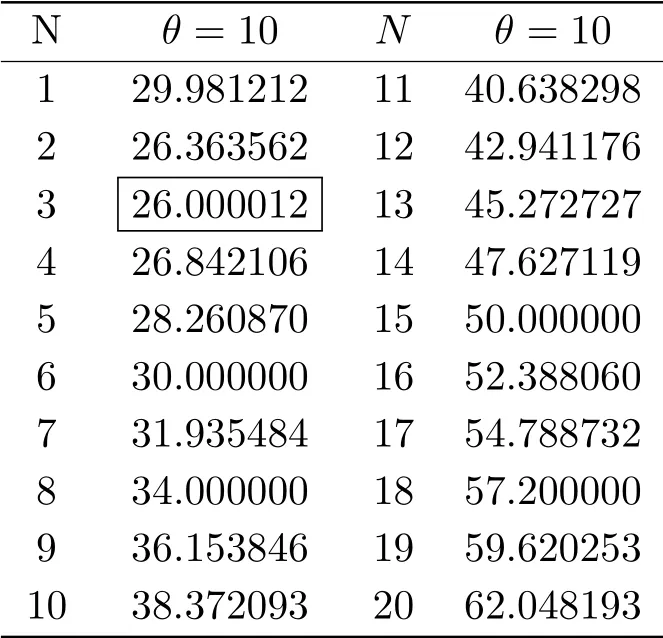
表3.2 取R=100，h=5，λ=0.6，µ=0.8，ρ=0.75，α=0.8，θ =10，FN随N的变化

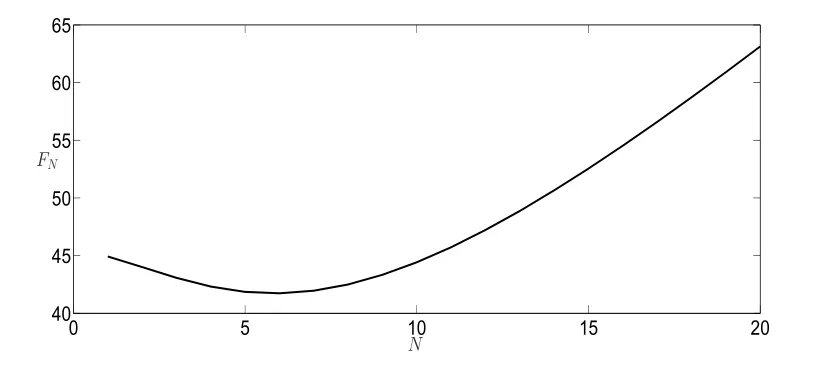
图3.1 取R=100，h=5，λ=0.6，µ=0.8，ρ=0.75，α=0.8，θ =0.1，FN随N的变化

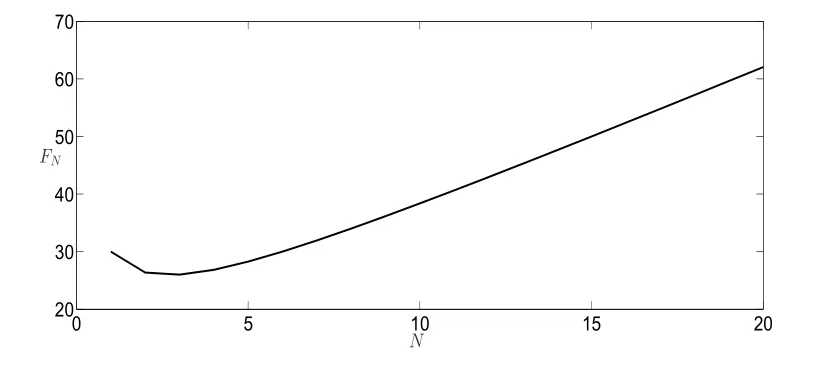
图3.2 取R=100，h=5，λ=0.6，µ=0.8，ρ=0.75，α=0.8，θ =10，FN随N的变化

从表3.1，表3.2，图3.1和图3.2上看出，当休假时间V 参数θ固定时，随着N的增大，FN呈现先减小后增大的趋势，θ =0.1时，在N =6的时候FN取得最小值41.728433; θ =10时，在N =3的时候FN取得最小值26.000012.