A New Iteration Method for M-matrix Algebraic Riccati Equations

GUAN Jinrui(关晋瑞)，REN Fujiao(任孚鲛)，SHAO Rongxia(邵荣侠)

(1.Department of Mathematics，Taiyuan Normal University，Jinzhong 030619，China;2.School of Statistics and Data Science，Xinjiang University of Finance and Economics，Urumqi 830012，China)

Abstract:In this paper，we consider numerical solution of the M-matrix algebraic Riccati equation(MARE).We propose a new iteration method for computing the minimal nonnegative solution of the MARE，which is obtained by transforming the MARE to its discrete form.Convergence of the new iteration method is proved by choosing proper parameters for the MARE.Theoretical analysis and numerical experiments are given to show that the new iteration method is feasible and is effective than some existing methods under certain conditions.

Key words:Algebraic Riccati equation;M-matrix;Minimal nonnegative solution;Newton method;ALI iteration method

1.Introduction

In this paper，we consider numerical solution of the nonsymmetric algebraic Riccati equation

whereA，B，C，Dare real matrices of sizesm×m，m×n，n×m，n×nrespectively，and

is an M-matrix.This class of nonsymmetric algebraic Riccati equation is called M-matrix algebraic Riccati equation(MARE).

The MARE has wide applications in many branches of applied mathematics，such as applied statistics，transportation theory，optimal control，and so on[2，4-5，9，11].The MARE has been studied extensively in recent years.See[1，4-5，7-10，12]and the references therein for an incomplete references.

In the following，we review some definitions and basic results of M-matrix，which are needed in the sequel.

For any matricesA=(aij)，B=(bij)∈Rm×n，we writeA≥B(A＞B)，ifaij≥bij(aij＞bij)for alli，j.A matrixAis called a Z-matrix ifaij≤0 for all.A Z-matrixAis called an M-matrix if there exists a nonnegative matrixBsuch thatA=sI-Bands≥ρ(B)whereρ(B)is the spectral radius ofB.In particular，Ais called a nonsingular M-matrix ifs＞ρ(B)and singular M-matrix ifs=ρ(B).

Lemma 1.1[3]LetAbe a Z-matrix.Then the following statements are equivalent:

1)Ais a nonsingular M-matrix;

2)A－1≥0;

3)Av＞0 for some vectorsv＞0;

4)All eigenvalues ofAhave positive real part.

Lemma 1.2[3]LetAandBbe Z-matrices.IfAis a nonsingular M-matrix andA≤B，thenBis also a nonsingular M-matrix.In particular，for any nonnegative real numberα，B=αI+Ais a nonsingular M-matrix.

Lemma 1.3[3]LetAbe a nonsingular M-matrix or an irreducible singular M-matrix.LetAbe partitioned as

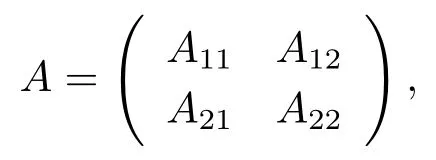
whereA11andA22are square matrices.ThenA11andA22are nonsingular M-matrices.

The solution for(1.1)of practical interest is the minimal nonnegative solution.It is shown in[5-6]that equation(1.1)has a unique minimal nonnegative solution，which is of practical interest.

Lemma 1.4[5－6]IfKis a nonsingular M-matrix or an irreducible singular M-matrix，then(1.1)has a unique minimal nonnegative solutionS.IfKis nonsingular，thenA-SCandD-CSare also nonsingular M-matrices.IfKis irreducible，thenS＞0 andA-SCandD-CSare also irreducible M-matrices.

The rest of the paper is organized as follows.In Section 2，we review some efficient numerical methods for solving the MARE.In Section 3，we first propose a new iteration method for computing the minimal nonnegative solution of MARE and then give convergence analysis of it.In Section 4，we use some numerical examples to show the feasibility and effectiveness of the new iteration method.Conclusions is given in Section 5.

2.Some Existing Numerical Methods

In this section，we review some existing numerical methods for solving the MARE.

Recently，many numerical methods have been proposed for solving the MARE，such as Schur method，fixed-point iteration methods，Newton method，ALI iteration method，SDA，and so on.

In[5，7]，GUO et al.proposed the Newton method for solving the MARE as follows:

Convergence analysis in[7]showed that the Newton method is quadratically convergent for the noncritical case，and is linearly convergent for the critical case.However，since at each iteration a Sylvester matrix equation is required to solve，the Newton method is very expensive.

In[5，12]，some fixed-point iteration methods were proposed for solving the MARE.The general form of the fixed-point iteration methods is as follows:

whereA=A1-A2，D=D1-D2are given splittings ofAandD.Some choices of splitting are given in the following:

Though the fixed-point iteration methods are easy to implement，they may require a large number of iterations to converge.Convergence analysis in[5]showed that the fixed-point iteration methods have linear convergence rate for the noncritical case and have sublinear convergence rate for the critical case.

In[1]，BAI et al.proposed the ALI iteration method for solving the MARE as follows:

whereX0=0 andα＞0 is a given parameter.Since at each iteration only two linear matrix equations are needed to solve，the ALI iteration method is much cheaper than Newton method.Convergence analysis showed that the ALI iteration method is linearly convergent for the noncritical case and is sub-linearly convergent for the critical case.

For other efficient numerical methods，we refer to[4，8，12]for an incomplete references.

3.A New Iteration Method

In this section，we propose a new iteration method for solving the MARE，and then give convergence analysis of it.

First，write the equation(1.1)as the form

By choosingα＞0，β＞0，the equation(3.1)can be written as

Making use of generalized Cayley transform and multiplying both sides by(βI+A-XC)－1，(αI+D-CX)－1respectively，we can transform it into the following discrete form

Letting

and noting that

we have

Thus we get the iteration as follows:

where

A new iteration method(NI):

i)SetX0=0∈Rm×n;

ii)Fork=0，1，···，until{Xk}converges，computeXk+1fromXkby

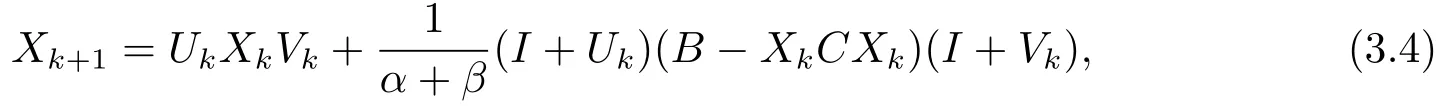
whereUk，Vkare defined as in(3.2)-(3.3)andα＞0，β＞0 are two given parameters.

Compared with the methods in Section 2，the new iteration method is feasible，since at each iteration only two matrix inverses and matrix multiplications are needed to compute.Hence less CPU time are required for solving the MARE.

In the following，we give convergence analysis of the new iteration method.We first need two lemmas.

Lemma 3.1For the MARE(1.1)，ifKin(1.2)is a nonsingular M-matrix or an irreducible singular M-matrix and the parametersα，βsatisfy

then the sequence{Xk}generated by(3.4)is well defined and satisfies

ProofWe prove(3.6)by induction.Whenk=0，it is clear that 0=X0≤S.Thus，(3.6)holds true fork=0.

Suppose that(3.6)holds true fork=l.Then we have

SinceA-SCis an M-matrix and 0≤Xl≤S，we knowA-XlCis an M-matrix.By Lemma 1.2，βI+A-XlCis a nonsingular M-matrix.Similarly，αI+D-CXlis also a nonsingular M-matrix.Thus，from Lemma 1.1，we have(βI+A-XlC)－1≥0 and(αI+D-CXl)－1≥0.Hence，we haveXl+1-S≤0 and(3.6)holds true fork=l+1.

By induction，(3.6)holds true for allk≥0.

Lemma 3.2Under the assumptions in Lemma 3.1，the sequence{Xk}generated by(3.4)satisfies

ProofWe prove(3.7)by induction.Whenk=0，we have

SinceKin(1.2)is a nonsingular M-matrix or an irreducible singular M-matrix，AandDare nonsingular M-matrices by Lemma 1.3.Thus，βI+AandαI+Dare are nonsingular M-matrices by Lemma 1.2.Thus we haveU0≥0，V0≥0，and

Hence，(3.7)holds true fork=0.

Suppose that(3.7)holds true fork=l.We have

From Lemma 3.1，we know bothβI+A-XlCandαI+D-CXlare nonsingular M-matrices.By Lemma 1.1，we have(βI+A-XlC)－1≥0 and(αI+D-CXl)－1≥0.ThusXl+1-Xl≥0 and(3.7)holds true fork=l+1.

By induction，(3.7)holds true for allk≥0.

Using the two lemmas above，we can prove the convergence of the new iteration method.

Theorem 3.1For the MARE(1.1)，ifKin(1.2)is a nonsingular M-matrix or an irreducible singular M-matrix and the parametersα，βsatisfy(3.5)，then the sequence{Xk}generated by the new iteration method(3.4)is well defined，monotonically increasing，and converges to the minimal nonnegative solutionS.

ProofWe have shown in Lemma 3.1 and Lemma 3.2 that{Xk}is nonnegative，monotonically increasing and is bounded from above.Thus there is a nonnegative matrixS*such thatFrom Lemma 3.1，we haveS*≤S.On the other hand，taking limit in(3.4)，we knowS*is a solution of equation(1.1).Thus，by Lemma 1.4 we knowS≤S*.HenceS=S*.

4.Numerical Experiments

In this section we use several examples to show the feasibility and effectiveness of the new iteration method(NI).We compare NI with Newton method(Newton)in[5，7]，fixed-point iteration method(FP3)in[5]，ALI iteration method(ALI)in[1]，and present computational results in terms of the numbers of iterations(IT)，CPU time(CPU)in seconds and the residue(RES)，where

In our implementations all iterations are performed in MATLAB(version R2012a)on a personal computer with 2G CPU and 8G memory，and are terminated when the current iterate satisfiesRES＜10－6.In the experiments，the parameters in the NI method are chosen to beα=max{aii}，β=max{djj}.

Example 4.1Consider the MARE(1.1)with

whereEm×nis them×nmatrix with all ones andImis the identity matrix of sizemwithm=2，n=18.This example is from[4]where the correspondingMis an irreducible singular M-matrix.The numerical results are summarized in Tab.4.1.

Tab.4.1 Numerical results of Example 4.1

For this example，the ALI iteration method can not converge in 9000 iterations，while the other three methods perform very well.

Example 4.2Consider the MARE(1.1)with

This example is from[12]，where the correspondingKis an irreducible singular M-matrix.For different sizes ofn，the numerical results are summarized in Tab.4.2.

Tab.4.2 Numerical results of Example 4.2

For this example，all the four methods perform very well，while NI needs the least CPU time.

Example 4.3Consider the MARE(1.1)for which

andB=SD+AS-SCSsuch that

is the minimal nonnegative solutionn of(1.1)，where

andn=m2.This example is taken from[1].For different sizes ofm，the numerical results are summarized in Tab.4.3.

Tab.4.3 Numerical results of Example 4.3

For this example，all the four methods perform very well，while FP3 is the most expensive one.

From the three experiments，we can conclude that NI is feasible，and in some cases it is effective than other methods.

5.Conclusions

We have proposed a new iteration method for computing the the minimal nonnegative solution of MARE.Convergence of the new method is proved for the MARE associated with a nonsingular M-matrix or an irreducible singular M-matrix.Numerical experiments have shown that the new iteration method is feasible and is efficient in some cases.However，for the critical case，the new iteration method may be very slowly.So in this case the SDA will be more preferable.