尹琳琳
特殊发现:理解透彻打基础
尹琳琳
课本的例题和习题中有不少问题可以通过增加、变换情境,改变设问方式,将一般性问题改为拓展迁移型问题.该类型试题通过提供一段文字、素材或图表材料,来展示一个数学要领、结论的形成和应用过程,或一个新数学公式的推导和应用,或介绍一种解题方法等.近年来,此类题在中考试卷中频频出现,值得关注.
(2015·莆田)在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:把图1中的△AEF绕着点A顺时针旋转.
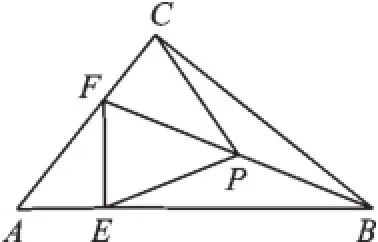
图1
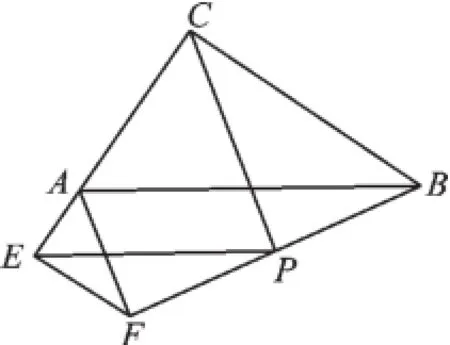
图2
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由.
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
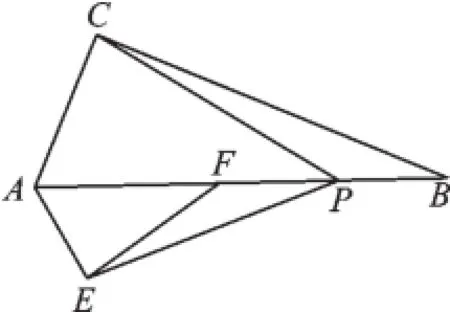
图3
【思路突破】本题的“特殊发现”虽然不要求证明,但必须理解透彻.这一步是利用直角三角形斜边上的中线等于斜边的一半这一定理.这个问题中所涉及的证明思路和基本图形将为下面问题的解决打下基础.
问题探究(1)通过作辅助线构造全等三角形,得对应边相等,从而可以出现直角三角形斜边上中线这一基本图形,得到结论.
问题探究(2)以问题探究(1)的解题思路为背景,同样通过作辅助线得直角三角形,利用斜边中线性质解题,只是解决这个问题时说明所构造的三角形是直角三角形是难点,需要利用两步全等给予解决.注意∠EAF=∠CAB是隐含条件.
问题探究(3)从△CPE是等边三角形入手,结合圆周角定理得到k的值.
解:(1)PC=PE成立,理由如下:
如图4,延长CP交EF的延长线于点M,
∵∠ACB=∠AEF=90°,
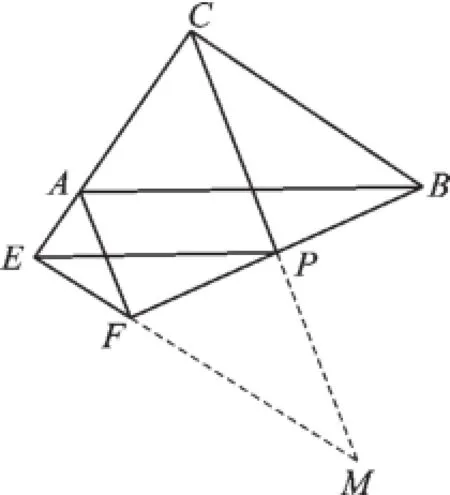
图4
∴BC∥EF,
∴∠BCP=∠M,
又∵∠BPC=∠FPM,PF=PB,
∴△CPB≌△MPF,
∴PC=PM,
利用直角三角形斜边中线性质,
得:PC=PE.
(2)PC=PE成立,理由如下:
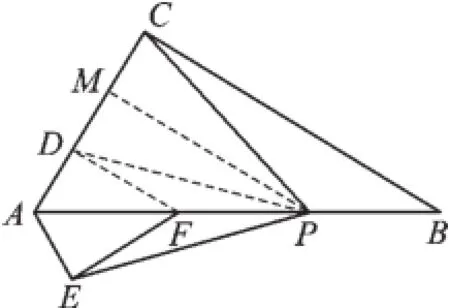
图5
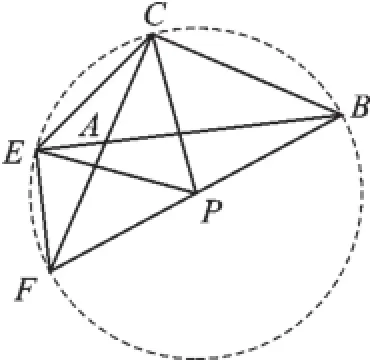
图6
如图5,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD.
易得:∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,

∴△DAP≌△EAP(SAS),
∴PD=PE.
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
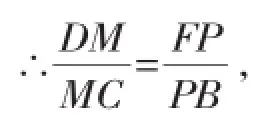
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,∴PC=PD,
又∵PD=PE,∴PC=PE.
(3)∵△CPE是等边三角形,
∴由旋转的性质得,△AEF绕着点A顺时针旋转180°后,△CPE仍是等边三角形,
∵∠BCF=∠BEF=90°,点P是BF的中点,
∴点C、E在以点P为圆心,BF为直径的圆上,
∵△CPE总是等边三角形,
∴∠CPE=60°,
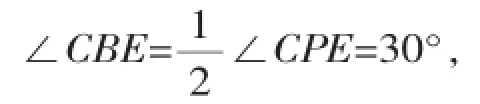
即∠ABC=30°,
在Rt△ABC中,
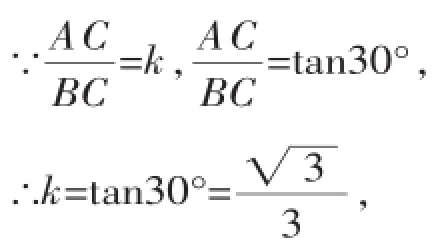
【解后反思】该试题设计的3个问题由浅入深,特殊发现给我们暗示了探究的方向和解题方法,问题(1)(2)是以特殊发现为基础,在改变点E、F位置的过程中,图形的形状虽然发生了变化,但解决问题的方法不变,△CPB和△MPF的全等关系不变,即问题的本质不变.想方设法寻找旋转过程中的“变”与“不变”,其核心是找到“变”中的“不变”,解题的关键是抓住题目中的“题根”,联想基本图形,寻找解题的多种策略.
(作者单位:江苏省丰县初级中学)



