贲道波
“图形的变化”是初中数学的核心知识,也是中考的重要内容,主要包括图形的平移、翻折、旋转、相似和投影.现以一道课本习题为出发点,谈谈它的变式,希望对大家的学习有所启发.
【原题】(苏科版《数学》九下第90页第11题)如图1,△ABC和△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别交AD、AE于点F、G.图中有哪几对相似三角形(不包括全等)?把它们表示出来,并说明理由.
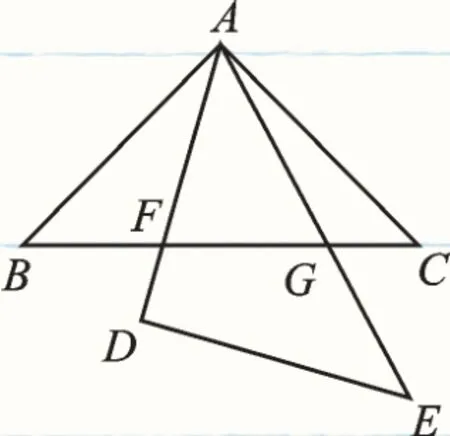
图1
【解析】由∠B=∠FAG=∠C=45°,∠BGA=∠AGF,∠AFG=∠CFA,可证得△AGF∽△BGA∽△CAF.
一、对原题的分析
【编写意图】本题用两个等腰直角三角形进行组合,复习巩固三角形相似判定方法——“两组角分别相等的两个三角形相似”(本文以下简称“两角法”).
【图形分解】本题从图1中可分解出图2、图3两组三角形相似的基本图形——“共角共边型”.
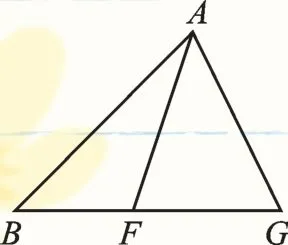
图2
结论延伸:①在图2中,由“共边型”相似:△GAF∽△GBA,易得GA2=GF·GB,反之亦成立.
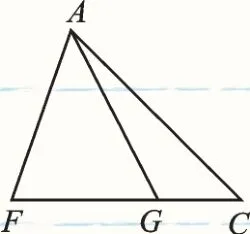
图3
②如图4,若把图2中的AF平移并缩小至A′F′,可得“共角型”相似:△GA′F′∽△GAF∽△GBA.
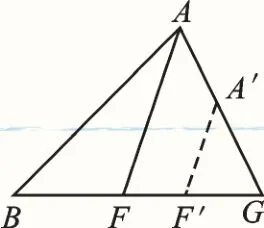
图4
二、对原题的变式
【变式一】由特殊到一般.
如图5,若∠B=∠C=∠FAG,例题中的结论还成立吗?为什么?
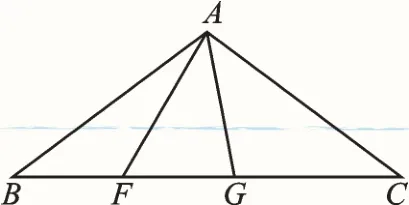
图5
【解析】由“两角法”,仍然可判定△BGA∽△AGF∽△CAF.
【点评】注意“特殊”和“一般”的关系,一般条件下成立的结论,在特殊条件下仍然成立,反之则不一定.
【变式二】增加旋转变化.
如图6,把原题中的△DEA绕点A旋转,使AD、AE分别交边BC及其延长线于点F、G(点F、G与点B、C不重合),例题中的结论还成立吗?为什么?
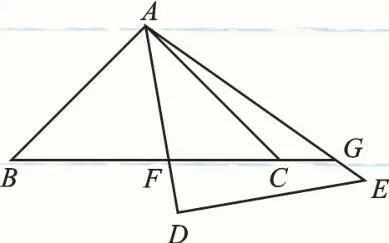
图6
【解析】本题在旋转后,对应角相等的关系没有变,所以例题的结论仍然成立.
【点评】本题和原题一样,仍然可以把图形分解成“共角共边型”相似模型,所以结论仍然成立.其实,如果把△DEA绕点A顺时针或逆时针旋转,边AD、AE或其延长线与边BC所在的直线只要相交于点F、G(不与点B、C重合),则例题的结论始终成立.
【变式三】改变图形的位置.
如图7,△ABC和△DEF是两个全等的等腰直角三角形,∠A=∠D=90°,点E是斜边BC上一动点,△DEF的两边分别和△ABC的两直角边交于G、H两点.
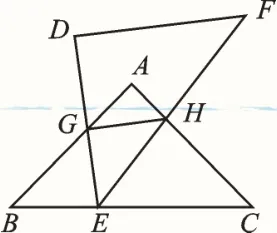
图7
(1)试判断△BGE和△CEH是否相似?为什么?
(2)连接GH,当点E运动到BC边什么位置时,△EGH和△BGE相似?并说明理由.
【解析】(1)由“两角法”易证△BGE∽△CEH.
(2)当点E运动到BC边的中点时,△EGH∽△BGE.由△BGE∽△CEH可得又CE=BE,所以又∠B=∠GEH=45°,所以△EGH∽△BGE.
【点评】本题通过改变等腰直角三角形的位置,构造新图形,提出新问题.第(1)题仍然用“两角法”判定两个三角形相似,和例题一样,其实只要有∠B=∠GEH=∠C,结论就成立.第(2)题当点E运动到特殊位置(BC边中点)时成立,由第(1)题的相似得对应边成比例,再进行“等线段代换”,从而用“两边成比例且夹角相等的两个三角形相似”判定出结论.
三、对原题及变式的反思
“等腰直角三角形”是一种特殊的三角形,有其“特殊性”,如:三个内角之比是1∶1∶2,三边之比是1∶1∶ 2,斜边上的高把原三角形分成两个全等的等腰直角三角形等,在解题时要学会充分运用这些特殊的性质.
用两个等腰直角三角形可以构造出很多图形,原题把一个三角形的直角顶点和另一个三角形的锐角顶点重合,从而构造出“共角共边型”相似三角形.变式一抓住“三个角相等”的本质,从“特殊”推广到“一般”,使其“一般化”.变式二仍然抓住“三个角相等”的本质,增加旋转变化,从“边边相交”推广到“边边所在直线相交”,将其“一般化”处理.变式三改变两个三角形的组合方式,尽管图形的位置发生了变化,但角的大小没有变,仍然可以由“基本条件——两角相等”得到“基本结论——相似”.变式的目的是在图形发生变化的情况下寻求不变的方法.同学们在遇到此类问题时,只要善于抓住“基本模型”,灵活运用“基本方法”,问题就能迎刃而解.



