文南京师范大学第二附属初级中学八(6 6)班 李晨玥 刘昕
“道生一,一生二,二生三,三生万物。”任何事物的发展都遵循着由简到繁、由浅入深的规律,数学中的“全等”也不例外,通过严密审题后的步步推论,由已知到未知,从未知中获取相关结论。下面,结合两道题目谈谈解决复杂全等问题的思路和方法,与大家分享。
例1如图1,已知:BE=CD,∠BDO=∠CEB。求证:△BDO≌△CEO。
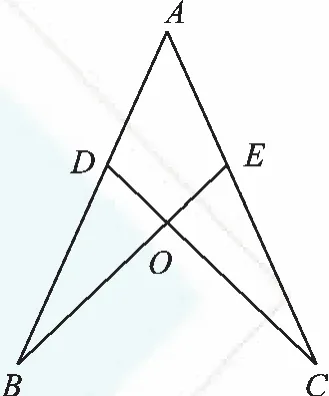
图1
【分析】在△BDO与△CEO中,目前只有∠BDO=∠CEB、∠BOD=∠COE,很显然,缺少一组相等的边,无法直接证明全等。据此,我们认为本题中应存在比较容易证明的全等。在△BDO与△CEO中,∵∠BDO=∠CEB,∠BOD=∠COE,∴∠B=∠C;又∵∠A=∠A,BE=CD,显而易见,可以用“AAS”证明△ABE≌△ACD,从而得到 AD=AE、AB=AC,则 DB=EC。接下来只需利用“AAS”证明△BDO≌△CEO即可。
【感悟】解答此类较为复杂的全等问题,当题中所给的条件不能直接证明时,我们要仔细分析边与边、角与角之间的等量关系,寻找容易证明的全等,这样,复杂的问题就迎刃而解了。其实我们经历了下面一个思维过程:

例2如图2,∠E=∠F=90°,AE=AF,∠B=∠C。现给出下列判断:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=BD。其中正确的有___________ 。
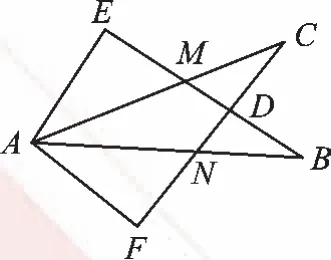
图2
【分析】通览四个结论,③中的两个三角形看起来形状相同、大小相等,我们可以先大胆猜想它们是全等的,但根据已知条件不能直接解决,那我们应该从最简易的全等入手。
根据已知条件,我们不难得出△AEB≌△AFC(AAS),可得∠EAB=∠FAC ,所以∠FAN=∠EAM,故①正确。
对于②,只需考虑EM和FN所在的三角形是否全等,即证明△AEM是否全等于△AFN。由结论①不难得到△AEM≌△AFN,从而可知EM=FN,故②正确。
对于③,现已知∠CAN=∠BAM,∠C=∠B,缺少“边”相等,而由②△AEM≌△AFN,易得AN=AM,从而可得△ACN≌△ABM(AAS),故③正确;
对于④,和②的思路一样,只需考虑CD、BD所在三角形是否全等,即证明△CDM是否全等于△BDN。由②△AEM≌△AFN可得AM=AN;又因为AC=AB,所以 CM=BN,则可证得△CDM≌△BDN,所以CD=BD。故④正确。
所以①②③④均正确。
【感悟】我们发现,四个结论由浅入深,层层递进。从题目所给的条件,由最简单的全等三角形入手,用它的结论继而挖掘出更多的较为复杂的全等三角形是解决本题的策略。整个解题思路,让我们体会到“数学链”的味道,环环相扣,也体现出数学思维的连贯性、逻辑性和严密性。所以做此类多项选择的题目时,应立足根本,循序渐进。值得注意的是,有时也需要适当变换证明所给结论的顺序。
教师点评
解决数学问题有着和大侦探破案一样的“味道”,一样能获得成就感。这篇文章中,小作者发现了研究较为复杂的全等三角形的思路:
小作者进而感悟到数学思维的连贯性、逻辑性和严密性。
其实,我们研究其他类型的数学难题时,若也能由浅入深,循序渐进,将会有“水到渠成”“拨云见日”的效果。



