文方智娟
(作者单位:安徽省合肥市北城力高学校)
圆的对称性给人以美的感受,而与圆相关的知识点却比较多,对初学者来说易产生困惑。有关圆的求解问题一般可转化为求角、边(或线段)以及最值问题,下面以几组经典题目帮助同学们有效学习与掌握。
一、求角
例1 如图1,菱形ABOC的边AB、AC分别与⊙O相切于点D、E,若点D是AB中点,则∠DOE= 。
【分析】由切线性质可知OD⊥AB,OE⊥AC,又结合中点得OD为AB的中垂线,再根据题意,可得OA=OB=AB=AC=OC,得到两个等边三角形。
解:连接OA,如图2,
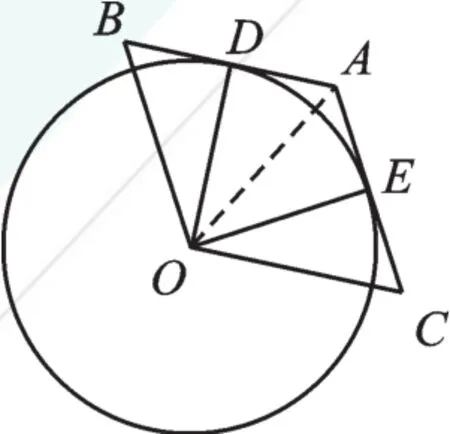
图2
∵AB、AC分别与⊙O相切于点D、E,
∴OD⊥AB,OE⊥AC。
又点D为AB的中点,
∴OA=OB=AB=AC=OC,
∴△AOB与△AOC都是等边三角形,
∴∠BAO=∠CAO=60°,
∴∠BAC=∠BAO+∠CAO=120°,
∴∠DOE=180°-∠BAC=60°。
故答案为60°。
【点评】本题巧妙地将特殊的平行四边形与圆相结合,考查基本图形、基本概念及相关性质。理解切线的性质,厘清垂直平分线、等腰三角形“三线合一”以及等边三角形的知识点是解决问题的基础和关键。
例2 如图3,⊙A过点O(0,0),C( 3,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO、BD,则∠OBD=( )。
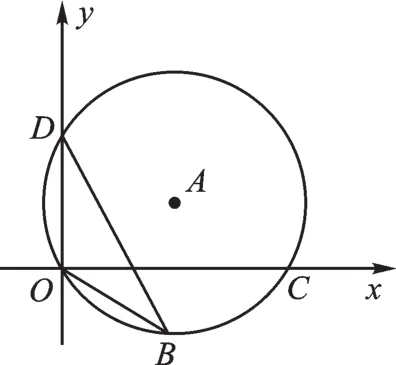
图3
A.15° B.30° C.45° D.60°
【分析】如果连接CD,根据在同一圆中,同弧所对的圆周角相等,得∠OBD=∠OCD,由DO⊥OC,结合平面直角坐标系和解直角三角形知识得到解决。
解:连接CD,如图4,易得∠OBD=∠OCD。
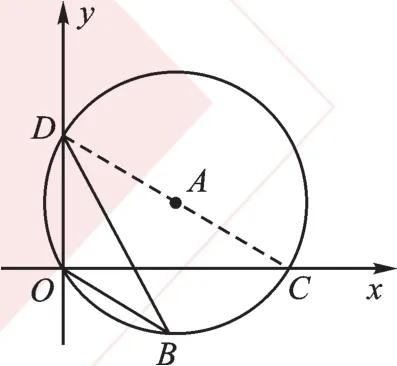
图4
∵DO⊥OC,OC=3,OD=1,
∴在Rt△COD中,
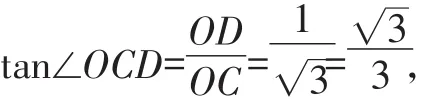
∴∠OCD=30°,∴∠OBD=30°。
故选:B。
【点评】解题的核心与关键是“转化思想”的运用,一是将∠OBD转化为与它相等的角(图中的∠OCD),二是将∠OBD所在的非直角三角形转化为直角三角形(构造直角三角形)。通过连接CD,有效利用同一圆中同弧所对的圆周角相等、直角所对的弦是直径以及锐角三角函数进行解题。
二、求边或线段
例3 如图5,AB是⊙O的直径,AB⊥CD于点E,AB=10,CD=8,则BE的长为( )。
A.2 B.3 C.4 D.3.5
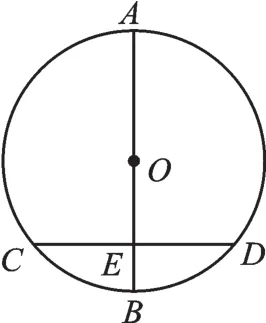
图5
【分析】连接OC,如图6,根据勾股定理,求出OE。
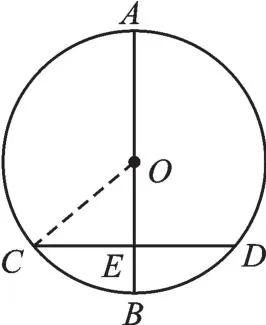
图6
解:连接OC,
∵AB=10,AB为⊙O的直径,
∴OB=OC=5,
∵AB⊥CD,CD=8,
在Rt△OCE中,

∴BE=OB-OE=2。
故选:A。
【点评】本题是根据垂径定理构造直角三角形。垂径定理、勾股定理等是解决很多问题的有效途径和方法。
例4 如图7,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于点D,E为⁀CD的中点,连接CE、BE,BE交AC于点F。若AB=3,BC=4,求CE的长。
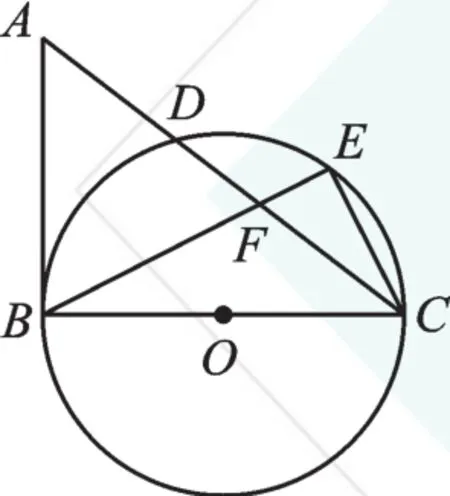
图7
【分析】可以通过证明∠ABE=∠AFB得AB=AF,接下来通过△BEC∽△CEF,得到BE=2CE,然后再利用勾股定理即可。
解:∵∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵BC为⊙O直径,∴∠BEC=90°,
∴∠EFC+∠ECF=90°。
又∠EFC=∠AFB,
∴∠AF⁀B+∠ECF=90°。
∵E为CD的中点,
∴∠CBE=∠ECF,
∴∠ABE=∠AFB,∴AB=AF。
在Rt△ABC中,AB=3,BC=4,
∴AC=5,由AF=AB=3,
∴CF=AC-AF=2,
∵∠CBE=∠ECF,∠BEC=∠CEF=90°,
∴△BEC∽△CEF,
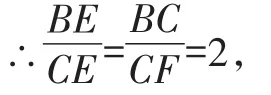
∴BE=2CE,
又BE2+CE2=BC2,

【点评】本题方法不唯一,还可以通过连接BD来解决,同学们可自己尝试。
三、求最值
例5 如图8,在△ABC中,∠ABC=90°,∠A=30°,BC=2,点Q是AC的中点,则点Q到以AB为直径的圆上任意一点的距离中,最大值为_____ ,最小值为_____。
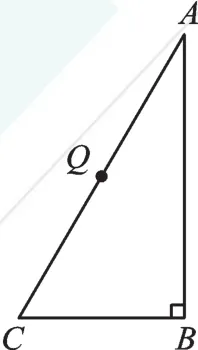
图8
【分析】题目条件将本来已经存在的图“隐”起来了。如果有了图9,不仅看起来直观了,而且解决问题的思路也明了了。
解:如图9,以AB为直径作⊙O,过点O、Q作直径与⊙O交于点P1,P2,
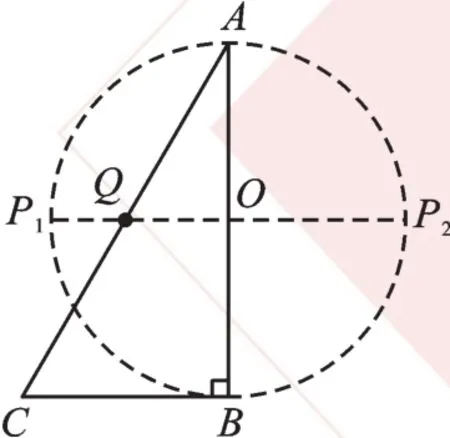
图9
在Rt△ABC中,∠A=30°,BC=2,

【点评】让“隐圆”显现出来,问题迎刃而解。分析问题,添加辅助线,应朝着有助于解决问题的方向努力。



