文李爱民
所谓“转化”,就是将一个问题的解决转向另一个问题的解决,以达到化生疏为熟悉,化复杂为简单,化抽象为直观的目的的数学方法。初中阶段,我们就借助转化的思想方法学习了不同类型方程的解法。首先,我们利用等式的性质归纳出一元一次方程的解法;接着,通过消元将解二元一次方程组转化为解一元一次方程,通过降次将解一元二次方程转化为解一元一次方程,通过去分母将解分式方程转化为解整式方程。下面,老师再举一些例子,让同学们感受“转化”在方程和不等式中的应用。
一、通过“换元”实现转化
例1若(a2+b2)2-2(a2+b2)-3=0,则代数式a2+b2的值为( )。
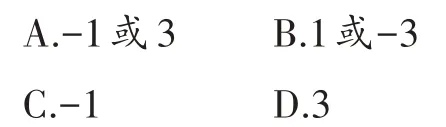
【分析】将a2+b2看成整体,通过换元可以将原方程转化为一元二次方程求解。
解:设a2+b2=x,则原方程变形为x2-2x-3=0,解得x1=3,x2=-1。因为a2+b2≥0,即x≥0,所以x=3,所以a2+b2=3,所以答案为D。
【点评】本题考查用换元法解一元二次方程,解题的关键是能想到将a2+b2整体设元,同时还要注意a2+b2的取值范围。
二、通过“数形结合”实现转化
1.以形助数。

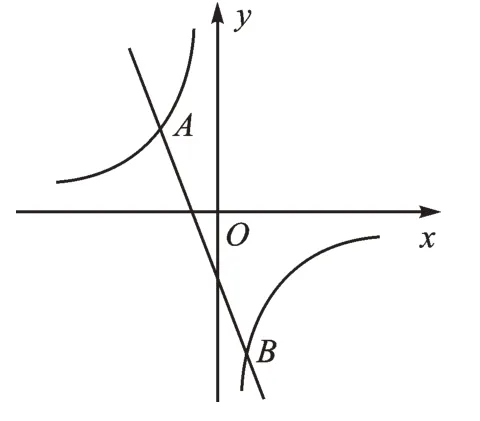
图1
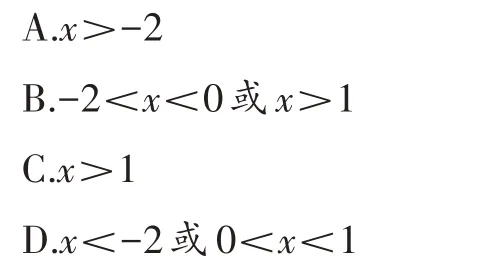
【分析】已知点A、B,可以用待定系数法求出两个函数的表达式,这样就可以得到一个明确的不等式,但求解过程比较复杂。仔细观察,不难发现:解不等式实际上是比较两个函数的大小,借助图像可以简单直观地得到答案。
解:因为两个函数相交于点A、B,所以当x=-2 和x=1 时,两个函数值相等。因为反比例函数的自变量x≠0,所以比较两个函数的大小关系可以将自变量x分成4 个部分,分别是:x<-2、-2<x<0、0<x<1、x>1。观察函数图像,不难发现当x<-2 或0<x<1 时,一次函数图像在反比例函数图像上方,即kx+b>所以本题的答案为D。
【点评】本题以数的形式出示问题,表面是解不等式,但发现直接求解比较困难。因此,我们可以借助函数的背景,从形的角度入手,将其转化成比较两个函数大小的问题。函数与方程、不等式有着密切的关系,当出现以函数为背景的方程、不等式问题时,往往可以借助函数图像解决。
2.以数解形。
例3若关于x的一元二次方程x2-2x+kb+1=0 有两个不相等的实数根,则一次函数y=kx+b 的大致图像可能是( )。
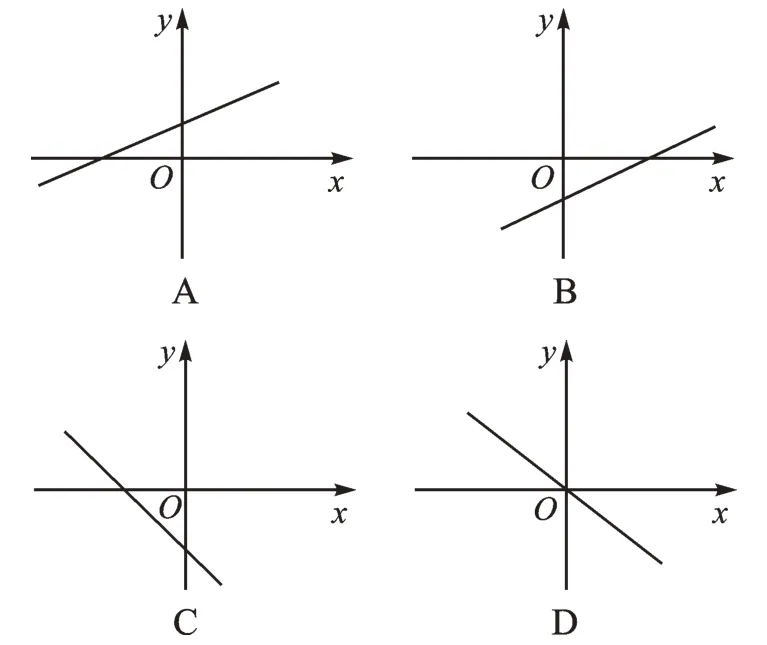
【分析】由根的判别式可以求出kb的范围,再结合一次函数图像与k、b 的关系可以确定出大致的图像。
解:因为一元二次方程x2-2x+kb+1=0 有两个不相等的实数根,所以根的判别式Δ>0,所以4-4(kb+1)>0,解不等式得kb<0,所以k 与b 异号,即k>0,b<0或k<0,b>0。当k>0,b<0时,一次函数的图像经过一、三、四象限;当k<0,b>0 时,一次函数的图像经过一、二、四象限,所以选B。
【点评】本题求一次函数的图像,是形的问题,但一次函数的图像由k、b 决定,必须依靠数的计算,所以转化为解不等式的问题。
三、通过“分类讨论”实现转化
例4若关于x的方程(a-1)x2+3x-2=0有实数根,求a的取值范围。
【分析】因为二次项系数(a-1)不确定,所以方程的类型不确定。先对(a-1)进行讨论,确定是何种方程,再分别求解。

【点评】本题主要考查分类讨论思想。通过对二次项系数的讨论,我们将原方程转化为一元一次方程和一元二次方程,达到化含糊为清晰的效果,能有效考查思维的严密性。
四、通过“构造”实现转化
例5若实数a≠b,且a、b分别满足a2-8a+5=0,b2-8b+5=0,求 代 数 式a2b+ab2的值。
【分析】我们观察两个等式中系数的特点,发现可以构造出一元二次方程,再借助根与系数的关系求出代数式的值。
解:因为a、b分别满足a2-8a+5=0,b2-8b+5=0,并且a≠b,所以a、b可以看成方程x2-8x+5=0 的两个不相等的实数根,所以a+b=8,ab=5,所以a2b+ab2=ab(a+b)=5×8=40。
【点评】我们如果“暴力”解出a、b的值,再求解代数式的值,会发现解题过程比较复杂,而且计算量大,容易出错。通过逆用根的意义构造一元二次方程,能巧妙地将问题转化,达到化繁为简的效果。
方程和不等式是“数与代数”的核心内容,是刻画现实世界数量关系的有效模型,是解决其他数学问题的重要工具。所以同学们要掌握方程和不等式的基本概念、性质、解法、应用,更要能感悟其中隐藏的“转化”的思想方法,并善于将这种方法迁移到其他知识的学习中,这将对我们的学习有很大帮助。



