全等三角形的“一”与“多”

文／李静

中考复习中，经常会出现一题多解、一题多变、多题归一的情况。下面以全等三角形为例，提炼数学思想方法，希望能帮助同学们真正做到融会贯通。

类型一：一题多解

如图1，P是∠CAB的平分线上的一点，分别在射线AB、AC上确定点D、E，使△APD≌△APE，你有什么办法？并说明你的依据。

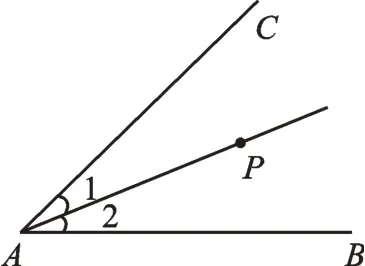
图1

【分析】∠1=∠2，AP=AP是已知的，要确定点D、E，使△APD≌△APE。判定三角形全等的方法有ASA、SAS、AAS，还有SSS。从已知看，我们已经有了一个角和一个边，那么前三个判定定理会更适合。

方法1：以点A为圆心，适当的长为半径作圆弧，与AB、AC分别交于点D、E，利用“SAS”来证明△APD≌△APE。

方法2：过点P作DE⊥AP，DE交AB于点D，交AC于点E，利用“ASA”来证明△APD≌△APE。

方法3：过点P分别作PD⊥AB于点D，PE⊥AC于点E，利用“AAS”来证明△APD≌△APE。

方法4：过点P作PD∥AC交AB于点D，PE∥AB交AC于点E，利用“ASA”来证明△APD≌△APE。

【总结】在寻找点的过程中，一定要利用好已知的条件，明确解题目标，有的放矢地去寻找点D和点E。

以类型一中的方法3 画对应的图形为例，连接DE，请猜想关于线段DE和线段AP之间存在什么样的位置关系？

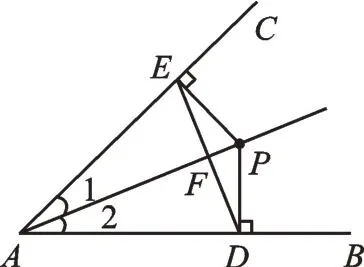
图2

【分析】猜想“AP垂直平分线段ED”。证明方法不唯一，可以先通过三角形全等证明AE=AD，PE=PD，再用垂直平分线的定义来证明，也可以先通过证明△AEF≌△ADF或△PEF≌△PDF，再用垂直平分线的定义来证明。

【总结】由此我们可得到这样一个结论：已知P是∠CAB的平分线上一点，若PD⊥AB于点D，PE⊥AC于点E，连接ED交AP于点F，则AP垂直平分ED。如果这道题的条件做一些变化，该怎么处理？

变式已知：如图3，P是∠CAB的平分线上一点，∠3+∠4=180°。求证：PD=PE。

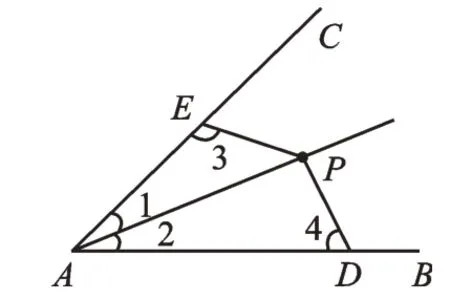
图3

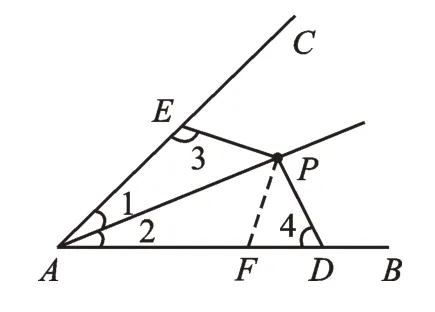
图4

方法1：在AB上取一点F，使AE=AF，如图4，再通过∠1=∠2，AP=AP，根据“SAS”，得△AEP≌△AFP，从而∠3=∠AFP，EP=FP。又因为∠3+∠4=180°，∠AFP+∠PFD=180°，故∠PFD=∠4，从而PF=PD，所以PE=PD。

方法2：在AC上取一点F，使得AF=AD，如图5，再通过∠1=∠2，AP=AP，根据“SAS”，得△ADP≌△AFP，从而∠4=∠PFA，FP=DP。因为∠3+∠4=180°，∠3+∠PEF=180°，故∠PEF=∠4，从而∠PEF=∠PFE，进一步得到EP=FP，所以PE=PD。

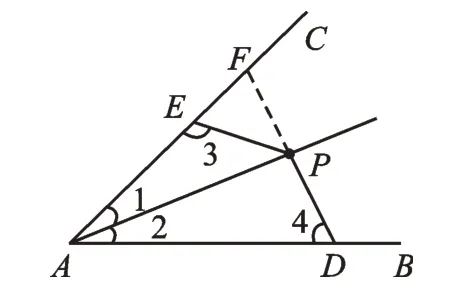
图5

方法3：通过证明两个三角形全等这一途径来达到证明两条线段相等的目的。在AB上取一点F，使AP=FP，如图6，则∠PFA=∠2=∠1。因为∠3+∠4=180°，∠4+∠PDF=180°，所以∠3=∠PDF，根据“AAS”，可得△AEP≌△FDP，从而PD=PE。

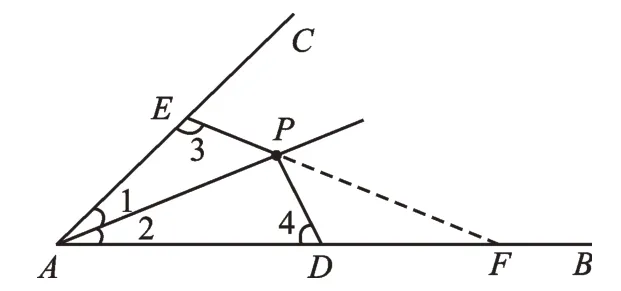
图6

【总结】变式的解法不止这3 种。因此，在一题多解的基础上，通过题目的变化，我们可以对三角形全等的判定进行更加深入的思考。

已知：如图7 所示，在△ABC中，∠CAB和∠CBA的平分线AD、BE相交于点P，且AE=BE，∠3=40°。求证：PE=PD。

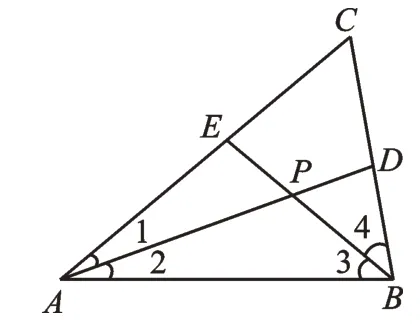
图7

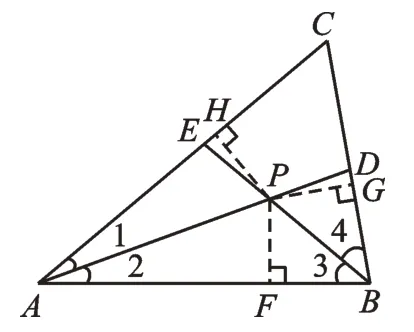
图8

方法1：根据角平分线，联想到作PF、PG、PH分别垂直AB、BC、AC，垂足分别为F、G、H。因为AD、BE分别平分∠CAB、∠CBA，可以得到PH=PF=PG，且∠PHE=∠PGD=90°。我们很容易得到∠PDB=∠PEH=80°，根据“AAS”，可证明△PEH≌△PDG，从而PE=PD。

方法2：在AB上取一点F，使AE=AF。由∠1=∠2，AP=AP，根据“SAS”，得到△AEP≌△AFP，从而∠EPA=∠FPA=60°，EP=FP，从而∠FPB=∠DPB=60°，结合∠3=∠4，PB=PB，根据“ASA”，可以证明△FPB≌△DPB，故DP=FP=EP。

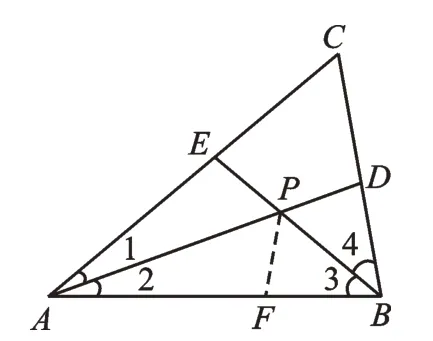
图9

【总结】我们从刚才几个题目不难发现，可以找第三个量作为关联量，来证明另外两个量相等。这就是数学知识的关联性。