梅 芳 曾春华 王巧玲
(江西农业大学 理学院,江西 南昌330045)
对于分析、解答处理问题的思维方法,逆向思维方法与顺向思维方法相对而言的。顺向思维是按照已知条件出现的先后顺序进行思考的;而逆向思维是是从反方向(或从问题的结果)出发,不依照问题出现的先后顺序,从而逆转推理的一种思维方法。
1 概率论与数理统计和反例教学法
在概率论与数理统计的教学中会碰到许多用逆向思维求解的内容,例如,显着性假设检验的原理是小概率事件实际不可能原理,在一次实验中小概率事件是不会发生的,但是在一次显着性假设检验过程中小概率事件居然发生了,说明原命题是假的。统计中大量的反例教学是教学中的难点,也是学生理解概率统计问题的难点。我们知道,要断定一个命题正确,必须经过严密的推理论证,而要否定一个命题,只要能举出一个与结论矛盾的例子就可以了,这种与命题相矛盾的例子称为反例。反例教学法是从原问题的相反方向着手的一种思维教学法,对于某些特定的问题,从结论倒过来思考,会使得问题清晰简单。它是数学思维的一个重要方面,是创造性思维的一个组成部分,也是进行思维训练的载体。在概率论与数理统计教学中始终贯穿反例教学法,是培养学生逆向思维的过程也是培养学生思维敏捷性的过程。
本文以大学数学公共课概率论与数理统计课程教学中的事件与概率一章为例,归纳总结反例教学法在此章节的应用与研究。
2 三个典型性结论及其反例
在教学过程中,随机事件及其概率这一章节中的可以归纳出很多个理论公式和结论,本文中只是举三个典型性结论,然后举出反例加以推理验证,刺激学生的好奇心和兴趣,从而使得学生更加透彻的理解数理统计概念,更加好学,更加具有专研精神,更有助于学生数学思维的培养。
符号:
A,B,C:随机事件
Ω:必然事件;样本空b间;
Ø:不可能事件
定理1 用事件的运算关系表示事件的方法不一定唯一
例如,用A,B,C的运算关系表示事件D={A,B,C中不多于一个事件发生},根据事件的和、差、积及其逆事件的概念,可以写出下面四种不同的表示法:
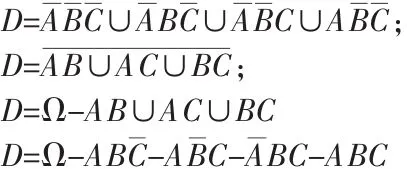
定理2 样本点不一定是事件
按照概率的公理化体系可知,样本点是样本空间Ω的元素,而事件是事件域中F中的元素,它是样本点的某些子集.在古典概型中,样本空间Ω只含有穷个点,所以Ω也是有穷的.此时常常把Ω的一切子集都视为事件.但却不能由此认为样本点一定是事件.实际上,并不把Ω的一切子集都当作事件来研究。
例如,现从标有数字1~10的十个球,任取一球,样本空间
Ω={1,2,…,10}
令
A={所取球的号码为偶数}={2,4,6,8,10}
A={所取球的号码为偶数}={1,3,5,7,9}
我们只考虑事件Ø,A,A,Ω时,容易验证F={Ø,A,A,Ω}为一事件域,于是Ω中的样本点B={所取球的号码为4}就不是事件域F中的元素,即B={4}不是F中的事件。
定理3 对“等可能性”的理解不同,得到的概率不一定相同
在概率论发展的早期,大部分的人都相信,只要找到适当的等可能性描述,就可以给概率问题唯一的解答,但事实上确并非如此,这是个经典的着名反例,贝特朗(Bertrand)奇论(贝特朗在1887年出版的《概率论教程》一书中构造了这个例子):
在半径为1的园内随意画一条弦,问它的长度超过其内接正三角形的边长的概率等于多少?
从不同的方向的理解,贝特朗对这个问题给出了三种不同的解法。

图1
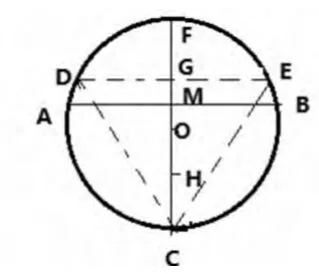
图2

图3
解法一:
如图1,我们在圆中任意画一条弦AB,又以A为定点作圆的内接正ΔACD,要AB比AC(容易计算出)长,由已知,必须端点B落在弧CD上,点B落在圆周上任何一点是等可能的,于是,AB超过的概率为

解法二:如图2,在圆中任意画出一条弦AB,再作与AB垂直的直径CF,并以C为顶点作圆的内接正ΔCDE,由图可见,要AB>DF,必须AB和直径CF的交点M落在GH内,这里G是CF与DE的交点,H是G关于圆心O的对称点,由平面几何可以求出M点落在CF上各点是等可能的,故AB超过的概率为:

解法三:如图3,在圆中任意画出一条弦AB,再作圆内接正ΔCDE,使得DE//AB。接着作出ΔCDE的内切圆,计算出内切圆的半径设AB的中点为Q,很明显Q点必须落在这个内切圆(阴影部分)内,AB的长才不会超过落在大圆内任何一点都是等可能的,故所求的概率为:

三种解法推理看起来都无懈可击,不同的理解得到了三种完全不同的答案,从而使得问题得到了奇论的美称,也就是数学上的贝特朗悖论。同一个问题得到不同的结论的原因是什幺呢?原因在于每种解法对于“等可能性”作出了不同的理解和假设:解法一假定了弦的端点落在圆周上各点是等可能的;解法二假定了弦的中点落在直径上各点是等可能的;解法三假定了弦的中点落在圆内各点上是等可能的。对于各自不同的假设,上面三种解法和结果都是正确的,这个例子提醒学生,在解答概率问题时,一定要弄清楚等可能性的条件,以免发生混淆。
3 结束语
在概率论与数理统计的教学过程中的引人各种反例教学,会使得上课更加生动有趣,不同于常规的思维推理一定会引起学生的好奇心和好胜心,从而激发学生对概率统计的极大兴趣,然后可以引导学生专研问题,思考结论。在教学中插入恰当的反例,即是简明有力的否定方法,又是加深学生对概念和定理的理解的重要手段,它有助于发现问题,活跃思维、避免常犯易犯的错误。从而达到教学上的最高水平,取得令人满意的教学效果。
[1]盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.高等教育出版社,2008:1-14.
[2]沈恒范.概率论与数理统计[M].5版.高等教育出版社,2011:1-7.
[3]袁荫棠.概率论与数理统计[M].2版.人民大学出版社,1990:1-14.



