魏宁,占萌颖,郑立飞,万阿英
(1.西北农林科技大学理学院,陕西杨凌712100;2.西北工业大学计算机学院,陕西西安710000;3.呼伦贝尔学院数学与统计学院,内蒙古海拉尔021008)
1.引言
种群的持续生存是数学生态学中捕食理论的一个重要而广泛的问题.对于捕食者-食饵系统,很多学者已有大量的研究工作[1-10].同时,越来越多的生物学和生理学证据表明,在许多情况下,特别是当捕食者不得不搜寻食物,因此不得不分享或竞争食物时,一个更切合实际并且更一般的捕食者-食饵系统模型应该是:捕食者的捕食率除了和食饵种群的种群密度有关外,还受到捕食者种群自身的密度影响.因此一般的捕食者-食饵系统模型可描述为

其中ai,bi,ci(i=1,2)均为正常数.采用Holling第二型功能反应项,该模型可以改进为

其中ai,bi(i=1,2),α,k,m均为正常数.
然而,人们发现在现实问题当中,一个系统将来的状态不仅仅只是和当前的状态有关同时它也与过去的某一时间段有紧密的联系.所以,近年来具有时滞的捕食者-食饵系统模型倍受广泛关注.在模型(1)和(2)的基础上,本文主要考虑如下时滞系统

其中,N1(t),N2(t)分别是食饵和捕食者的种群密度,bi:R→R,ai,τi,σi,α:R→[0,+∞),β:R→[0,+∞)是连续的ω周期函数且α/0.m≥0,当m=0时系统(3)是经典的Lotka-Volterra捕食者-食饵模型.
本文的目的是利用Mawhin重合度理论中的延拓定理来研究系统(3)正ω周期解的全局存在性.
2.预备知识
本文利用Gaines和Mawhin重合度理论中的延拓定理证明系统(3)周期解的存在性.
设X,Z是两个Banach空间,L:DomL⊂X→Z为线性映射,N:X→Z为连续映射.如果dim KerL=co dim ImL<+∞且ImL为Z中的闭子集,则称映射L是指标为0的Fredholm映射.若L指标为0的Fredholm映射存在连续投影

使得

则L|DomL∩KerP:(I-P)X→ImL可逆,并设其逆影射为KP.
设Ω为X中的有界开集,若QN()有界且KP(I-Q)N:→X是紧的,则称N在上是L-紧的.由于ImQ和KerL是同构的,因而存在同构影射J:ImQ→KerL.
引理1[11](延拓定理)设X,Z是Banach空间,L指标为0的Fredholm映射,N:X→Z在上是L-紧的,其中Ω为X中的有界开集,且满足:
1)∀λ∈(0,1),方程Lx=λNx的解满足;
2)∀x∈Ker0;
3)deg{JQN,Ω∩KerL,00.
则方程Lx=Nx在DomL∩内至少存在一个解.
引理2关于系统(3)是正向不变的.
证因为

显然引理的结论成立.
结合系统(3)的实际生物学意义,取如下初值

且假设种群密度有界,即
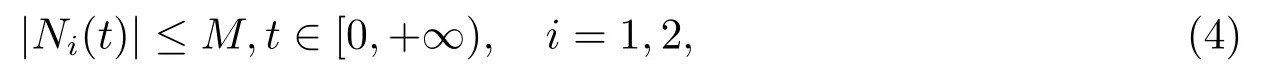
其中,τ=max{τ1(t),τ2(t),σ1(t),σ2(t)}.本文采用如下的记号:
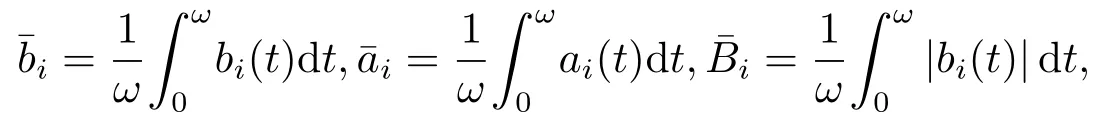

3.主要结果及证明
本文主要结果为如下的定理.
定理1如果则系统(3)至少存在一个正ω周期解.
证首先作变换

则系统(3)可变形为


则X,Z在范数‖·‖下为Banach空间,令

则

为Z中的闭子集,且dim KerL=2=co dim ImL.因此,L是指标为0的Fredholm映射.容易证明,P,Q是连续的投影算子且使得ImP=KerL,ImL=KerQ=Im(I-Q),故L的逆映射Kp:ImL→KerP∩DomL存在,且

从而


显然,由以上两式可知QN及Kp(I-Q)N也连续,因为Ω为X中的有界开集,则QN()有界,利用Ascoli-Arzela定理,容易证明是紧致的,因此N在上是L-紧的.
对应于算子方程Lx=λNx,λ∈(0,1),有

设x(t)∈X是系统(6)对应于某个λ∈(0,1)的解,对系统(5)两端由0到ω积分得
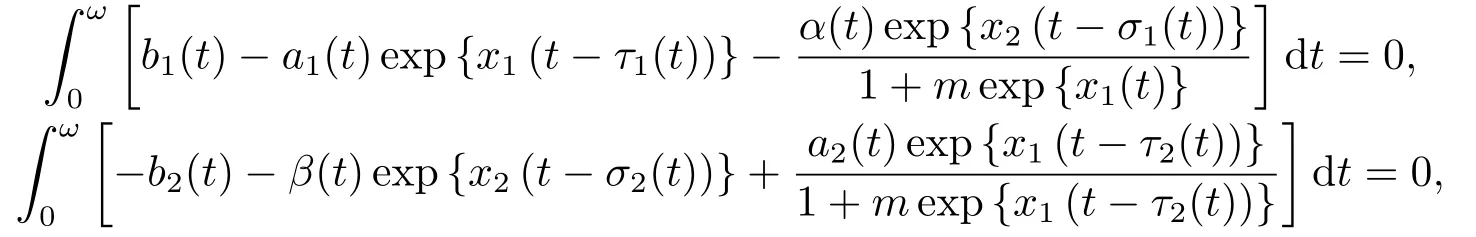
即

由(6)-(8)知
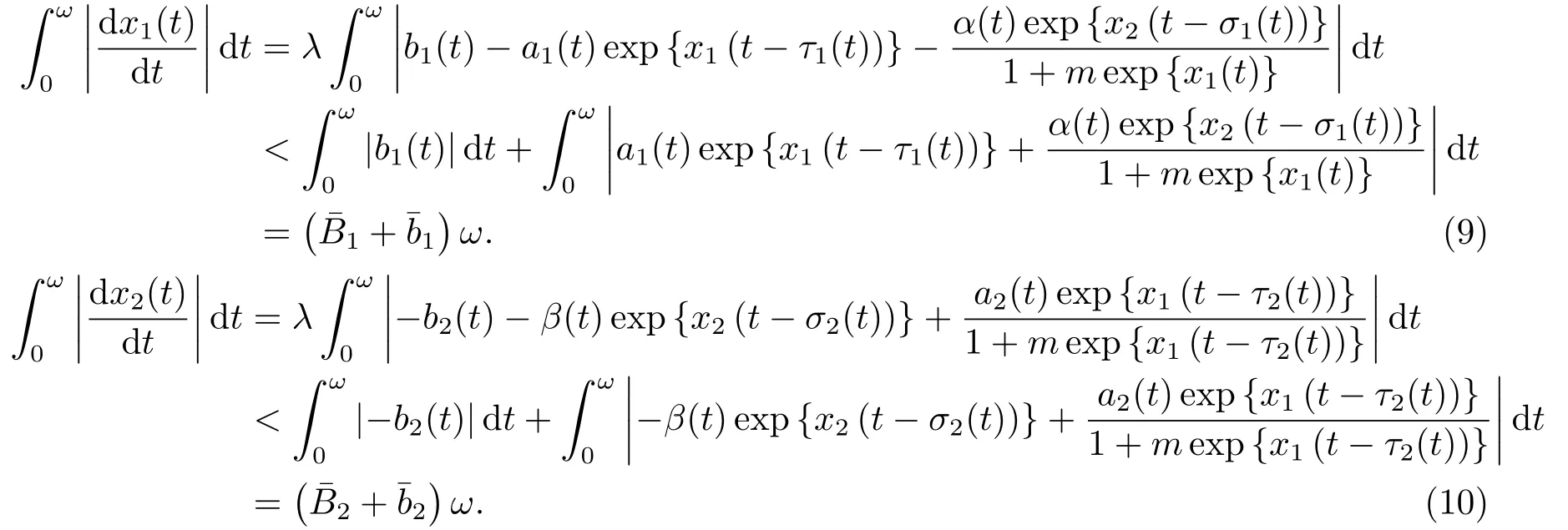
因为x(t)=(x1(t),x2(t))T∈X,所以存在ξi,ηi∈[0,ω],i=1,2,使得

由(4),(7)及(11),有
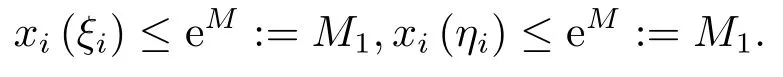
且

即

于是

另外,由(7)及(10)还可以得到
即

于是

由(12),(13),有

由(7)式有

所以

则

由(7),(10)及(12)可得


所以
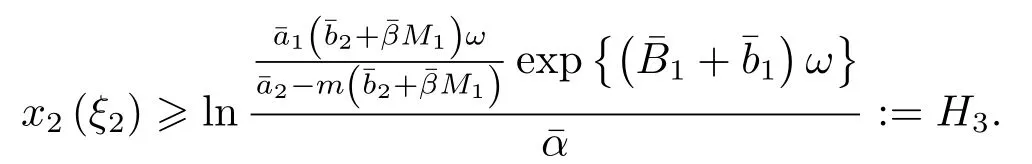
则

由(15),(16)可知

由式(13)-(16),可以看出Hi(i=1,2,3,4)与λ的选取无关,由定理的已知条件容易证明代数方程组


令

则Ω满足引理1中的条件,当x∈∂Ω∩KerL=∂Ω∩R2时,x是R2中的常值向量且‖x‖=H,于是
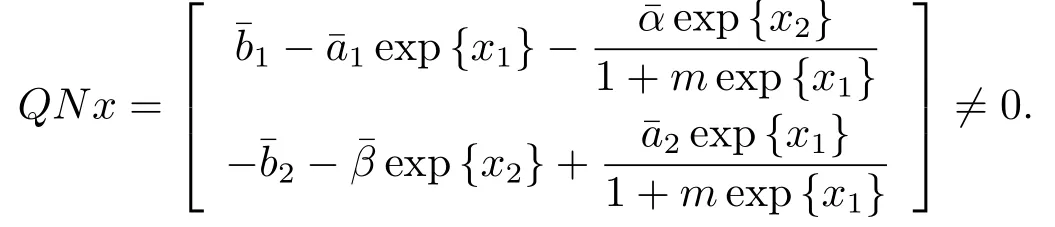
又式(16)存在唯一解,由已知条件可直接计算得到

此式中同构映射J可取为恒同构映射,因为KerL=ImQ.由于已经证明Ω满足引理1的全部条件,由引理1,方程Lx=Nx在DomL∩中至少存在一个解,即系统(3)在中至少存在一个ω周期解令则由(4)可知是系统(3)的一个ω周期解.
注1系统(3)中τ1(t),τ2(t),σ1(t),σ2(t)不必恒为正数.
注2此结论对食物链系统模型仍然成立.
注3当m=0时,系统(3)的周期解仍然存在.



