文/许燕

圆是一种“完美”的图形,其完美性不仅体现在它既是轴对称图形,又是中心对称图形,还体现在它的旋转不变性。由圆的对称性引出了许多重要的定理,为本章的计算与证明提供了依据。下面,我们将通过一组典型例题,和大家共同探讨圆中有关问题的解题策略。
一、理解记忆,掌握基本结论
例1如图1,在Rt△ACB中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕A点顺时针旋转90°得到Rt△AED,则BC扫过的面积为_____。
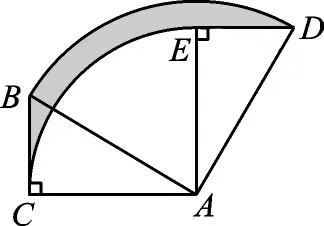
图1
【解析】∵在Rt△ACB中,∠BCA=90°,∠BAC=30°,BC=2,∴AB=4,AC=。
∴BC扫过的面积:
【策略方法】我们要理解弧长、扇形面积、圆柱面积、圆锥面积的推导过程,并学会从实际问题中抽象出数学问题,通过转化思想,将复杂图形进行分解转化。
二、巧妙“添线”,熟悉基本性质
例2把球放在长方体纸盒内,球的一部分露出盒外,其截面如图2,已知EF=CD=8cm,则球的半径长是( )。

图2
A.4cm B.5cm C.6cm D.8cm
【解析】设圆心为O,过点O作ON⊥AD于点N,延长NO,交CB于点M,连接OF,如图3。

图3
∵四边形ABCD是矩形,
∴∠C=∠D=90°。
∴四边形CDNM是矩形。
∴MN=CD=8。
设OF=x,则OM=OF,
∴ON=MN-OM=8-x,NF=EN=4。
在Rt△ONF中,ON2+NF2=OF2,即(8-x)2+42=x2,解得x=5。故选B。
【策略方法】由圆的对称性能引出许多重要的定理和推论,这些性质在计算和证明等方面有广泛的应用。一般来说,我们可以通过添加辅助线构造直角三角形,利用勾股定理来解决问题。
三、动中求静,探寻本质规律
例3如图4,在△ABC中,∠ACB=90°,AC=5cm,AB=13cm,将△ABC绕点C按顺时针方向旋转后得△DEC,直线AD、EB相交于点F。取BC的中点G,连接GF,则GF的最大值为_____cm。

图4
【解析】本题中因点D和点E的位置不确定,故直线AD、EB的交点F的位置也不确定。但经分析可知,直线AD、EB相交所形成的∠AFB为定值90°(证明略)。如图5,在Rt△AFB中,取斜边AB的中点O,则。由圆的概念可知,到定点的距离为定长的点在圆上,从而可得出动点F的轨迹为以AB为直径的圆。当O、G、F三点共线时,GF可取最值。如图5,点F′即为GF取最大值时点F的位置,最大值为9。

图5
【策略方法】本题涉及图形的运动,我们解决此类问题时要学会从“变化”中寻找“不变”,探寻动点在运动过程中所形成的轨迹是解决问题的关键。



