
[摘 要] 数学教学应以“促进学生的数学学习与发展”为出发点,重视学生自主学习能力的提升和数学核心素养的落实. 在实际教学中,教师应重视知识的整体关联,结合教学实际设计一些开放性、探究性的问题,引导学生经历数学知识的形成过程和建模过程,从而提升教学实效,落实学生的数学核心素养.
[关键词] 问题引领;整体建构;学习与发展;数学核心素养
学习是一个不断积累、主动建构的过程. 数学教学应打破机械“灌输”的模式,着眼于整体和全局,应引导学生关注知识之间的内在联系,从而逐步建构完善的知识结构和体系,应让学生获得对数学知识本质的理解,培养他们终身学习的能力. 笔者在教学“解直角三角形”时,通过由浅入深的问题引导学生逐层探究,彰显数学的内在联系,让学生的直观想象、数学抽象、逻辑推理等能力在联系、迁移、交流中得到了较大提升,现将教学过程整理成文,供参考,若有不足,请指正.
教学背景分析
1. 学情分析
通过前一节课的学习,学生已经知晓直角三角形中的两个锐角互余,并能灵活应用勾股定理解决相应的与边有关的问题. 本节课作为“解直角三角形”的第二课时,旨在通过对旧知的延伸与完善,让学生将边与角建立联系,从而促进思维的生长.
2. 教学目标
(1)理解和掌握解三角形的必要条件和方法;
(2)通过“割补”的方法将四边形问题转化为三角形问题,并利用解直角三角形经验解四边形;
(3)感悟转化、分类讨论、数形结合等数学思想方法的价值,优化认知结构,逐渐建立个体认知体系.
3. 教学重、难点
(1)掌握解直角三角形和解斜三角形的必要条件和方法.
(2)知识体系框架的建构及数学模型的建立.
教学过程
1. 新旧联系,激发探究欲
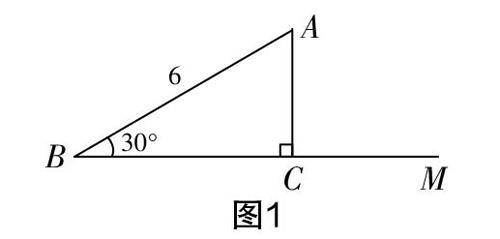
问题1:如图1所示,AB=6,∠B=30°,过点A作AC⊥BM,垂足为C. 你能解这个直角三角形吗?
追问1:解直角三角形至少需要几个条件?
预设:至少需要两个条件.
追问2:是任意两个条件都可以吗?
预设:其中一个条件必须是边.
追问3:解直角三角形时,一般涉及哪些知识和方法?
预设:勾股定理、锐角互余、锐角三角函数等.
教学说明通过旧知回顾并总结解直角三角形的相关知识与方法,为新知探究做好铺垫. 同时,通过有效追问引发学生进行深度思考,从而提升教学实效.
2. 合作探究,提炼模型
问题2:如果过点A的直线与射线BM相交但不垂直,那幺交点C可能在哪里呢?
预设:点C可能在垂足的左侧或者垂足的右侧.
教学说明通过探究点C的不同位置,实现由直角三角形到斜三角形的转化.
问题3:如图2所示,AB=6,∠B=30°,在射线BM上任取一点C,使△ABC是斜三角形. 根据现有条件,是否可以解这个斜三角形呢?如果不可以,是否可以添加一个角这一条件呢?
预设:点C在垂足的左侧时,∠A为锐角;点C在垂足的右侧时,∠A为钝角.
教学说明问题3是一个开放性问题,解决方法较多. 教学中,教师应着重引导学生进行方法梳理,使学生的思维从无序变有序,从而提高学生的思维水平. 为了计算方便,教师应启发学生添加一些特殊角,如15°,30°,45°,75°,120°,135°等.
问题4:以45°角和135°角为例,你能构造出怎样的三角形?这些斜三角形能解吗?
预设:学生通过思考与交流,得到如图3~图6所示四个斜三角形.
教学说明图3和图4是添加∠C的度数. 添加∠C的度数后,已知条件为两角与其中一个角的对边,于是过点A作射线BC的垂线便可构造两个直角三角形,而所构造的直角三角形有已知边,可以求解. 图5和图6是添加∠A的度数,已知条件为两角及夹边,于是过点C作AB的垂线,所构造的直角三角形中没有已知边,但可以设其中一条边的长为x,利用方程的思想方法来求解.
问题5:是否可以通过添加三角函数或添加边等条件来解斜三角形呢?
教学说明引导学生与添加角的方法进行类比,通过多角度分析让学生掌握解决此类问题的策略. 同时,通过经历操作、反思、类比等过程进一步体会转化、数形结合、分类讨论等思想方法,提高学生的思维水平. 在探索以上问题的过程中,教师要引导学生从特殊条件出发,如添加BC的长度为8,AC的长度为3,tanC=等条件,通过降低运算难度来提供更多思考空间,从而提升学生的解题信心.
问题6:如果只给出斜三角形三条边的长度,那幺这个斜三角形是否可解呢?例如,已知△ABC三条边的长分别为13,14,15,如何解△ABC呢?
教学说明结合以上解题经验,学生会主动构造直角三角形,通过设其中一条边为x,运用方程的思想方法分别求出所构造的直角三角形的各边,并结合三角函数求出各角的度数.
问题7:说一说你掌握了哪几种添加条件的方法,在解斜三角形的过程中分别用了哪些方法.
教学说明引导学生反思回顾,归纳解斜三角形的必要条件,体会化斜为直数学思想方法的重要价值. 在此基础上,教师可以引导学生构造“背靠式”和“叠合式”两种双直角三角形的基本模型(如图7所示),为后期的灵活应用打下坚实的基础.
3. 活学活用,巩固新知
例1:如图8所示,在四边形ABCD中,AB=6,∠B=60°,BC=8,AD=4,CD=2,∠D=135°,求四边形ABCD的面积.
教学说明四边形ABCD为一个不规则的四边形,要求出四边形ABCD的面积,需要将四边形进行“割补”,将其转化为若干个可以求解的三角形,最终计算出不规则四边形的面积. 分析发现,例1可通过分割的方法构造出如图9所示若干个直角三角形,并通过求直角三角形的面积最终求出四边形ABCD的面积.
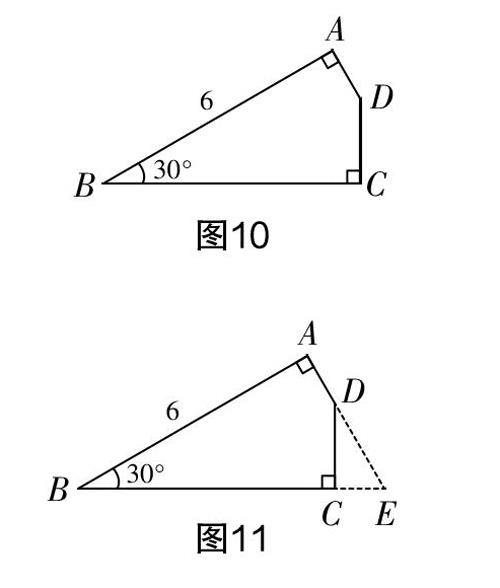
例2:如图10所示,在四边形ABCD中,AB=6,∠B=30°,∠A=∠C=90°,CD=2,求四边形ABCD的面积.
教学说明已知∠A=∠C=90°,∠B=30°,利用分割的方法会破坏这些重要的信息,从而使运算复杂化,因此,求解该题时应采用补全法,通过添加辅助线构造特殊的直角三角形,如图11所示.
在新知探究阶段,学生已经积累了丰富的解题经验,为了检测学生的知识掌握情况和思维发展水平,教师一改往日简单、机械、重复的练习,给出了更具探究性的四边形问题,引导学生通过“补全”和“分割”的方法将问题向熟悉化、简单化转化,这样既促进了新知的巩固,又让学生在逐层探究中理解了问题的本质,提高了应用水平.
4. 课堂小结,完善结构
问题8:请大家回顾本节课所学的内容,说说你有哪些收获、哪些疑惑.
教学说明该环节以小组合作交流的方式进行,让学生通过对“获”与“惑”的思考,逐步优化认知结构,建构完善的知识框架图,从而使学生的思维更加清晰化、深刻化,并提高学生的学习品质.
1. 以联系为核心,完善知识体系
在本节课教学中,教师从学生已有认知出发,通过一个开放性的图形帮助学生复习、巩固“双基”;然后引导学生改变交点C的位置,在化斜为直的转化中帮助学生积累丰富的解题经验;接着,将三角形问题拓展到四边形中,让学生通过对四边形问题的研究进一步强化对新知的理解. 在以上教学活动中,由易到难、由浅入深的探究,能让学生的思维螺旋上升,实现思维自然生长. 同时,在此过程中,教师引导学生进行知识的梳理与归纳,并带领学生感悟知识之间的内在联系,让学生逐渐将新知内化至原有知识体系中,以此逐渐完善认知体系.
2. 以问题为主线,提高教学效率
教学中,教师精心研究教学、研究学生,以学生已有认知为起点,以发展学生为目标,结合教学设计精心设计问题,让学生在问题的解决中积累学习经验,提炼数学思想方法,提高教学有效性. 本节课以直角三角形为载体,通过由浅入深的问题激发了不同层次学生的探究欲,使学生的思维更活跃,课堂更高效.
3. 以学生为主体,提升学习能力
在本节课教学中,教师以问题为主线引导学生积极探究,充分调动了学生参与课堂的积极性,发挥了学生的主体性,提高了学生的自主探究能力. 例如,在解斜三角形的过程中,教师先启发学生添加一个角,然后引导学生运用类比添加边、三角函数等条件,使学生的思维不断纵深,从而提升学习能力.
总之,在课堂教学中,教师要少一些“灌输”,要引导学生通过自主探究发现数学的本质,感受数学思想方法的魅力,提升学生的数学建模能力,落实学生的数学核心素养.
作者简介:郑燕穗(1981—),本科学历,中学高级教师,从事初中数学教学与研究工作,广东省中小学“百千万人才培养工程”初中理科名教师,汕尾市中小学名教师工作室主持人.



