吴微微 徐延林 何 艳
国防科技大学电子科学学院 湖南长沙 410073
一、概述
麦克斯韦以一种近乎完美的方式统一了电和磁,形成一门独立的学科——电磁学。同时,预言了电磁波的存在,这是物理学家在统一之路上的巨大进步。若从微观角度探究电磁场的特性,需将宏观中的有向曲线、有向曲面以及由封闭曲面围成的体积无限缩小至趋于零的程度,用电磁场的散度和旋度等物理量代替宏观中的通量、环量等物理量进行研究。标量场的梯度、矢量场的散度及其旋度的计算离不开符号简化史上一个奇迹——哈密顿算子(∇算子)。教学实施过程中发现,当从宏观角度转向微观角度探究电磁场特性时,学生们理解起来有不小的难度。例如,在电磁场理论中,如何理解自带方向的哈密顿算子的物理意义?除了用于计算,梯度、散度和旋度的物理意义是什幺?本文将通过三个模型,详细阐释哈密顿算子、梯度、散度和旋度的物理意义,便于学生掌握微分形式麦克斯韦方程组的核心内容。
二、哈密顿算子的解读
为了简化电磁场理论中的运算,英国数学家、物理学家和力学家威廉·罗恩·哈密顿引出了倒三角符号∇,因此得名哈密顿算子,它是场论分析中不可或缺的工具。它是一个同时具有矢量和微分双重特性的矢量算子,主要研究场量在空间中的变化。要理解哈密顿算子,需要从描述函数f变化快慢的概念——导数说起。当函数f的变化与时间有关,则记为f(t)。描述该函数增量与自变量—时间增量之间比值的函数为g(t)=Δf(t)/Δt。例如,当f(t)为距离时,则g(t)为速度;当f(t)为速度时,g(t)为加速度。当f(t)为一条随时间变化的曲线时,f(t)的增量Δf(t)与其微分df(t)之间的关系如图1所示。
图1中,时间轴上的增量为Δt,其微分为dt,两者大小相等。增量Δy表示时间上增加Δt时函数f(t)的增量,它是函数f(t)的实际变化量Δf(t)=Δy。当在P点做一条切线,以直线代替曲线,则当时间轴上变化了Δt,直线上对应
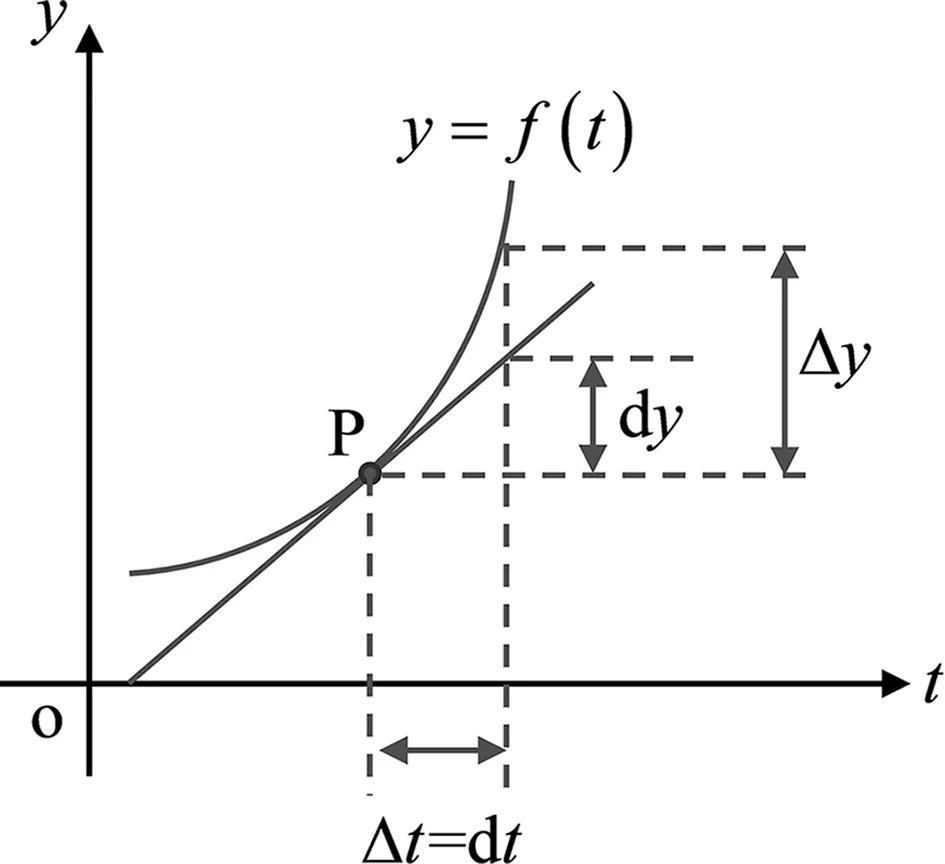
图1 函数f(t)的增量Δy与微分dy的关系
的变化即为微分df(t)=dy,微分dy为增量Δy的线性主部。这种“以直(dy)代曲Δy”是现代微积分的一个核心思想,利用P点处的导数dy/dt就可以表示该点处函数随时间变化的快慢。若想研究该函数f(t)在空间中某一点上随空间变化的快慢,需首先选择一个坐标系并进行研究。为简单起见,本文选择直角坐标系进行研究,诠释哈密顿算子的物理意义。将函数f(t)的自变量由时间变量t改为直角坐标系中任意一个轴向,如x轴,则导数dy/dx研究的是函数y=f(x)在空间中沿x轴方向的变化率。若想同时研究P(x0,y0,z0)点处,函数f(x,y,z)沿三个坐标轴方向的空间变化率,则需利用偏导数分别研究各个方向上的空间变化率。首先,固定该点在y轴和z轴上的位置y=y0和z=z0,研究函数f(x,y0,z0)沿x轴方向的变化率:
(1)
同理,可得到沿另外两个方向的变化率。若想同时表示空间P(x0,y0,z0)点在三个坐标轴方向上的空间变化率,则需将三个方向上的变化率分别用相对应的单位矢量进行标记后相加即可。
但由于将三个方向上的变化率用类似公式(1)的方式表示出来时,虽然概念清晰,但十分冗长。于是,哈密顿提出一种矢量算子简化上述表示式,得到如下简洁形式:
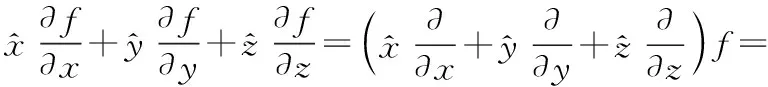
(2)
综上所述,哈密顿算子的物理意义是研究一个空间分布函数f(x,y,z),沿三个坐标轴方向各自的空间变化率。
三、梯度模型
在电磁场理论中,标量场的梯度和矢量场的散度及旋度的物理意义一直是教学的重点和难点。基于上一小节阐释哈密顿算子物理意义的过程,用于研究标量场的梯度的物理意义跃然纸上。设标量场函数f(x,y)的空间自变量为x和y,如图2所示。在空间位置点P(x0,y0)处的梯度表明了该函数f(x,y)在此点处沿x和y方向增加率最快最大的方向,由图2中箭头所示。图3为函数f(x,y)投影到xoy平面上的情况。
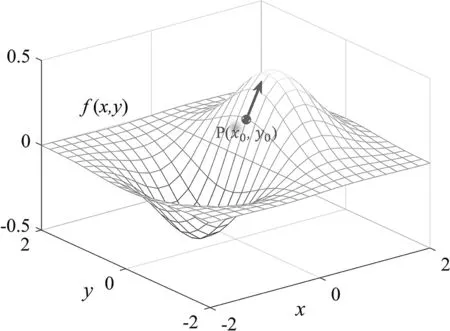
图2 标量场的梯度
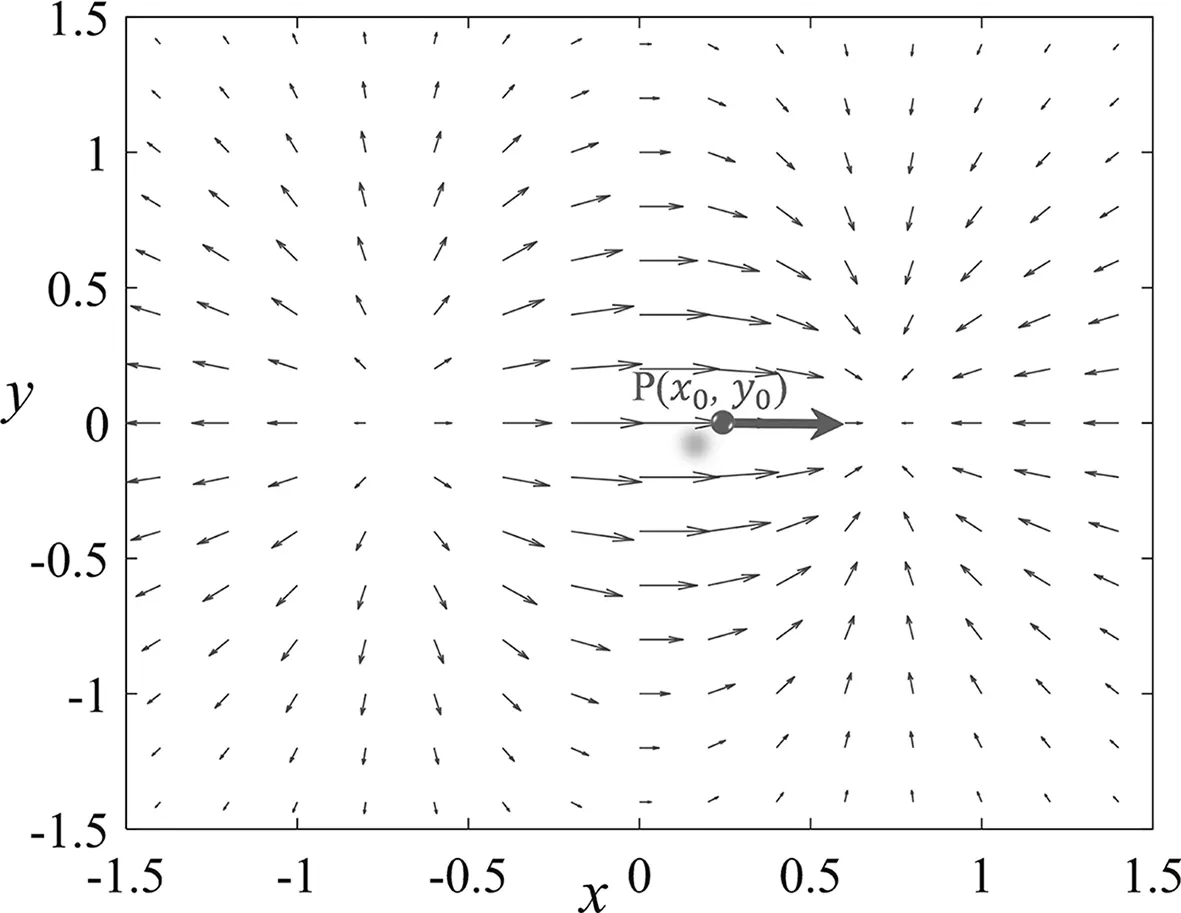
图3 标量场及其梯度的二维投影
四、散度模型
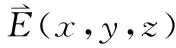
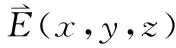
(3)
若梯度研究一个标量场在空间某一点的变化,散度则研究一个具有不同极化方向的矢量场在空间某一点的变化,但矢量场的每一个分量实则为一个标量场。比如,Ex(x,y,z)、Ey(x,y,z)和Ez(x,y,z)均是标量场。这里的物理概念学生容易混淆,容易把场量的下角标表示的极化方向和括号里表示空间分布的自变量发生混淆。这是一个教学重点和难点,需要结合物理模型进行阐释、强调和区分。
(4)
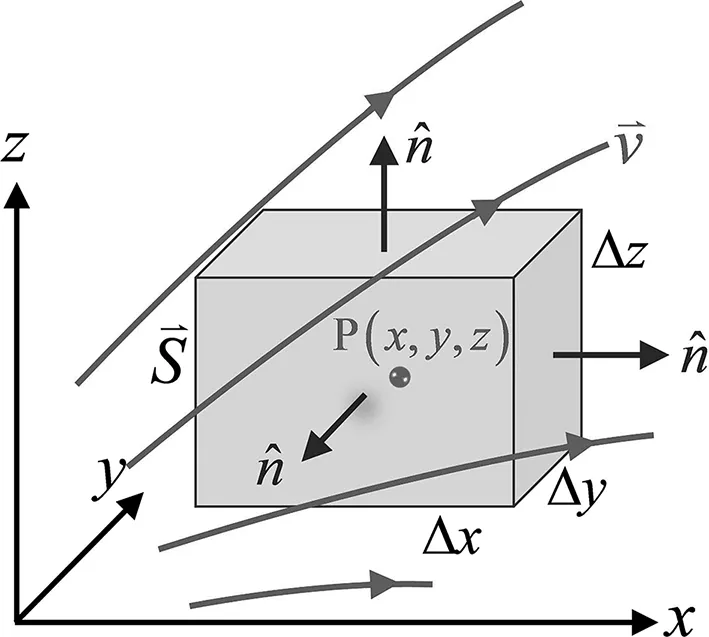
图4 研究散度的流速场模型
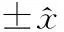
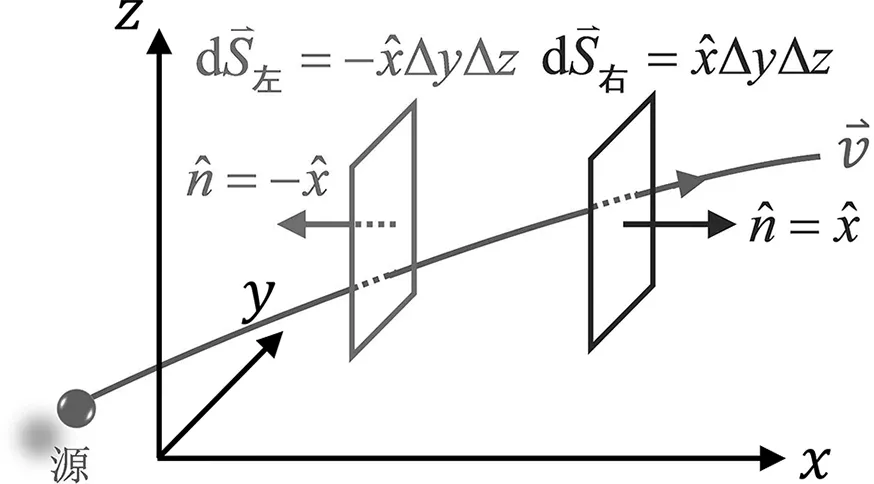
图5 流速场的源在封闭曲面外部
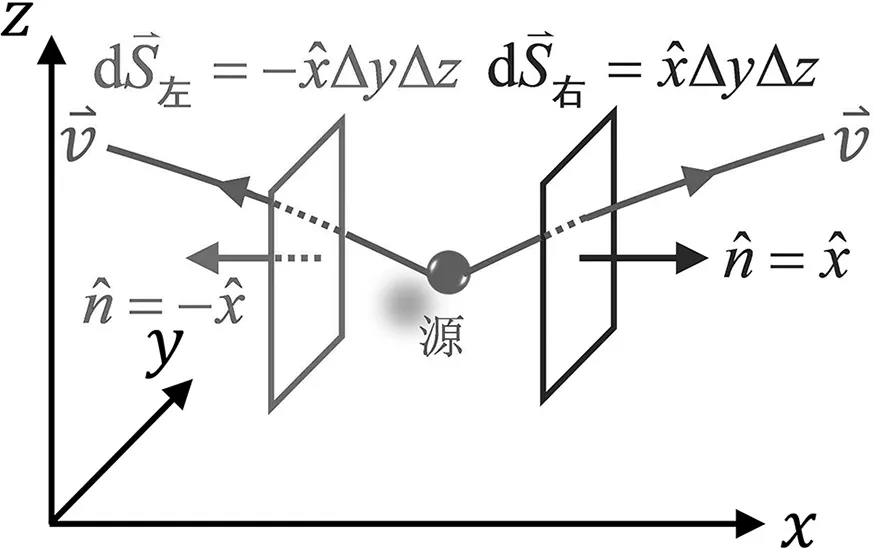
图6 流速场的源在封闭曲面内部
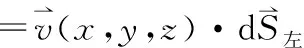
=-vx(x,y,z)ΔyΔz
(5)
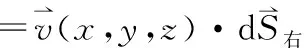
=vx(x,y,z)ΔyΔz
(6)
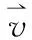
ψ总=ψ左+ψ右+ψ前+ψ后+ψ下+ψ上
=-vx(x,y,z)ΔyΔz+vx(x,y,z)ΔyΔz
-vy(x,y,z)ΔxΔz+vy(x,y,z)ΔxΔz
-vz(x,y,z)ΔxΔy+vz(x,y,z)ΔxΔy
=0
(7)
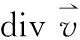
(8)
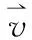
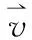
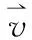
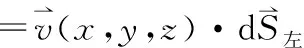
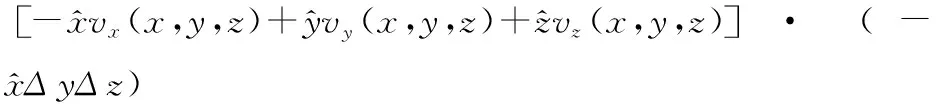
=vx(x,y,z)ΔyΔz
(9)
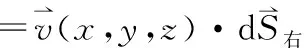
=vx(x,y,z)ΔyΔz
(10)

同理,可用同样的方法求出其他四个面上的通量:
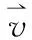
(11)
通过研究通量或散度来了解其通量源的特性,可避免直接研究通量源。利用横截面上截获的通量获取截面内场源的大小是一种研究矢量场源的方式。
五、旋度模型

电磁场理论中,一个矢量场的旋度一直是一个教学难点。为便于学生理解,在此用一个简单的旋度计模型来阐释其原理,如图7所示。
图7中不导电圆盘在xoy平面上。圆盘上沿x轴和y轴方向用两根不导电细棍固定四个带相同正电荷量的小球A、B、C和D,这个沿xoy平面的结构可自由转动。它通过一段弹力线与沿z轴放置的一根不导电圆柱相连。该圆柱固定不动。四个小球受到电场力E左、E右、E前和E后的作用,如图8所示。
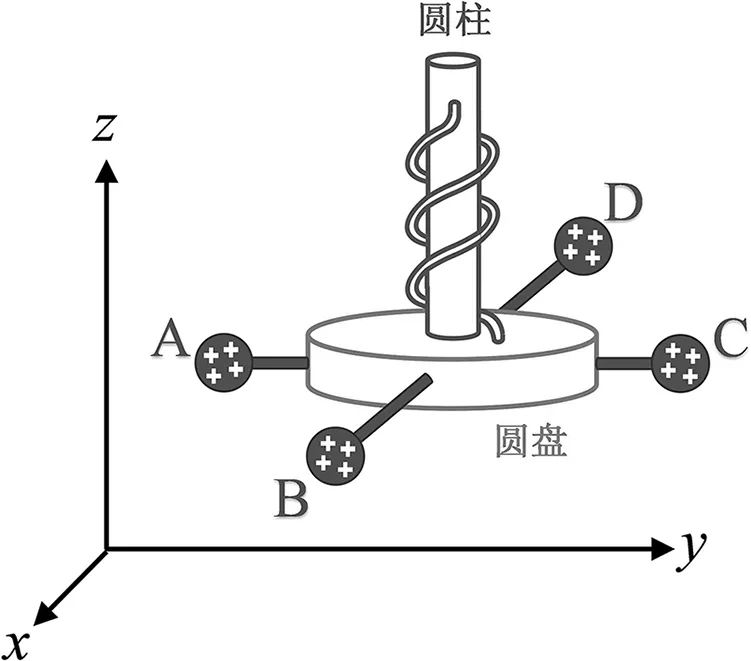
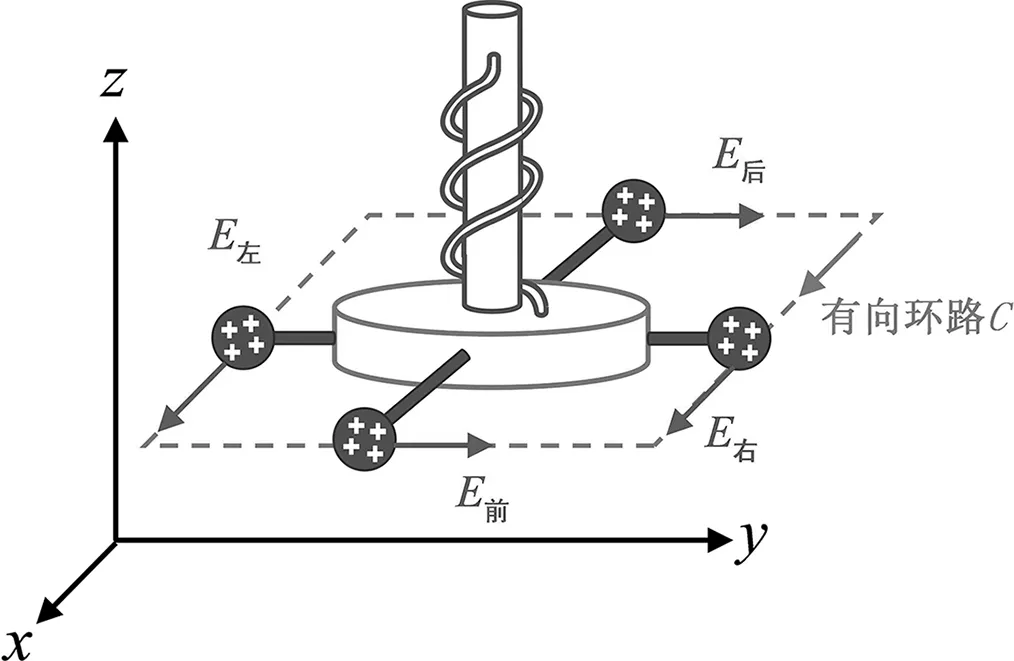
图7 旋度计模型图 图8 带电小球所受电场力
其中,有向环路C的方向为顺时针方向。电场力E左和E右沿x轴方向,E前和E后沿y轴方向,在此研究沿一个方向的两个电场力的效果足以说明问题。
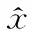
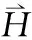

(12)

(13)
(14)
(15)

(16)

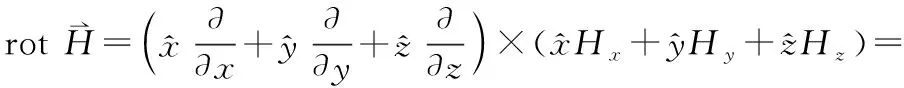
(17)
更多具体表示式可参见教材[2],在此,可利用“旋度计”模型深入理解旋度的概念。
结语
本论文针对教学中的重点和难点——哈密顿算子、梯度、散度和旋度,利用图形和模型进行详细阐释。讲解哈密顿算子的时候,首先让学生回顾时间轴上导函数的定义,再过渡到空间上的导函数。讲解标量场的梯度时,利用二维坐标系和三维坐标系视角进行诠释。讲解散度时,利用流速场模型进行类比。讲解旋度时,利用“旋度计”模型辅助学生理解。与此同时,还诠释了空间矢量场的下角标和自变量的物理意义。教学实践表明,本文对“电磁场与电磁波”系列课程中这部分内容的授课很有帮助。



