何 峰,杨 松,任天娇,卞红杰,付恩越
(辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)
超静定梁理论一直是结构分析中非常重要的一部分,对其解析解的获取也是工程界和学术界不断探索的内容。而两端固定、受均布载荷梁的平面应力解由Ding HJ 等[1]获得;戴瑛[2]分析了两端固定受均布载荷短梁的平面应力解,改进简化了边界条件,并通过数值方法验证了其解的准确度;张劲夫[3]应用瑞利-里兹法近似求得考虑固定端轴向约束力影响下的解析解并得到固定端梁的挠曲线函数和挠曲线形状;王敏中[4]利用最小二乘法,对固定端采用位移平方为最小的边界条件;邢静忠[5]将Maple 引入力学教学,引导和培养学生利用数学工具的习惯和能力,强化算法设计和程序的通用性和灵活性,为处理复杂问题提供帮助;陈小亮[6]等利用Maple 软件探索了弹性力学应力函数逆解法的计算机求解规范流程;卢小雨[7]等利用Maple 来求解弹性力学中的一些具体问题。
文章基于Maple 强大的符号运算能力,针对已验证均布载荷作用下两端固定等截面梁应力函数有效性的前提下,结合弹性力学逆解法思想,编制Maple 程序,修正了文献[2]解析解,应用得到精确解析解与文献[3]和有限元模拟结果进行精度的对比。
1 单跨三次超静定梁弯曲问题
考虑单位厚度、矩形截面的梁,两端固定,梁的上表面受均布载荷q的作用,下表面不受力,梁跨长为l,梁的高度为h,体力不计,如图1 所示。
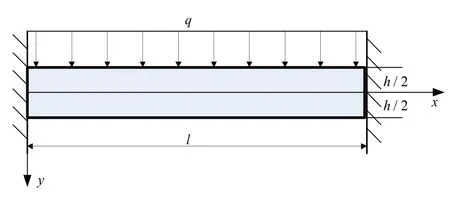
图1 均布载荷作用单跨三次超静定梁[1-3]
依据文献[1-2]中采用的重调和应力函数U为7 项五次多项式,并验证了其准确度:
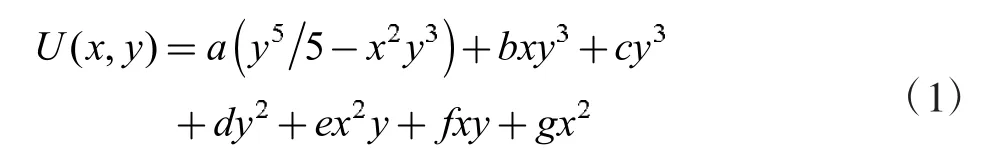
式中:a,b,c,d,e,f,g是7 个待定系数,由边界条件来确定。
2 弹性力学逆解法与Maple 求解
弹性力学逆解法思想:
(1)给出满足条件的应力函数;(2)验证应力函数是否满足相容方程;(3)根据应力函数和应力分量关系式求解应力分量;(4)结合几何方程和物理方程,求解位移分量;(5)最后根据边界条件列出方程求出待定系数,最终得到应力分量和位移分量。
Maple 程序实现如下:
(1)输入应力函数
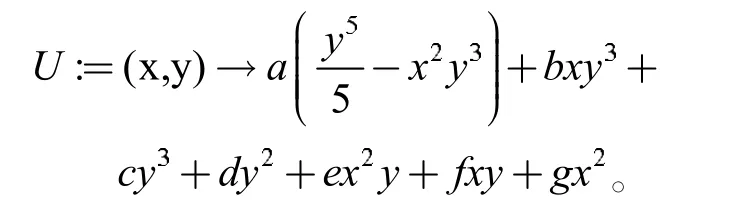
(2)验证是否满足相容方程,经验证该等式为0,所以满足相容方程。
equ0:=diff(U,x$4)+2*diff(U,x$2,y$2)+diff(U,y$4)结果为0。
(3)求应力分量
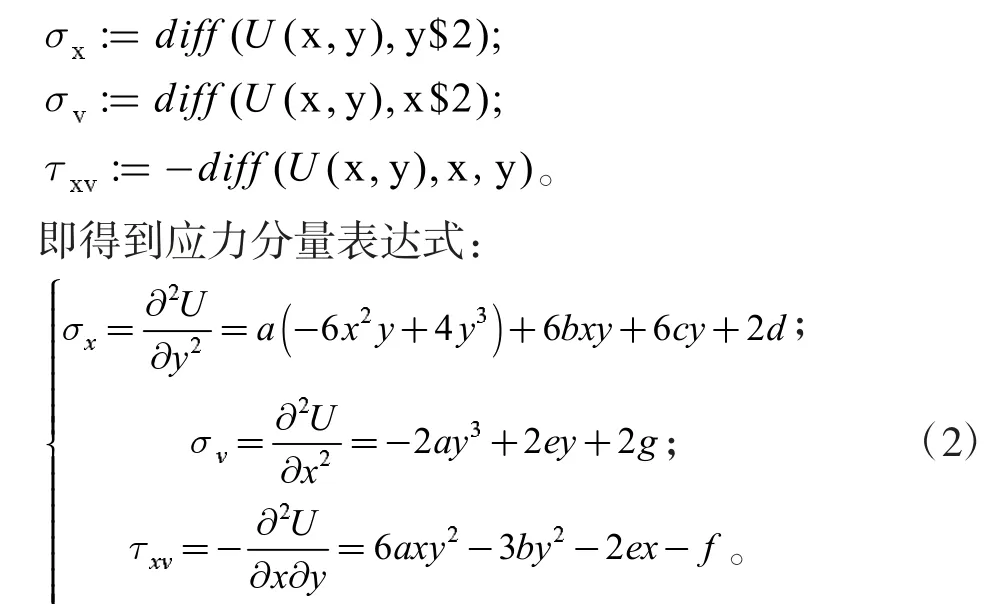
(4)求位移分量
根据几何方程和物理方程,建立偏微分方程组并求解位移分量。
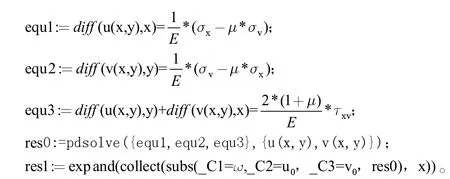
为了符合弹性力学位移分量表示方式,再对其积分常数进行变换,Maple 程序最终得到位移分量并经简化整理表达式如下:
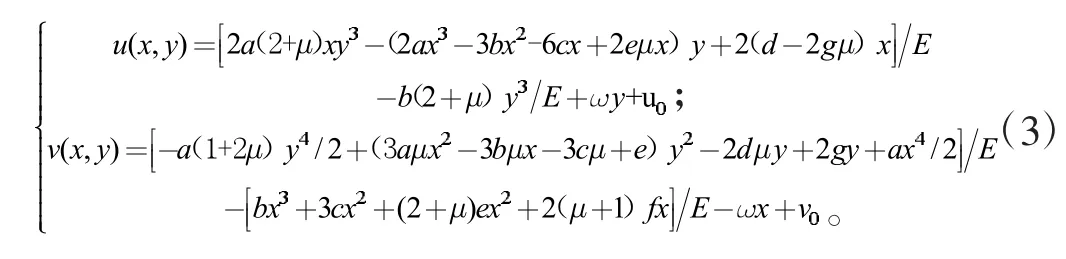
而文献[2]位移分量表达式为
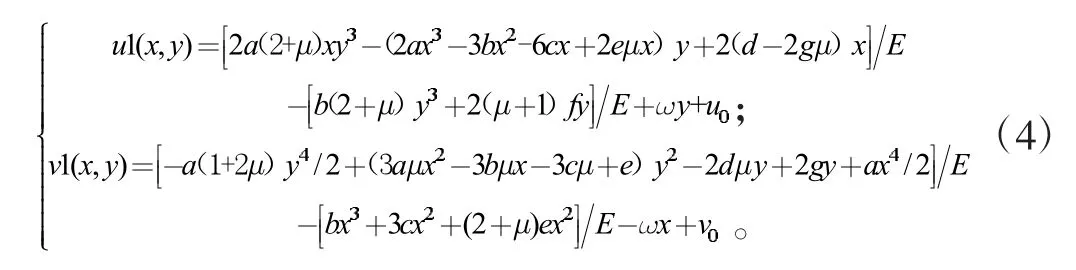
通过Maple 程序求解结果与文献[2]对比可知文献[2]水平位移分量多了一项2(1+μ)fy,竖向位移分量少了一项2(1+μ)fx,所以导致文献[2]求解结果误差大。其中:ω,u0,v0为积分常数,由位移边界条件确定。
(5)边界条件
细长梁固支边界条件根据文献[1-2]的表示方法,边界条件为如下形式:
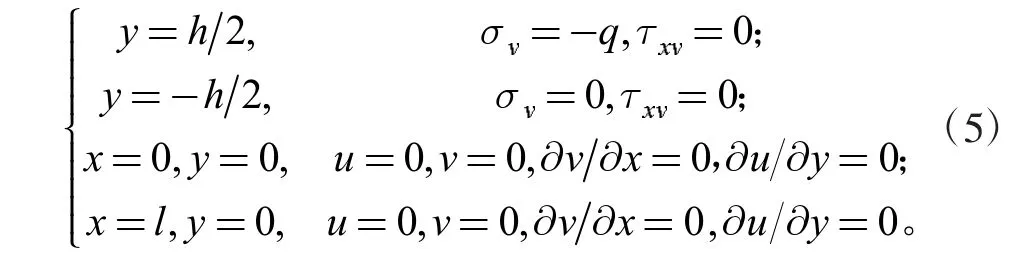
由于Maple 程序求解位移为方程组,为方便程序求解令U1:=u(x,y);V1:=v(x,y);根据边界条件式(5)Maple程序如下:
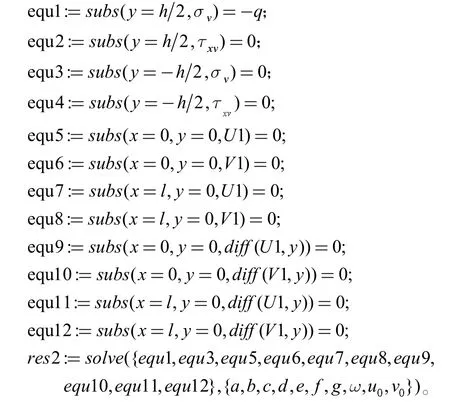
由边界条件(5)式得到12 个方程(其中y=±h/2,τxy=0边界条件列出的方程非独立,有效方程10 个),最终确定的7 个系数和3 个积分常数分别为
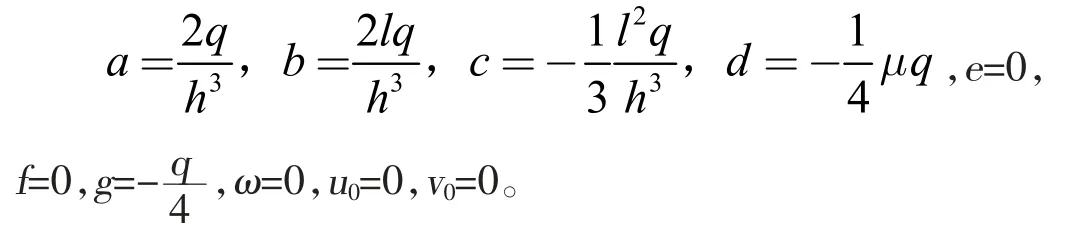
(6)应力分量和位移分量
按边界条件(5)式,编制Maple 计算程序如下:
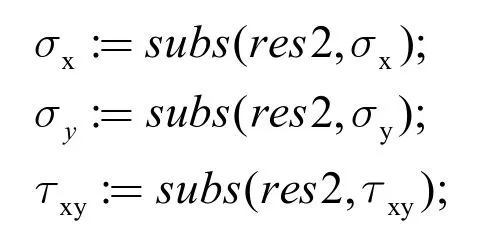

3 应用分析
设梁力学及几何参数如下:载荷集度q=50N/m,弹性模量E=2.0lel1Pa,泊松比为μ=0.3;长度l=1m,横截面积S=6e-5m2;宽度为0.02m,高度为0.003m,截面惯性矩Iz=4.5e-11m4。
3.1 有限元模拟
结合有限元法优点,其可以对固定端边界面上的所有节点施加位移为零的约束,并随着节点数目的增多,可以无限接近固定端真实的位移边界,因而有限元结果常作为理论解近似程度的比较依据;通过建立两端固定梁的有限元模型,其网格数69,节点数139;边界及施加载荷见图2;最终模拟得到梁的最大挠度:vmax=0.000325m。
3.2 文献[3]Maple 程序实现及梁轴线挠曲线
依据文献[3]应用瑞利-里兹法近似求得考虑固定端轴向约束力影响下的解析解Maple 程序如下:
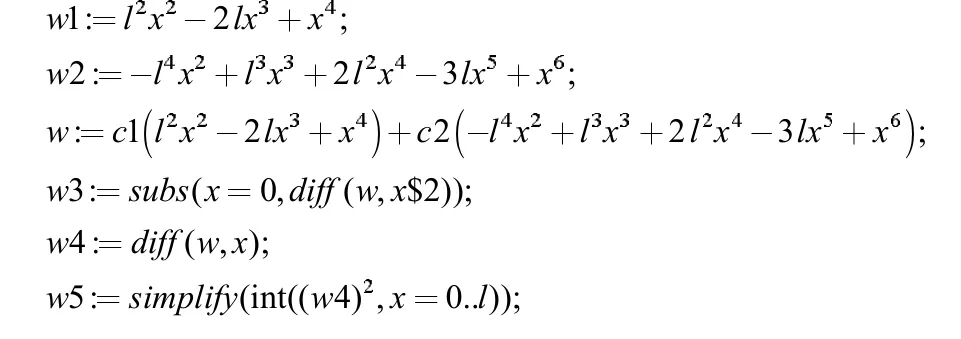
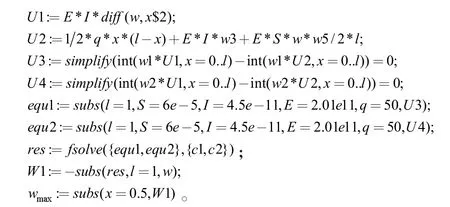
通过运行以上Maple 程序得到梁轴线挠度方程、挠曲线见图3 及中点处的挠度如下:
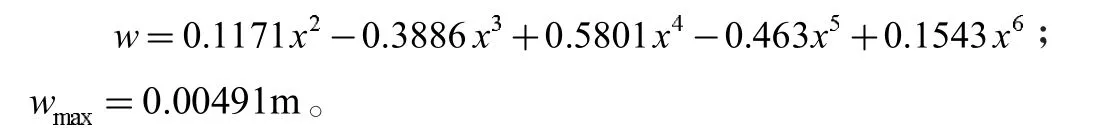
3.3 论文梁轴线挠度方程及挠曲线
依据前文位移分量表达式(7)及梁的参数,Maple 程序如下:

(4)小结
通过有限元模拟得到最大挠度为0.000325m、论文及文献[3]梁轴线中点处最大挠度分别为0.000576m 和0.00491m;根据算例结果及图3-4 梁挠曲线形态可知,论文解析解结果与有限元模拟结果为同一数量级,且更加逼近真实结果。而文献[3]结果与论文和有限元结果相差一个数量级,其原因为文献[3]采用了材料力学中挠曲线近似微分方程,其中忽略了剪力对梁变形的影响和转角前提得到的。
4 结论
(1)基于文献[1-2]对两端固定梁受均布载荷作用下应力函数形式已经验证准确性的前提下,应用弹性力学逆解法思想,编制Maple 计算程序,对文献[2]解析解进行了修正,得到了均布载荷作用单跨三次超静定梁精确的应力分量和位移分量表达式。
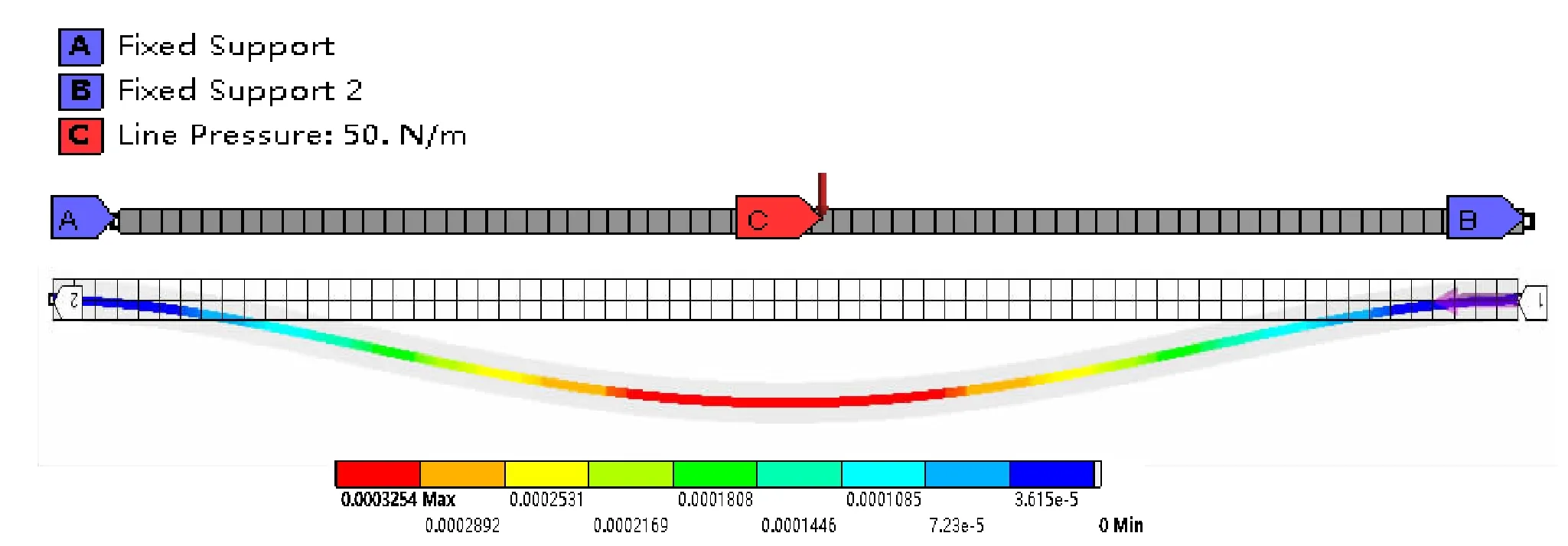
图2 两端固定受均布载荷作用的梁有限元模拟
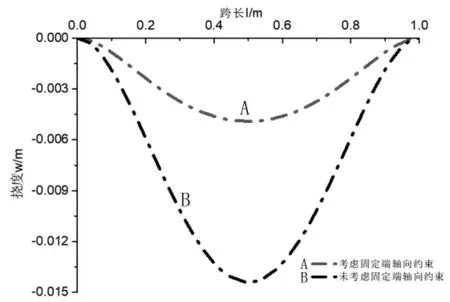
图3 文献[3]梁的挠曲线
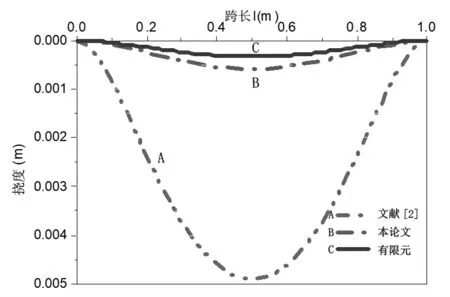
图4 两端固定受均布载荷作用的梁挠曲线
(2)结合具体算例,通过有限元模拟与论文解析解对比,得到均布载荷作用单跨三次超静定梁挠曲线和中点处最大挠度同处一个数量级,并对文献[3]编制Maple 计算程序,验证了其结果的准确性,得到的梁中点的最大挠度与论文结果相差一个数量级,进一步证明了采用弹性力学方法解决相似问题的精确性。



