例谈从特殊到一般的数学思想在解题中的妙用

浙江省宁海县桃源初级中学 陈静雯

数学思想的学习不仅在数学解题中有帮助，同时在生活中也有着很大的用处。数学思想非常丰富，本文通过一堂自己的课堂实录，谈谈从特殊到一般的数学思想在解题中的妙用。

例题：将一块半径足够长的扇形纸板的圆心放在面积为S的正n边形的中心O点处，并将纸板绕点O旋转，当圆心角为时，正n边形被重合部分的面积为_____。

题目分析：此题没有图形，而且是抽象的n边形，图形也不容易画出，所以重合的图形同样也都不明确，整体给学生的感觉就是摸不着头脑，不知道从哪里切入题目。

一、从特殊到一般，引导学生由浅入深

1.如图1，将一块半径足够长的扇形纸板的圆心放在面积为S的等边△ABC的中心点O处，并将纸板绕点O旋转，当圆心角为120°时，等边△ABC被重合部分的面积为_____。

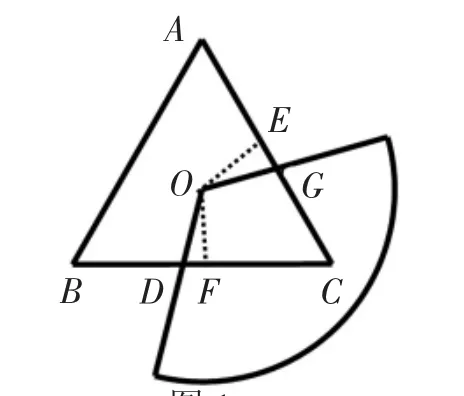
图1

分析：过点O作OE⊥AC，OF⊥BC分别交于点E，F.

易得∠EOF=120°

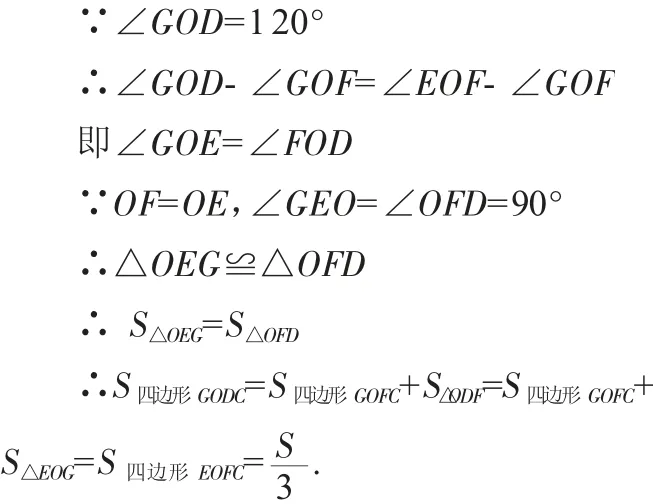
设计意图：在教学过程中，可以借助几何画板，结合“计算工具”，演示出重合面积始终是一个固定的值，使枯燥复杂的数学知识变得立体直观，激发学生的兴趣。几何画板演示出重合部分的位置在不断改变，为什幺重合部分的面积却始终不变呢？这个固定的值是多少呢？如何来证明呢？一系列的疑问激发学生探究问题的兴趣和热情，从而产生强烈的求知欲。

2.如图2，将一块半径足够长的扇形纸板的圆心放在面积为S的正方形的中心O点处，并将纸板绕点O旋转，当圆心角为90°时，正方形被重合部分的面积为_____。

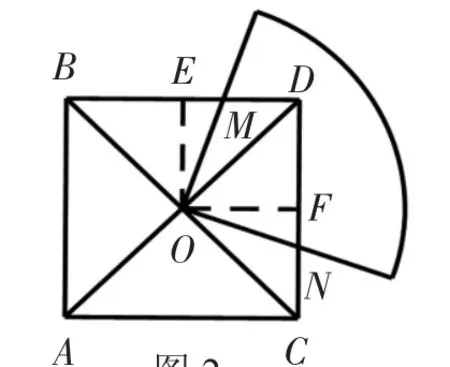
图2

分析：过点O作OE⊥BD，OF⊥CD分别交于点E，F.

易得∠EOF=90°

∵∠MON=90°

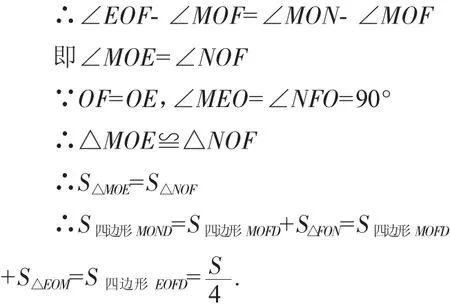
设计意图：经过第一题的探索，学生已经了解了解题思路及解题方式，借助多媒体激发了学生的兴趣，所以接下来的自主探索就水到渠成了。

此时的学生对自己的猜测更加肯定了，离最后的成功越来越近，学生探索的兴趣则更加浓厚。

3.如图3，将一块半径足够长的扇形纸板的圆心放在面积为S的正五边形的中心O点处，并将纸板绕点O旋转，当圆心角为72°时，正五边形被重合部分的面积为_____

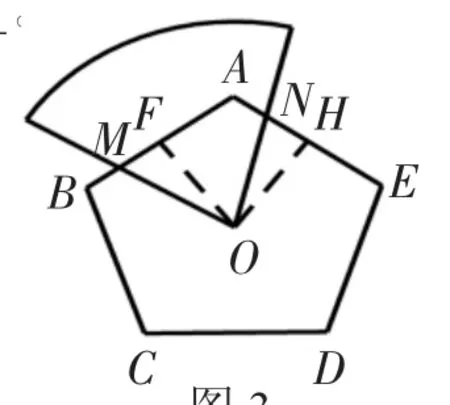
图3

分析：过点O作OH⊥AE，OF⊥AB分别交于点H，F.

易得∠HOF=72°

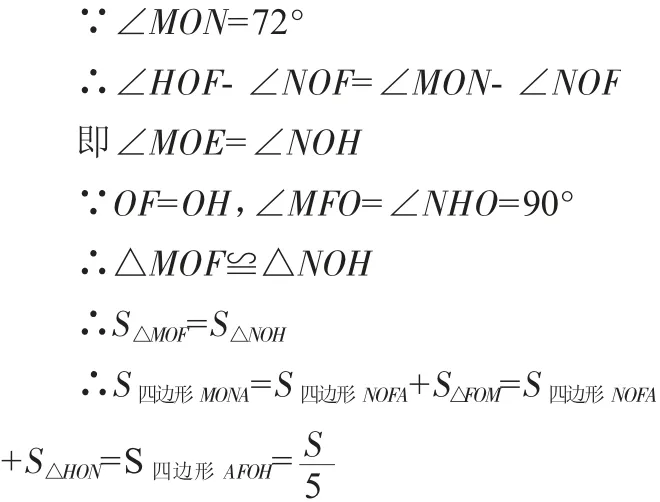
再次借助几何画板，让学生感受到面积的不变，然后定格在如图4的位置，让学生体会面积的转移。

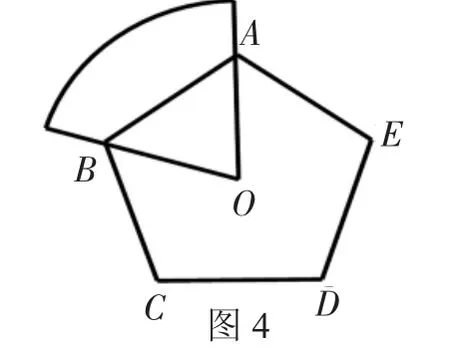
根据以上正三角形、正方形、正五边形的探究过程，请学生得出合理的结论。

从特殊到一般的推广：将一块半径足够长的扇形纸板的圆心放在面积为S的正n边形的中心O点处，并将纸板绕点O旋转，当圆心角为时，正n边形被重合部分的面积为。

借着学生得到结论后成功的喜悦和探索兴趣正浓，教师要引导学生发散思维：“类似地，我们还可以探索怎样的问题呢？”

二、变更问题，引导学生应用思想

学生很自然地能提出问题：面积为S的全等的正n边形纸板，其中一个正n边形纸板的顶点与另一个正n边形纸板的中心O重合，并将纸板绕点O旋转，当重合部分的中心角度为时，两个正n边形重合部分的面积为____。

此时教师可以充分利用小组合作讨论所带来的无穷智慧，把探索的课堂给学生，还可以进行组内交流，也可派代表进行组际交流，交流猜想结论，交流验证方法等等，充分发表自己的看法，形成小组集体意见。同样由学生概括两个正n边形被重合部分的一般规律。

学生讨论发现当n=3时，旋转过程中重合部分的面积不是一个定值（至于这个变化的面积是否也有规律让学生课后思考），只有当n＞3时，这个重合部分面积才是定值。

如图5，面积为S的全等的正方形纸板，其中一个正方形纸板的顶点与另一个正方形纸板的中心O重合，并将纸板绕点O旋转，当重合部分的中心角度为90°时，两个正方形重合部分的面积为____。

在这两轮的探索中，让学生体会数学从一般到特殊、类比的数学思想，教学过程中涉及了变更问题、尝试猜想、总结归纳等教学环节，为学生构建研究平台，鼓励学生自主动手实践。

三、反思小结，引导学生提炼思想

反思是数学活动的核心和动力，所以在探究学习中，教师应该引导学生进行反思与小结，并及时提炼上升到数学思想的高度，让学生掌握探究的方法，培养学生探索解决问题的能力。可以采用问题串的引导方式，例如：

1.问题开始，我们是怎样入手的？（从正三角形、正方形、正五边形到正n边形）

2.在证明过程中我们主要运用了哪些方法？（证明三角形全等将面积转移）

3.在探究中运用了哪些数学思想方法？（从特殊到一般、类比思想、转化思想等等）

四、变式拓展，引导学生发散思维

学以致用，那就让学生应用上面学习的方法和结论，尝试解决下面的问题。

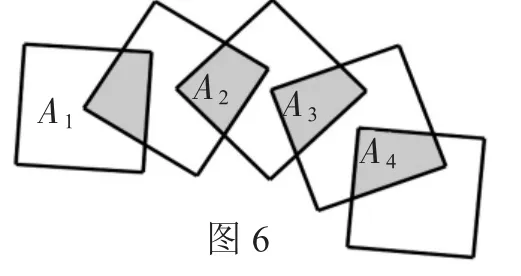
变式一：如图6，将n个边长都是1cm的正方形按如图所示摆放，点A1、A2、…、An分别是正方形的中心，则n个这样的正方形重叠部分的面积和为（）。

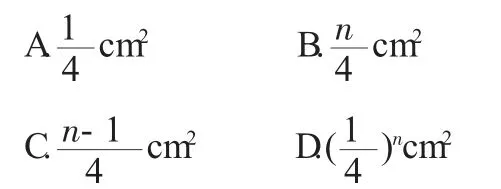
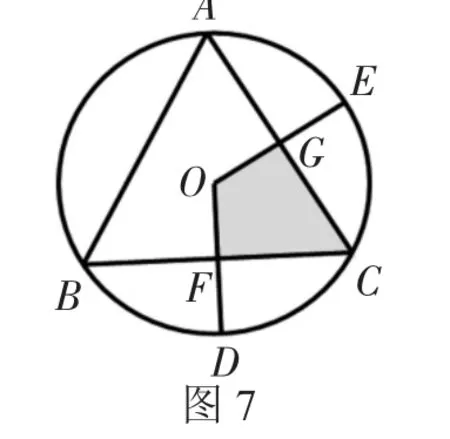
变式二：⊙O是等边三角形ABC的外接圆，OD、OE是⊙O的半径。

如图7，当OD⊥BC于点F，OE⊥AC于点G，求证：阴影部分四边形OFCG的面积是△ABC面积的.

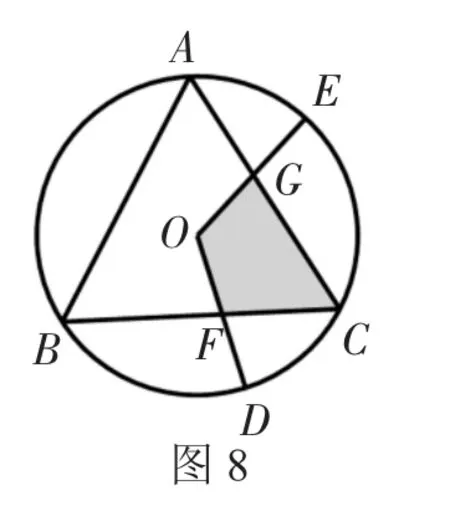
如图8，若∠DOE保持120°角度不变，求证：当∠DOE绕着O点旋转时，由两条半径和△ABC的两条边围成的图形（图中阴影部分）面积始终是△ABC的面积的.

分析：由对称性很容易就可以得到四边形OFCG的面积是△ABC的面积的。

只要保持∠DOE保持120°角度不变，这个阴影的面积也保持不变，它等于四边形OFCG的面积，即是△ABC的面积的.

变式三：如图9，已知点A，B，C是半径长为2的半圆O上的三个点，其中点A是弧BC的中点，连接AB，AC，点D，E分别在弦AB，AC上，且满足AD=CE，连接OD，OE，若∠BAC=120°，当点D在弦AB上运动时，四边形ADOE的面积是否变化？若变化，请简述理由；若不变化，请求出四边形ADOE的面积.

图9

∴四边形ADOE的面积不变

变式四：如图10，矩形ABCD中，AB=4，AD=6，O为矩形ABCD的中心，将直角三角形的直角顶点与O重合，一条直角边OP与OA重合，使三角板沿逆时针方向绕点O旋转，两条直角边始终与边AB、BC相交于N、M，AN=y，BM=x,则y与x之间的函数关系式为________。

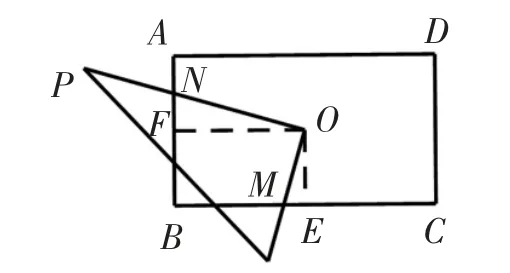
图10

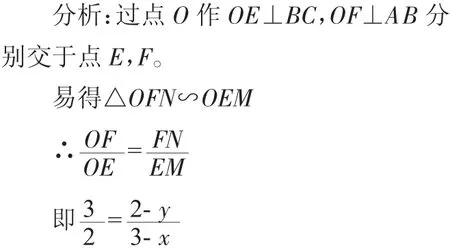
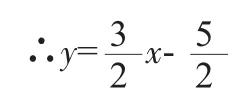
设计意图：采用变式拓展，围绕同一图形，变换旋转角度，有利于学生更扎实地掌握知识结论。

结束语

学生经过自主探索、实践，发现归纳结论，这是对学生主动参与精神的激励，在过程中能使学生掌握数学思想和解题技巧，体会到主动探索成功后的喜悦，增强学生主动学习的动力和信心。而数学学习是一个长久的过程，不仅在平时的课堂中，而且也在解题中。数学思想的掌握必有利于今后的学习和生活，因此在今后的教学过程中，教师应该倡导学生数学思想的掌握，而不是教会学生模仿和记忆。