■袁绍建
识别“形异质同”,引发教学思考
■袁绍建
初中数学教师大多热衷解题研究,特别是对解法技巧、题型归类的研究热情很高。如果能更进一步,从形式走向本质,识别出更多“形异质同”的考题,并将其有效关联,研发成复习课例,便可促进解题研究转化为有效的“生产力”,从而服务解题教学。
解题研究 形异质同 思路突破 教学思考
解题研究是很多同行的兴趣,尤其是研究一题多解,有些解题研究能化繁为简,揭示问题的深层结构,对我们深刻理解考题是十分有益的。然而,如果解题研究只是止步于一题多解,或多解归一,不能从形式走向本质,还是没有让解题研究转化为“生产力”。本文结合笔者近期关注到的两道同类考题,浅谈对同类考题的解题研究与教学思考。
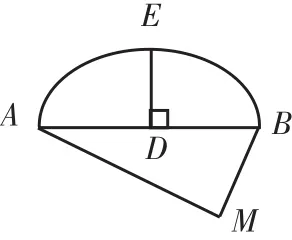
图1
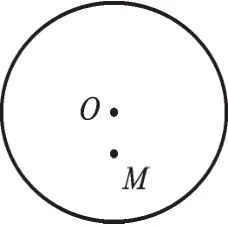
图2
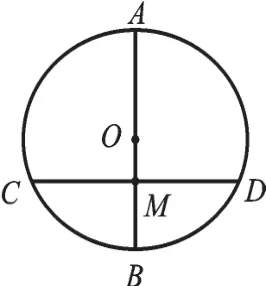
图3
一、同类考题及思路突破
考题1(2017·陕西第25题节选)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图1所示。管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又要能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌),同时,再合理设计好喷灌龙头喷水的射程就可以了。如图1,已测出AB=24 m,MB=10 m,△
问题解析:这是一道生活情境问题,为了解决王师傅的喷灌龙头的射程问题,需要将其抽象成几何图形中求最值的问题,即在图1中,点M到图形中哪一个点的距离最大。目测似乎是AM的长最大,但这种“直觉”往往会误导我们,我们还需要考虑点在劣弧AB上的情况,并且要经过计算再进行比较。
性质回顾:我们先回顾“圆”的一个常见性质,如图2,若点M是圆O内一点,则过点M的最长弦、最短弦在哪儿?显然,如图3,我们可先作直线OM得出直径AB,再过M作CD⊥AB,交圆O于C、D,则所求的最长弦即直径AB,最短弦即为CD。AMB的面积为96 m2;过弦AB的中点D作DE⊥AB交︵AB于点E,又测得DE=8m。请你根据以上提供的信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
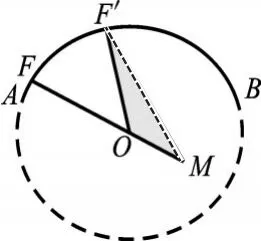
图4

图5
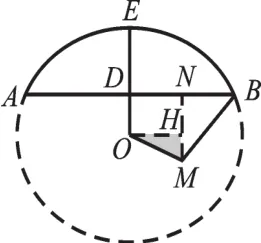
图6
思路突破:如图4,设劣弧AB的圆心为O,寻找点M到圆的最远距离应该作射线MO交劣弧AB于F点。接下来要解决两个难点,一是劣弧AB的半径以及OM的长。于是构造图5,在图5中,利用垂径定理,可得AD=12,在 Rt△AOD中,AO2=122+(AO-8)2,解得:OA=13。构造图6进一步求出OM的长,过点M作MN⊥AB,垂足为N,过O作OH⊥MN,垂足为H。由S△ABM=96,AB=24,可得MN=8,NB=6,AN=18,相应的MH=3,于是在Rt△OMH中,OM=︵==3,结合上面已求出AB的半径为13,MF=OM+r=35+13≈19.71(m)。
如果就这样给出答案还不够严谨,因为缺少对圆心O是否在△AMB内部的分析。
如图7,设直线EO交AM于C点,

图7
由CD∥MN,可得△ADC∽△ANM,,显然OD<CD,即点O在△AMB内部,即上面求得的MF为草坪上的点到M点的最大距离。当然,我们还可在图7中计算出AM的长为297,将其与最大值MF(35+13)比较后,也可发现AM<MF,从而确认解答。
考题2(2017·江苏某县模考卷第28题)如图8,平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(-3,0)两点,与y轴的负半轴交于点C,且OA∶OC=1∶3。(1)求a,b,c的值;(2)过点B作线段BC的垂线交抛物线于点D,试判断以点A为圆心,AD的长为半径的圆与y轴的位置关系,并给出证明;(3)设直线x=3与直线BD相交于点G,与x轴交于点N,问:在⊙A上是否存在一点Q,使△QOG的面积最大?若存在,求出△QOG面积的最大值;若不存在,请说明理由。
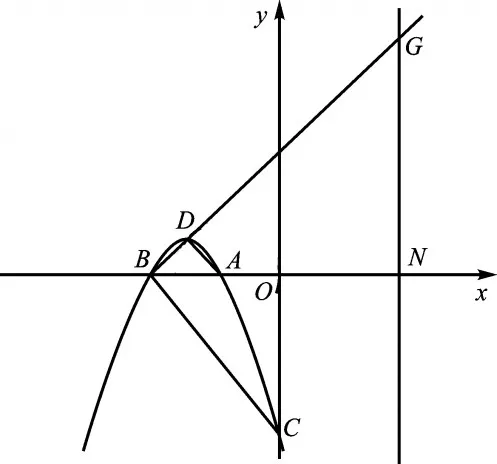
图8
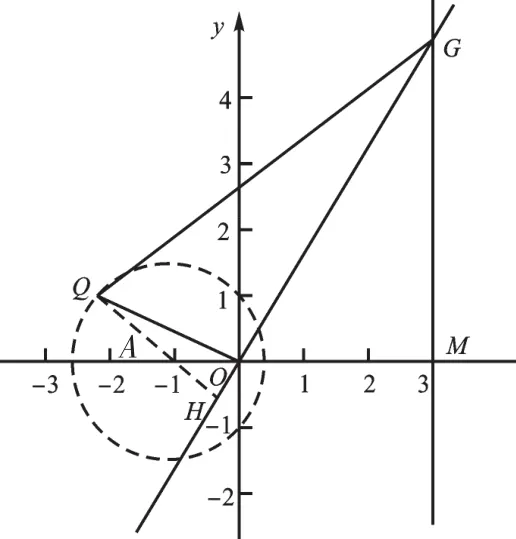
图9
思路突破:(1)结合A,B点的坐标,可以设出交点式y=a(x+1)(x+3),再根据OA∶OC=1∶3可得点C的坐标(0,-3),于是代入“交点式”,可得a=-1,即a=-1,b=-4,c=-3。
(2)结合B,C点的坐标可得直线BC的解析式为y=-x-3,而经过点B且垂直于BC的直线BD解析式是y=x+3,将它与抛物线解析式联立成方程组,可得D(-2,1)。
而将抛物线解析式配方成顶点式y=-(x+2)2+1,可确认它的顶点是(-2,1)。即点D就是抛物线的顶点,于是AD=2,也就是圆A的半径是2,而点A到y轴的距离是1,故圆A与y轴相交。
(3)首先思考圆上一点与O、G围成的三角形,OG长35,若OG边上高最大时,△QOG面积就取得最大。如图9,如果想到过A点作OG的垂线,交圆A于第二象限内的点Q,交直线OG于H点,则△QOG面积最大。接下来的关键是求出QH的长,我们将QH分成两个部分来思考,一是半径AQ(上一问已求出),二是AH。可以在Rt△AOH中思考,利用△AOH∽△GOM,可以得到,此时△QOG面积的最大值为
“形异质同”的反思:上述两道试题看似“风马牛不相及”,然而在分析最值时都涉及一种经验,即过圆内一点到圆上任意一点的连线段中,以经过圆心时为最长。如图10,点A到圆上任意一点的连线段中,经过圆心O的线段AB最长,相应地,我们还可得出此时AC是最短的。

图10
二、解题研究与教学思考
1.重视同类考题的归类整理,积累同类题服务教学。
不少有经验的教师都有自己的个性化教学素材,特别是会在电脑中分类整理一些专题素材,比如一些同类考题能及时归类存档,挖掘出图10这样的深层结构,便于随时调用。在组织习题讲评、专题复习、编制相关学案时,能很方便地检索出相关试题,有时只要简单改编或链接一下,就能使得讲评课“增色”不少,很有深度。
2.引导学生辨析“形异质同”题,做一题、会一类、通一片。
教师善于积累同类考题的一个好处就是,当预设讲评某一类型的较难试题时,在讲评之后可以及时链接同类考题(这就启示我们平时应注意收集能体现图10这样结构的素材),让学生在两道同类试题解答之后辨析“形异质同”试题,使得他们识别“形异质同”题的“眼力”更强,可以达到做一题、会一类、通一片的解题效果。
3.向学生传递回顾反思意识,学会整理自己的学习笔记。
教师在讲评较难试题时,如果能及时安排解后回顾反思的教学环节,不但能使学生获得更深刻的理解,也能让理解较慢的学生获得更多的时间进行“消化”,同时也是向学生传递解后回顾反思的意识。根据教学经验,我们发现不少优秀的学生,总是能将平时练习、教师链接讲评的一些同类考题及其结构归类整理成他们个性化的学习笔记,有些甚至还及时整理成反思类的数学写作,这些都可看成是促进自身深刻理解同类习题的一种有效措施。
此外,根据个人命题兴趣,提出两点命题建议。考题1是生活应用问题,叙述冗长,因学生缺少类似的生活场景、生活常识,可能并不知道考题的设计意图、求解方向,理解题意有些困难,这与“好的试题”追求简洁好懂、指令明确的高要求相比,还有一定的距离,作为时间紧、任务重的中考试卷,建议慎考这样的阅读量过大、理解题意困难的考题;考题2是一道“伪坐标系”考题,特别是最后一问的最值探究与抛物线毫无关联,让题干过早地“枯萎”、无效,这也是一种值得商榷的命题方式。
(作者为江苏省如东县洋口镇古坳初级中学教师)
[1]储秀梅.同类跟进:试卷讲评课的一种策略——以一道反比例函数把关题讲评为例[J].中学数学,2017(5初中):61-62.
[2]沈丽婧.聚焦微专题:中考二轮复习的实践与思考——以一组“关联试题”复习为例[J].中学数学,2017(3初中):36-37.



