文黄海涛
(作者单位:江苏省无锡市滨湖中学)
直线与圆的位置关系共有三种:相离、相切、相交,其中相切作为一种最特殊的位置关系,是本章研究的重点,往往也是考查的重点和难点。在解决一些与圆有关的相切问题时,常用的知识有切线的性质及其判定定理,但通常都需要添加辅助线,把切点和圆心连接起来,构造半径,我们称之为“见切点,连半径”。
一、“连半径”,解决与切线有关的计算问题
例1 如图1,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E。若AD=8,DE=5,求BC的长。

图1
【分析】由DE为⊙O的切线,容易想到连接半径OD,如图2,得到∠ODE=90°。利用同角的余角相等,可得∠ADE=∠A,进而推出AE=DE,考虑条件∠C=90°,比较容易看出C为⊙O的切点,得到CE=DE。此时结合条件,边长AD、AC都可以确定,进一步考虑连接DC构造直角三角形ADC,求出CD,继而在直角三角形BDC、ABC中利用方程解决问题。

图2
【简解】如图2,连接OD,证明∠A+∠B=90°,由△BDO为等腰三角形推出∠ADE+∠B=90°,得到结论∠ADE=∠A,进而得到结论AE=DE。连接DC,由∠C=90°,可证明EC为⊙O的切线,得结论CE=DE。结合条件数值求得AC=2DE=10,由BC为直径,得在直角三角形ADC中,DC=6,设BD=x,在直角三角形BDC中,BC2=x2+62,在Rt△ABC中,BC2=(x+8)2-102,可得 x2+62=(x+8)2-102,解方程 x=由勾股定理得BC
【归纳】本题考查了切线的性质、勾股定理、等腰三角形的判定和性质等知识。解题的关键是连接半径,得到垂直的同时还构造出了等腰三角形,进而得出角相等、线段相等,这才有了后面一系列的转化。因此与切线有关的计算问题,“连半径”往往是解决问题的起点与关键,也是解决后续问题的基础,要把连接半径后的结论细细梳理。
二、“连半径”,解决与切线有关的证明问题
例2 (2019·滨州)如图3,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC,垂足为点F。
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CF·AC。
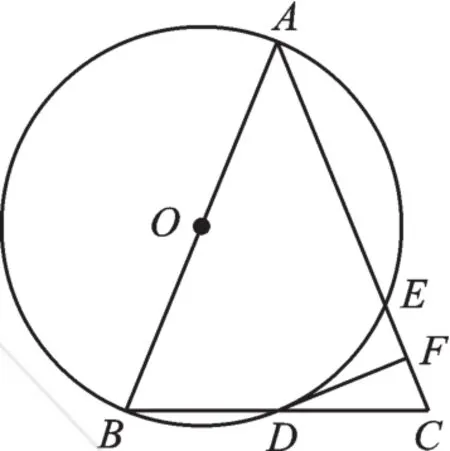
图3
【分析】(1)证明DF是⊙O的切线,题目信息中已明确D为圆上的点,连半径,证垂直即可;
(2)由结论BC2=4CF·AC可知,本题的落脚点应该放在三角形相似上,关键是对数字“4”如何处理?考虑到前面的平方,联想到BC与DC有两倍关系,连接AD,证明△CFD∽△CDA,尝试推导结论得证。
【简解】(1)如图4所示,连接OD,由AB=AC,得出∠ABC=∠C,而OB=OD,得出∠ODB=∠ABC=∠C,因为DF⊥AC,所以∠CDF+∠C=90°,进而得到∠CDF+∠ODB=90°,∠ODF=90°,得出结论——直线DF是⊙O的切线;
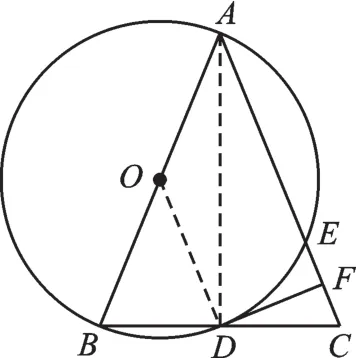
图4
(2)连接AD,则AD⊥BC,由AB=AC,
【归纳】在证明圆的切线时,把该直线与圆的交点和圆心连接起来,证明半径垂直于该直线即可,我们称之为“连半径、证垂直”;反之,当已知切线时,把切点和圆心连接起来,可以得到半径与切线垂直。



