最大似然估计法的思想及其应用

李 娜 于晓要

（商丘工学院基础教学部，河南 商丘 476000）

1 引言

在数理统计中，参数估计是统计推断的基本问题之一.当总体的分布类型已知，但含有一个或多个未知参数时，如何求出未知参数的估计值或估计出未知参数的取值范围的一类问题，即是参数估计问题.参数估计一般有两种形式：其一是通过总体的一组样本X1,X2,… ,Xn所提供的信息，来求出未知参数θ的估计值，这就是一类点估计问题；其二是通过样本寻求一个区间使它有一定的把握包含被估的参数，此类即为区间估计问题.求点估计的方法很多，最常用的是矩估计法与最大似然估计法.本文介绍最大似然估计法的基本思想及其应用.

2 最大似然估计法的思想及其应用

最大似然估计法是参数点估计中一种重要方法，它的思想是由着名数学家高斯提出，后被统计学家费希尔（R.A.Figher）于1912年在一项工作中应用并得到证明.

最大似然估计法的直观想法是：在条件未知的随机试验中，如果某事件已经发生，则根据事件发生的概率最大原则去推断试验条件。即：在已经得到试验结果的条件下，应该寻找使这个结果出现的概率最大的那个估计作为总体未知参数的估计。

若总体X属离散型，其分布律P{X=x}=p(x;θ)，θ∈Θ的形式为已知，θ为待估参数，Θ是θ可能取值范围.设X1,X2,… ,Xn为来自总体X样本，则X1,X2,… ,Xn的联合分布律为

又设x1,x2,… ,xn是相应于样本X1,X2,… ,Xn的一个样本值.易知样本取到观察值x1,x2,… ,xn的概率，亦即事件发生的概率为

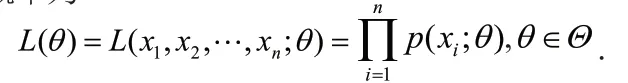
这一概率随θ的取值而变化，它是θ的函数，L(θ)称为样本的似然函数（这里x1,x2,… ,xn是已知的样本值，它们都是常数）.

若总体X属连续型，其概率密度f(x;θ)，θ∈Θ的形式为已知，θ为待估参数，Θ是θ可能取值范围.设X1,X2,… ,Xn为来自总体X样本，则的联合密度为即为样本的似然函数L(θ).

于是求总体参数θ的最大似然估计值，就转化为求似然函数L(θ)的最大值问题.因此当L(θ)关于θ可微时，常可从方程解得.又因L(θ)与lnL(θ)在同一处取到极值，因此，θ的最大似然估计也可从方程求得，而后一方程求解往往比较简便.称为对数似然方程.结合以上分析，我们可得到求最大似然估计的步骤：

例1 设总体X服从参数为λ的泊松分布，其中λ＞0为未知参数，是来自总体X的样本，求参数λ的最大似然估计量.

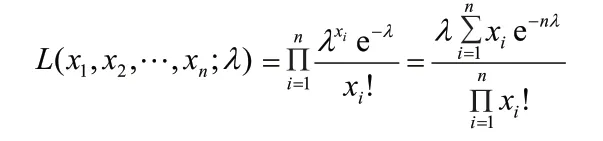
关于λ求导，并令其为0，即

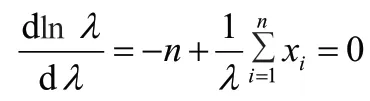
解得λ的最大似然估计值，

λ的最大似然估计量，

最大似然估计法也适用于分布中含多个未知参数θ1,θ2,…,θk的情况.这时，似然函数L是这些未知参数的函数.分别令

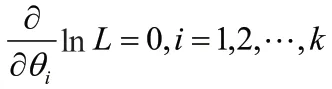
解上述k个方程组，即可得到各未知参数的最大似然估计值.

例2 设X～N(μ,σ2)，μ,σ2均为未知参数，x1,x2,… ,xn是来自总体X的样本值.求μ,σ2的最大似然估计量.

解X的概率密度为

似然函数为

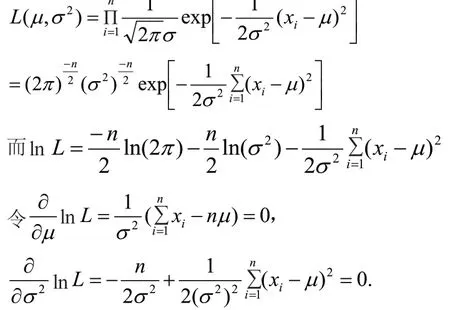
3 结束语

最大似然估计法是参数点估计中一种重要方法，它是在已经得到试验结果的条件下, 应该寻找使这个结果出现的概率最大的那个参数值作为总体未知参数的估计值.在一定条件下，只要样本容量足够大，最大似然估计与待估的未知参数的真值可相差任意小，最大似然估计法是较理想的估计方法.