文封霞霖
(作者单位:江南大学附属实验中学)
直线与圆的位置关系有三种:相离、相切、相交,其中相切是中考的高频考点。我们对直线与圆的位置关系的研究,反映了图形的位置关系与相应的数量关系之间的内在联系:由图形的位置关系决定数量关系,由数量关系判定图形的位置关系。这里的数形结合,既是重要的知识内容,又是重要的思想方法。
一、切线与函数
例1 (2019·菏泽)如图1,直线y=-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是____。
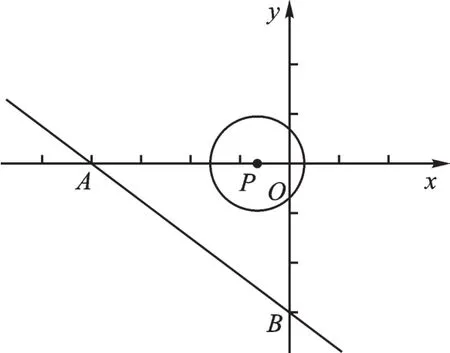
图1
【分析】考点:一次函数、切线性质。对于运动问题,要考虑多解。对圆心位置分类讨论,圆心在A点左侧和右侧,直线都会与圆相切。根据相切时圆心到直线的距离等于半径,结合相似或者三角函数,找到圆心P的位置。
解:∵直线交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(-4,0),B(0,-3),
∴OA=4,OB=3,∴AB=5。
设⊙P与直线AB相切于D,连接PD,如图2,P在A点左侧时为P1,在A点右侧时为P2。
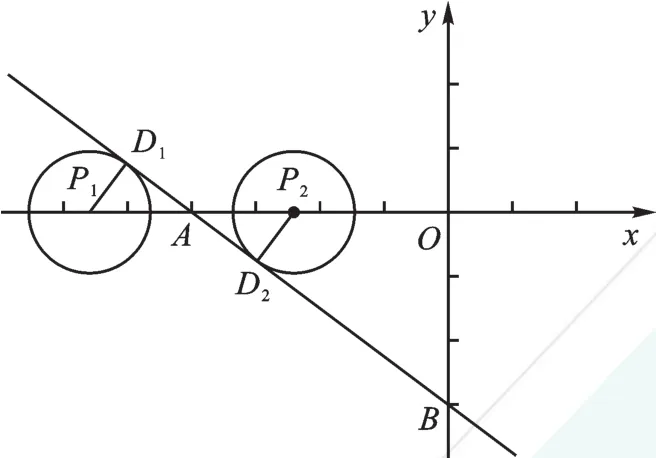
图2
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,
∠PAD=∠BAO,
∴△APD∽△ABO,
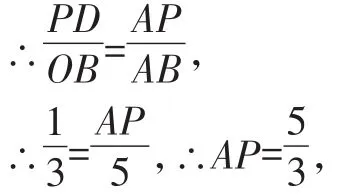
∴OP=OA+AP或OA-AP,

【点评】这道题目中有圆,但要做到心中无圆。如果抓住切线的本质,⊙P1和⊙P2不画出来亦可。我们要抓住的关键是直线与圆相切时,圆心到直线的距离等于半径。另外,利用相似求AP的这部分,用三角函数也可以解决。
二、切线与角度
例2 (2019·天津)已知PA,PB分别与⊙O相切于点A、B,∠APB=80°,C为⊙O上一点。

图3
(Ⅰ)如图3-①,求∠ACB的大小;
(Ⅱ)如图3-②,AE为⊙O的直径,AE与BC相交于点D,若AB=AD,求∠EAC的大小。
【分析】考点:切线的性质、圆周角定理、等腰三角形的性质。掌握圆的切线垂直于经过切点的半径是解题的关键。(Ⅰ)连接OA、OB,根据切线的性质得到∠OAP=∠OBP=90°,再根据四边形内角和等于360°计算;(Ⅱ)连接CE,根据圆周角定理得到∠ACE=90°,根据等腰三角形的性质、三角形的外角性质计算即可。
解:(Ⅰ)如图4,连接OA,OB。

图4
∵PA,PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
即∠OAP=∠OBP=90°。
∵∠APB=80°,
∴在四边形OAPB中,∠AOB=360°-∠OAP-∠OBP-∠APB=100°。
∴∠ACB=50°。
(Ⅱ)如图5,连接CE。
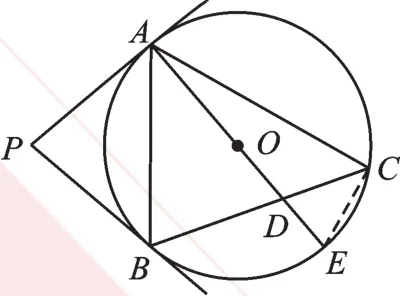
图5
∵AE为⊙O的直径,∴∠ACE=90°。由(Ⅰ)知,∠ACB=50°,
∴∠BCE=∠ACE-∠ACB=40°,
∴∠BAE=∠BCE=40°。
∵在△ABD中,AB=AD,
又∠ADB是△ADC的一个外角,有∠EAC=∠ADB-∠ACB,
∴∠EAC=20°。
【点评】在圆中求角度,通常考虑“由角找弧,再由弧找角”,熟练地转化圆周角和圆心角。在第(Ⅱ)题中,求∠BAE的度数,也可以连接OB,利用等腰三角形的性质求解。
三、切线与特殊三角形
例3 (2019·盐城)如图6,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的⊙O分别交AC、BC于点M、N,过点N作NE⊥AB,垂足为E。
图6
(2)求证:NE与⊙O相切。
【分析】考点:切线、勾股定理、直角三角形斜边上的中线等于斜边的一半、等腰三角形“三线合一”、中位线性质。本题需要添加辅助线,构造过切点的半径和直径所对的圆周角。
(1)解:连接ON、DN,

图7
∵CD是Rt△ABC斜边上的中线,
∵Rt△ABC中,∠ACB=90°,AB=10,AC=6,∴BC=8。
∵CD为直径,∴∠CND=90°。
∵在△BCD中,
BD=CD,∠CND=90°,

(2)证明:∵O,N为CD,BC的中点,
∴ON∥BD,∴∠ONE+∠DEN=180°,
∵∠DEN=90°,
∴∠ONE=90°,即ON⊥NE,
又∵ON为半径,
∴NE与⊙O相切。
【点评】本题以圆的切线为主线,综合考查了特殊三角形的性质。三角形是几何的根本,特殊三角形的性质也是中考必考知识点。
四、切线与三角函数
例4 (2019·济宁)如图8,AB是⊙O的直径,C是⊙O上一点,D是⁀的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F。

图8
(1)求证:AE是⊙O的切线;
【分析】(1)根据“三线合一”得到OE⊥AC,求得∠AFE=90°,再转化为∠EAO=90°;
(2)根据等弧对等角、相等的角三角函数相等,将已知条件一步步转化为结论。
(1)证明:连接OC,如图9。

图9
∴∠AOD=∠COD,
又∵OA=OC,
∴OE⊥AC,
∴∠AFE=90°,
∴∠E+∠EAF=90°,
∵∠AOE=2∠ACD,∠CAE=2∠ACD,
∴∠CAE=∠AOE,
∴∠E+∠AOE=90°,
∴∠EAO=90°,
又∵OA为半径,
∴AE是⊙O的切线。
(2)解:连接AD,
∵AB为直径,
∴∠ADB=90°。
∴∠DAH=∠ACD,
∴在Rt△ADH中,

∵DH=9,∴AD=12。
∵∠B=∠ACD,
∴BD=16,
∴在Rt△ADB中,AB=20。
【点评】本题考查了切线的判定、圆周角定理,转化思想是解题的关键。



